Преобразования Лоренца

Верность преобразований Галилея вроде бы не должна подвергаться сомнениям. Ведь в нашей каждодневной жизни мы, По-существу, очень часто пользуемся ими, естественно не отдавая себе в этом отсчета.

Действительно, если мы очень торопимся, то идем или бежим по эскалатору. И тогда к скорости движения эскалатора прибавляется скорость нашего собственного движения относительно него. Если вы бежите по движущейся беговой дорожке и скорости вашего бега и движения дорожки равны численно и противоположно направлены, то относительно спортзала вы не перемещаетесь. И еще существует бесконечно много процессов, которые описываются с помощью преобразований Галилея.

А теперь немного пофантазируем. Представим, что мы летим в космическом корабле (фотонная ракета!) и после многих лет полета по межзвездным просторам приближаемся к планетной системе какой-то звезды со скоростью почти равной скорости света (V» с = 3×10⁸ м/с). Локационная установка корабля испускает электромагнитный импульс, который распространятся со скоростью света, u ¢ = с =3×10⁸ м/с.

Тогда, в соответствии с формулой (41) скорость движения электромагнитного импульса относительно звезды должно составлять:

u = u ¢ + V»3×10⁸ + 3×10⁸» 6×10⁸ м/с» 600000 км/с.

А этого, оказывается, не может быть. Еще в 80-х годах XIX века американский физик Альберт Абрахам Майкельсон (1852-1931, Нобелевская премия 1907 г.) опытным путем доказал независимость скорости света в вакууме от движения источника. Говоря по-другому – скорость света в вакууме не зависит от выбора инерциальной системы отсчета и составляет, по современным данным, 299792458 м/с (»3×10⁸ м/с).

Следовательно, электромагнитный импульс, пущенный с космического корабля в «нашем межзвездном перелете» должен идти к звезде со скоростью с = 3×10⁸ м/с.

Полученное противоречие свидетельствует о том, что преобразование Галилея в данном случае неприменимы.

При скоростях движения соизмеримых со скоростью света (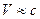) используются формулы, называемые преобразованиями Лоренца (Людвиг Валентин Лоренц (1829-1891) – датский физик-теоретик. Нобелевская премия 1902 г).

Вид преобразований Лоренца при условии движения только вдоль оси x (см. п. 9.1) следующий:

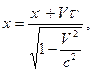y=y ¢, z=z ¢.

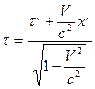, (43)

где с - скорость света в вакууме; x, y; z, x ¢, y ¢, z ¢,t, t¢ - имеют тот же смысл, что в (34).

Одно из кардинальных отличий формул (43) от формул (36) заключается в том, что время (t) оказывается величиной, зависящей от координат. Таким образом, следует говорить не об изменении пространственных координат, скорости и т.п. со временем, а о пространственно-временных координатах, т.е. о четырех координатах пространства - времени.

При скоростях движения значительно меньших скорости света (V<< c), знаменатель в формулах (43) практически равен единице и вид этих формул становится таким же, как (34). Таким образом, преобразования Галилея верны только при движении с очень малыми по сравнению со скоростью света скоростями.

Для скоростей V> c преобразования Лоренца теряют смысл (подкоренное выражение меньше нуля). Следовательно, материальные объекты не могут двигаться со скоростями большими скорости света.

9.3. Неодновременность «одновременных» событий.

Из независимости скорости света от движения системы отсчета вытекают весьма странные, с обыденной точки зрения, следствия.

Представим, что на некотором расстоянии от неподвижного наблюдателя (система отсчета) вспыхивают две лампочки. Если наблюдатель видит эти вспышки одновременно, то считается, что и сами события (вспышки) произошли одновременно в разных точках пространства (рис. 15).

Действительно, так как расстояния от источников света Л₁ и Л₂ до наблюдателя одинаковы (l ₁ = l ₂) и скорость распространения сигнала (скорость света) от обоих источников одинакова, то интервалы времени Dt₁ и Dt₂, необходимые для прохождения светом отрезков l ₁и l ₂ от ламп Л₁ и Л₂ будут равны (Dt₁ = Dt₂).

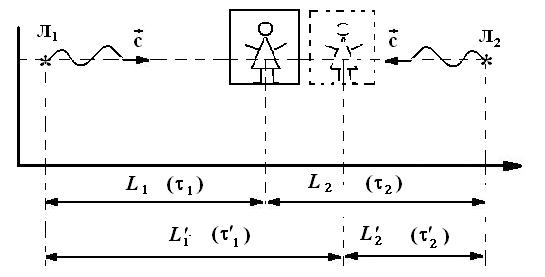
Рис.15. К неодновременности одновременных событий

Пусть теперь наблюдатель движется по направлению от источника Л₁ к источнику Л₂. Скорость распространения сигналов от Л₁ и Л₂ до наблюдателя по-прежнему одинакова. Но за то время пока свет от источников доходит до наблюдателя, последний смещается на расстояние D l. Тогда свет от Л₁ проходит до наблюдателя расстояние l ₁¢ = l ₁ + D l, а от Л₂ ¾ l ₂¢= l ₂ - D l, Понятно, что l ₁¢ > l ₂¢, а значит время Dt₁¢, за которое свет доходит от источника Л₁ до наблюдателя больше времени Dt₂¢ движения сигнала Л₂ до наблюдателя (Dt₁¢ > Dt₂¢).

Таким образом, в этом случае наблюдатель увидит вспышки не одновременно, но раньше вспышку Л₂, позже - Л₁. Вспышки ламп Л₁ и Л₂, произойдут для него не одновременно, следовательно, события одновременные в одной инерциальной системе отсчета оказываются неодновременными в другой.

Дата добавления: 2014-12-27