Теоретическая часть

Последовательность выполнения работы

ТОПОГРАФИЧЕСКИЕ КАРТЫ

Цель работы

Приобрести навык в работе с топографической картой при решении по ним инженерно- геодезических задач.

Приборы и принадлежности: учебная топографическая карта, масштабная линейка, транспортир, циркуль-измеритель, листы миллиметровой бумаги и кальки.

1) Измерение расстояний при помощи нормального поперечного масштаба.

2) Определение прямоугольных координат точек.

3) Определение углов ориентирования линии, заданной на карте.

4) Определение высот точек.

5) Построение на топографической карте линии с заданным предельным уклоном.

6) Построение профиля местности по заданному направлению.

1) Измерение расстояний при помощи нормального поперечного масштаба.

При решении задач по топографической карте для измерений с повышенной точностью применяют поперечный масштаб. Поперечный масштаб представляет собой график, основанный на пропорциональным делении отрезков (рис.16).

На горизонтальной прямой несколько раз отложен отрезок CD – основание масштаба. Из полученных точек на прямой восстановлены перпендикуляры. Через промежутки, равные 0,1 CD, на перпендикулярах проведены 10 прямых линий. Эти прямые параллельны горизонтальной линии.

Крайнее левое основание снизу и сверху разделено на 10 частей. Таким образом, одно деление левого основания соответствует 0,1 CD. Полученные точки соединены наклонными линиями - трансверсалями.

Параллельные прямые, пересекаясь с трансверсалью делят её на 10 равных отрезков. Проекция каждого из этих отрезков на основание масштаба равна 0,1 части минимального деления и является 0,01 частью основания масштаба (рис.15). Следовательно,номер горизонтальной прямой- есть число сотых долей основания.

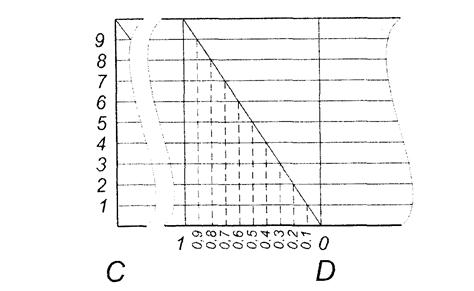
Рис. 15. Проекция отрезков на основание масштаба.

Для удобства пользования поперечные масштабы строятся с разными основаниями, в зависимости от масштаба топографической карты.

Масштабы топографических карт и величины соответствующих им именований поперечных масштабов приведены в табл. 10.

Таблица 10

Масштабы топографических карт и соответствующие им

основания поперечных масштабов

Масштабы топографических карт	Основания поперченных масштабов см.
1: 10 000; 1: 100 00; 1: 1000 000
1: 200 000
1: 25 000
1: 50 000; 1: 500 000

Поперечный масштаб с основанием 2 см называется нормальным

Порядок измерения расстояний:

• Выяснить, каким расстояниям на местности соответствуют основные деления поперечного масштаба. Например, для карты масштаба 1:50000 основные деления поперечного масштаба 2см, 2мм и 0,2мм соответствуют 1000м, 100м и 10м.

• Взять в раствор циркуля измеряемое расстояние. Перенести его на поперечный масштаб так, чтобы правая игла совпадала с одним из перпендикуляров правее нуля. Передвигая вверх по перпендикуляру ножку циркуля, совместить левую иглу с одной из трансверсалей. Необходимо следить за тем, чтобы обе ножки циркуля располагались на одной прямой, параллельной основанию.

• Отсчёт количества целых оснований делать по правой игле циркуля.

• Отсчёт десятых долей основания- по наклонной прямой, на которой стоит левая игла.

• Сотые доли отсчитываются по числу вертикальных делений между горизонтальной линией, на которой стоит циркуль, и основанием масштаба.

Рис. 16. Поперечный масштаб

Например, расстояние между точками A и B (рис.16) для карты масштаба 1: 50 000 равно 2 560 м:

S_АВ = 2000 + 500 + 60 = 2560 м.

2). Определение прямоугольных координат точек.

На листе топографической карты нанесена сетка прямоугольных координат Гаусса – Крюгера. Километровая координатная сетка представляет собой сеть квадратов, образованных прямыми линиями, параллельными осевому меридиану зоны и экватору. Координатная сетка называется километровой, т.к. прямые линии проведены через целое число километров. Ближайшие к углам рамки линии координатной километровой сетки подписываются полным числом километров, а остальные – двумя последними цифрами.

Порядок определения прямоугольных координат точки:

• по оцифровке определить значения координат (х _0, у ₀) юго- западного угла квадрата, в котором расположена заданная точка;

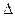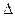• с помощью циркуля- измерителя и поперечного масштаба измерить длины перпендикуляров, опущенных из точки на заданную и южную стороны квадрата координатной сетки; полученные значения х и у

- есть приращения координат;

• координаты точки вычислить по формулам:

х_А = х_о + 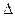х

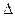y_А= у_о+ у.

Например, для точки А ( рис.17) измеренные значения координат будут следующими:

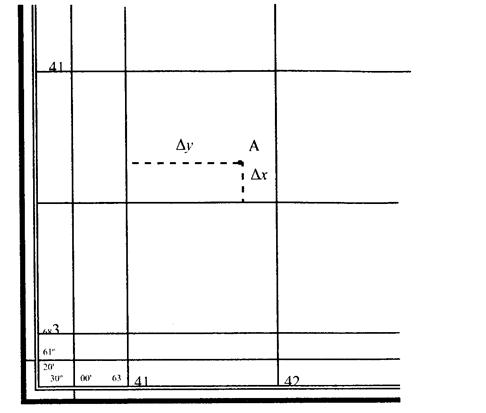
Рис. 17. Измерение значений координат для точки А

Х_{А =} 6840000 + 300 = 6840300 м;

У_А = 6341000 + 800 = 6341800 м.

3). Определение углов ориентирования линии, заданной на карте.

Ориентировать линию- это значит определить угол ориентирования между направлением данной линии и направлением, принятым за исходное.

Углы ориентирования различают в зависимости от принятого исходного направления.

Принятые в геодезии исходные направления, названия углов ориентирования и их обозначения приведены в табл. 11.

Таблица.11

Исходные направления и соответствующие им углы ориентирования

Номер n/n	Исходное направление	Название угла   ориентирования	Обозначение
	Северное направление осевого меридиана зоны (ось Х) или линии ему параллельной     Северное направление истинного(географического) меридиана   Северное направление магнитного меридиана     Ближайшее северное или южное направление меридиана	Дирекционный угол   Истинный (географический) азимут     Магнитный азимут   Румб	a   А     Ам   r

Дирекционный угол и азимут отсчитывают от меридиана по направлению часовой стрелки. Они принимают значения от 0^о до 360^о.

Румб изменяется от 0^о до 90^о. Перед числовым значением румба указывают название четверти: СВ(северо-восток), ЮВ (юго-восток), ЮЗ (юго-запад), СЗ (северо-запад). В зависимости от исходного меридиана различают истинный, магнитный и дирекционный румбы.

Так как на топографическую карту нанесена координатная сетка, а образующие её вертикальные линии параллельны осевому меридиану зоны, то для ориентирования линии по карте наиболее удобно измерить дирекционный угол (рис.18,а).

Порядок измерения дирекционного угла:

• Если линия не пересекает вертикальной линии координатной сетки, продолжить её до пересечения с ближайшей вертикальной координатной линией;
• При измерении дирекционного угла, имеющего величину от 0^о до 180^о, нулевой радиус транспортира совместить с северным направлением вертикальной координатой линии;

• Для углов, больше 180^о, нулевой радиус транспортира совместить с южным направлением. К полученному отсчёту прибавить 180^о.

Вычисление углов ориентирования.

• Истинный азимут вычислить по формуле

А_и= a+-y,

где a – измеренное значение дирекционного угла;

у – среднее значение угла сближения меридианов для данного листа карты

(восточно – положительное, западное – отрицательное).Указывается на диаграмме взаимного расположения осевого, истинного и магнитного меридианов (рис.18,б).

• Магнитный азимут вычислить по формуле

А_м = А_и +- b

где b – склонение магнитного меридиана (восточное – положительное, западное – отрицательное). Указывать на диаграмме под южной рамкой карты (рис. 18,б).

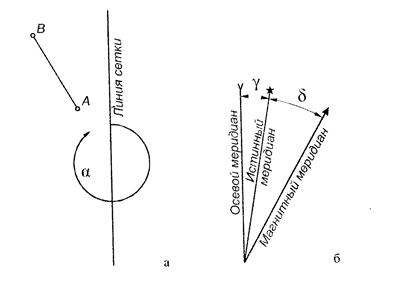
Рис. 18. Дирекционный угол и диаграмма расположения осевого, истинного и магнитного меридианов

• Связать между соответствующими азимутами и румбами:

СВ :r =А;

ЮВ ::r= 180^о – А;

ЮЗ: r =А – 180^о;

СЗ: r =306 ^о– А.

Пример вычисления

Пусть a = 327^о45,

Тогда

А_и=a-у= 327^о 45’- 2^о 21’= 325^о 24’;

А_и=А-б = 325^о 24’- 6 ^о15’ = 319^о 09’,

если б = 6^о 15’, а у = 2^о 21’.

В зависимости от исходного направления румбы принимают значения

СЗ: r = 360^о00’ – А = 360^о 00 – 327^о 45’ = 32^о 15’;

СЗ: r _и= 360^о 00’ – А _и = 360^о 00 ‘– 325^о 24’ = 34^о 36’.

СЗ: r _м = 360^о00’ – А _м = 360^о 00’ –319 ^о09’ = 40^о 51’.

4). Определение высот точек

Рельеф на топографических картах изображают горизонталями. Горизонталь – линия, соединяющая точки земной поверхности с одинаковыми высотами.

Определение высоты точки по карте зависит от её положения относительно горизонталей.

Если точка расположена на горизонтали, тогда её отметка равна отметки горизонтали. Например на рис. 19 точка Е лежит на горизонтали с отметкой Н = 251м, тогда

Н_Е = 251м.

Если точка расположена между горизонталями с отметками Н₁ и Н₂, тогда её отметку можно определить интерполированием. Для этого:

• Через точку провести линию, перпендикулярную горизонталями(рис.19);

Рис. 19. Определение высоты точки

• Измерить с помощью поперечного масштаба расстояния d₁ и d₂ между точкой и ближайшими горизонталями;
• С учётом направления ската местности отметку Н _С точки вычислить дважды по формулам:

;

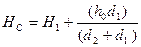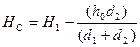
Где h_о –высота рельефа.

• За окончательное принять среднее арифметическое из вычисленных отметок.

5). Построение на топографической карте линии с заданным предельным уклоном.

Расстояние между соседними горизонталями на плане заложением а. Крутизной ската называется угол наклона ската v. Уклоном i линии называется отношение превышения h к горизонтальному проложению d.

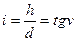
Провести на карте между точками А и В линию заданного предельного уклона – это значит провести между данными точками кратчайшую линию так, чтобы ни один отрезок не имел уклона больше заданного предельного .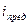

Для этого необходимо определить по графику заложений величину заложения 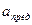. График заложений помещен под южной рамкой карты. На горизонтальной оси отложены значения углов наклона в градусах 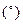или значения уклонов в промилле 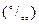, а на перпендикулярах – соответствующие им значения заложений в масштабе карты. Концы перпендикуляров соединены плавной кривой.

Определение величины заложения

• Из точки горизонтальной оси, соответствующей значению заданного уклона, восстановить перпендикуляр до его пересечения с кривой линией графика (рис.20). длина полученного отрезка соответствует величине заложения. Его численное значение можно получить по поперечному масштабу.

• Если на топографической карте не приведен график заложения, тогда заложение 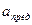можно вычислить по формуле

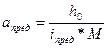
где М – знаменатель численного масштаба карты.

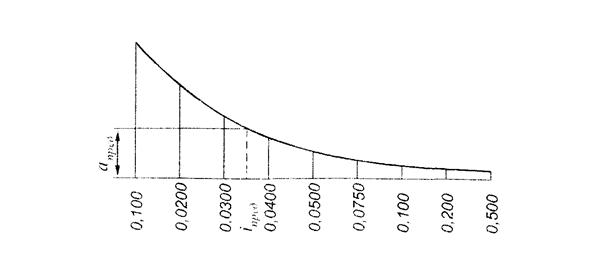
Рис. 20. Определение величины заложения

Порядок проведения по карте линии с заданным предельным уклоном:

• Соединить на карте точки А и В прямой линией;

• Взять в раствор циркуля отрезок, соответствующий заложению ;

• Из точки А в направлении к точке В раствором циркуля засечь на соседней

• горизонтали точку l; затем точки l тем же раствором циркуля засечь точку на следующей горизонтали и т.д.;

• Если раствор циркуля меньше расстояния между горизонталями, то линию провести по кратчайшему расстоянию;

• Соединить все точки на горизонталях.

Ломаная линия (рис. 21), построенная вдоль направления АВ, - есть линия с уклоном, не превышающим заданного.

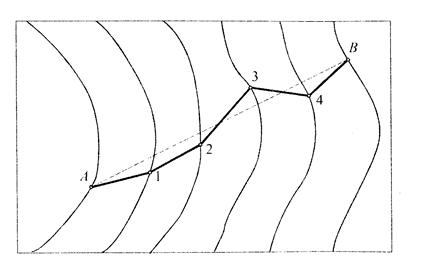
Рис. 21. Линия с уклоном, не превышающим заданного.

6). Построение профиля местности по заданному направлению.

Профилем называется уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного направления. Профиль местности строят в масштабе карты.

Порядок построения

• Соединить на карте точки А и В прямой линией. Пронумеровать точки пересечения линии с горизонталями, а также характерные точки (точки пересечения линии с водосливом и водоразводом).

• Перенести в нижнюю часть листа миллиметровой бумаги линию АВ в масштабе карты и отложить на ней пронумерованные точки. Линия АВ служит основанием профиля.

• От линии АВ начертить профильную сетку, состоящую из двух горизонтальных граф (рис.22).

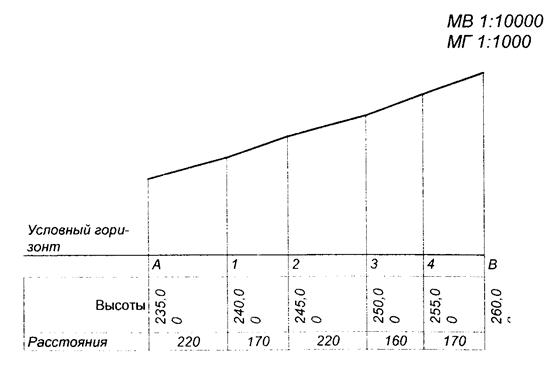
Рис. 22. Построение профиля местности

• Вертикальный масштаб взять в 10 раз крупнее горизонтального. Например, если горизонтальный масштаб 1: 2 000, тогда вертикальный масштаб 1: 200.

• Верхнюю линию профильной сетки (линию АВ) принять за условный горизонт. Отметку условного горизонта выбрать так, чтобы нижняя точка местности на профиле отстояла от линии условного горизонта на расстоянии больше 1см.

• От линии условного горизонта в каждой точке построить перпендикуляры. На перпендикулярах отложить в выбранном масштабе разности отметок 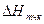между отметками 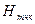и отметкой условного горизонта 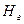, т.е.

.

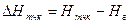• Концы перпендикуляров соединить плавной кривой, которая будет изображать профиль местности.

• В графу профильной сетки «отметки» вписать значения отметок точек пересечения профильной линии с горизонталями, а также характерных точек местности. В графу «горизонтальные расстояния» вписать значения горизонтальных проложений отрезков на местности

S = s*M,

где s – длина отрезка на плане,

М – знаменатель численного масштаба.

Дата добавления: 2014-12-27