
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дизъюнктивные и конъюнктивные нормальные формы. Полином Жегалкина. Двойственные и самодвойственные функции. 1 страница
|
|
|
|
Основные элементарные булевы функции. Основные свойства. Существенные и фиктивные переменные. Способы задания.
Функции алгебры логики.
Часть 1
Опр1. Функция  , определенная на множестве
, определенная на множестве 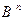 и принимающая значения из
и принимающая значения из
множества {0,1}, называется функцией алгебры логики или булевой функцией.
Множество всех булевых функций обозначается  .
.
Элементарные булевы функции:
- одной переменной:
1.  - нуль функция; 2.
- нуль функция; 2. 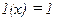 - единичная функция;
- единичная функция;
3. 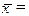 {
{ 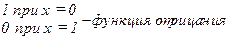 ; 4.
; 4. 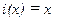 - тождественная функция;
- тождественная функция;
Таблица 1.
| x | 0 | 1 | x | 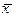
|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
-двух переменных:
5. 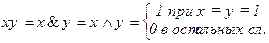 6.
6. 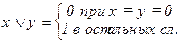
7. 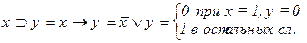 8.
8. 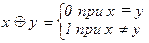
9. 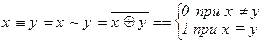 10.
10. 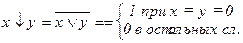
11. 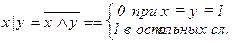 12.
12. 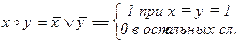
Функциональные символы:
& - конъюнкция; V - дизъюнкция; 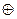 - сумма по модулю 2; ~ - эквивалентность;
- сумма по модулю 2; ~ - эквивалентность; 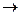 - импликация;
- импликация; 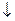 - стрелка Пирса; | - штрих Шеффера;
- стрелка Пирса; | - штрих Шеффера; 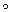 - функция Вебба.
- функция Вебба.
Основные свойства элементарных функций:
1. Коммутативность:
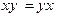 ;
; 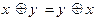 ;
;  ;
; 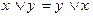 ;
; 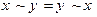 ;
; 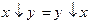 .
.
2. Ассоциативность:
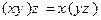 ;
;  ;
; 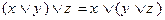 ;
;
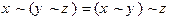 .
.
3. Дистрибутивность:
 - конъюнкция относительно дизъюнкции;
- конъюнкция относительно дизъюнкции;
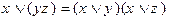 - дизъюнкция относительно конъюнкции;
- дизъюнкция относительно конъюнкции;
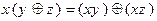 - конъюнкция относительно смещения по модулю 2.
- конъюнкция относительно смещения по модулю 2.
4. Принципы де Моргана:

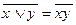
5. Операция отрицания: 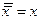
6. 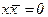
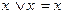
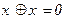
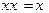
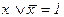
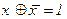
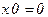
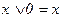
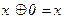

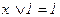
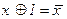
Опр2. a) Пусть H  P. Формулой будем называть любую функцию из множества
P. Формулой будем называть любую функцию из множества  .
.
Например, любая элементарная функция - формула.
b) Рассмотрим набор функций 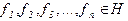 и рассмотрим функцию
и рассмотрим функцию
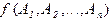 - формула
- формула 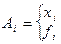
Формула представляет собой некоторую булеву функцию от совокупного множества переменных.
Опр3. Формула называется тождественно истинной (тождественно ложной), если реализуемая ею функция равна 1 (соответственно 0).
Опр4. Пусть заданна функция 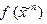 - функция от n переменных. Переменная
- функция от n переменных. Переменная 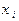 называется существенной, если существует такой набор
называется существенной, если существует такой набор  (из 0 и 1) значений переменных
(из 0 и 1) значений переменных 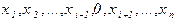 , для которого
, для которого 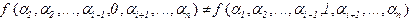 . В противном случае переменная называется фиктивной.
. В противном случае переменная называется фиктивной.
Функция задается тремя способами:
1) табличный, например таблица 1;
2) с помощью формул, например: 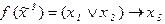
3) векторно, например: 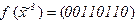
1.1.Выяснить, какие из перечисленных выражений являются формулами:
1) 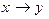
Решение: 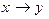 - формула, т.к. это элементарная функция.
- формула, т.к. это элементарная функция.
2) 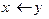
Решение: 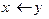 - не формула, т.к.
- не формула, т.к. 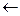 - не функциональный символ.
- не функциональный символ.
3)  4)
4) 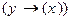 5)
5)  6)
6) 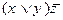
1.2.Построить истинностные таблицы для функций, реализуемых следующими
формулами:
1) 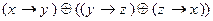
Решение: пользуюсь определениями элементарных функций, строим истинностную таблицу.

|
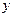
|

| 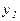
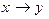
| 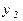
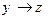
| 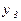

| 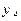
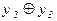
|

|
2) 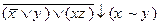 3)
3) 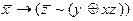 4)
4) 
1.3. Какие из перечисленных формул являются тождественно истинными или тождест-
венно ложными:
1) 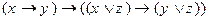
Решение: строим истинностную таблицу для заданной функции.

|
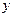
|

| 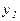
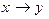
| 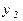
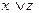
| 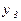

| 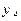

|

|
Ответ: данная формула тождественно истинная.
2) 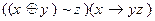 3)
3) 
4) 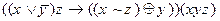 5)
5) 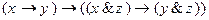
6) 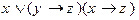
1.4. Перечислить существенные и фиктивные переменные следующих функций:
1) 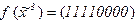

| 
| 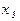
| 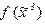
|
Проверим переменную  :
: 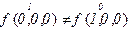
 - существенная переменная.
- существенная переменная.
Проверим переменную  :
: 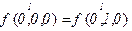
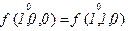
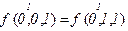

 - фиктивная переменная
- фиктивная переменная
Проверим переменную 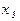 :
: 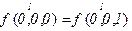
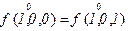
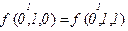
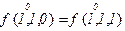
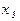 - фиктивная переменная
- фиктивная переменная
2) 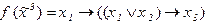 3)
3) 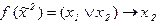
4) 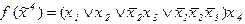 5)
5) 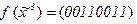
6) 
1.5. Показать, что  является фиктивной переменной функции
является фиктивной переменной функции  (выразив
(выразив  формулой, в которую
формулой, в которую  не входит явно):
не входит явно):
1) 
Решение: строим истинностную таблицу

| 
| 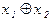
| 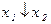
| 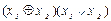
|

 - фиктивная перем.
- фиктивная перем. 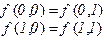
 - фиктивная перем.
- фиктивная перем.
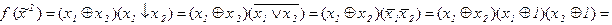
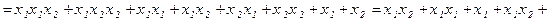
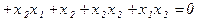
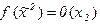
2) 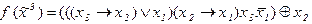
3) 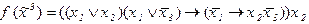
1.6. От каких переменных функция  зависит существенно.
зависит существенно.
1)  2)
2) 
3) 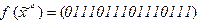 4)
4) 
1.7. Выяснить для каких 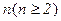 зависят существенно от всех своих переменных следующие функции:
зависят существенно от всех своих переменных следующие функции:
1) 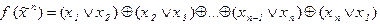
2) 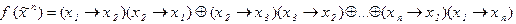
3) 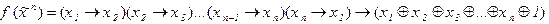
1.8. Эквивалентны ли формулы 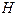 и
и 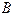 :
:
1) 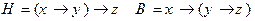
Решение: строим истинностную таблицу для функций 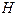 и
и 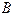

| 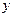
| 
| 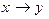
| 
| 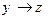
| 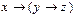
|
Ответ: 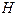 и
и 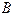 - не эквивалентны.
- не эквивалентны.
2) 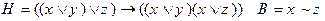
3) 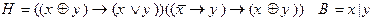
4) 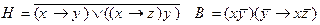
1.9. Проверить, справедливы ли следующие соотношения. Указание: справедливость данных соотношений проверяется составлением истинностных таблиц.
1) 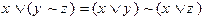 2)
2) 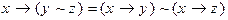
3)  4)
4) 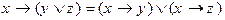
5) 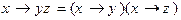 6)
6) 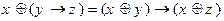
7) 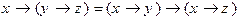
1.10. Используя основные эквивалентности, доказать эквивалентность формул 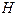 и
и 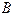 , если:
, если:
1) 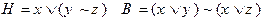
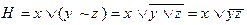

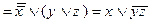
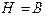
2) 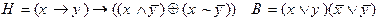
3) 
1.11. Реализовать функцию  формулой над множеством связок
формулой над множеством связок 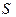 , если:
, если:
1) 
Решение: функцию 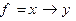 надо выразить через суперпозицию функций отрицание и дизъюнкцию:
надо выразить через суперпозицию функций отрицание и дизъюнкцию: 
2)  3)
3) 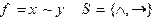 4)
4) 
Обозначим: 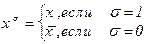
Если 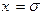 , то
, то  , если
, если  , то
, то 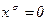 .
.
Опр 1. Формула вида 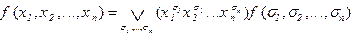 называется совершенной дизъюнктивной нормальной формой (с.д.н.ф.)
называется совершенной дизъюнктивной нормальной формой (с.д.н.ф.)
Опр 2. Формула вида 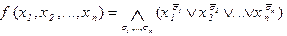 называется совершенной конъюнктивной нормальной формой.
называется совершенной конъюнктивной нормальной формой.
Опр 3. Формула вида 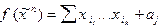 , где
, где 
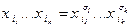 называется полиномом Жегалкина.
называется полиномом Жегалкина.
Опр 4. Пусть  . Тогда
. Тогда 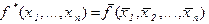 называется двойственной к функции
называется двойственной к функции 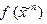 .
.
2.1. Построить СДНФ и СКНФ для следующих функций:
1) 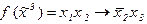
Решение: строим истинностную таблицу для данной функции:

| 
| 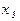
| 
| 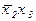
| 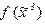
|
Строим СДНФ:
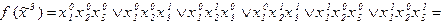

Строим СКНФ:

2) 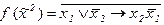
3) 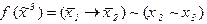
4) 
2.2. Используя основные логические законы, привести к с.д.н.ф. и с.к.н.ф.
1) 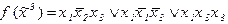
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 830; Нарушение авторских прав?; Мы поможем в написании вашей работы!