Применение средних величин при анализе показателей внешней торговли

При анализе показателей внешней торговли наряду с применением абсолютных и относительных величин широкое распространение получили средние величины (подраздел 1.4 настоящего пособия).

В таможенной статистике внешней торговли принято исчислять средние величины, характеризующие [19]:

- уровень цен на товары, обращающиеся во внешнеторговом обороте;

- уровень стоимостного и количественного объема экспорта и импорта товаров в общем и в разрезе товарных групп, товарных позиций, отдельных товаров и стран;

- средние темпы роста товарооборота, экспорта, импорта.

Для исчисления средних величин используются как абсолютные, так и относительные показатели внешней торговли. Наибольшее распространение при анализе показателей внешней торговли получили следующие виды средних величин:

- средняя арифметическая (простая и взвешенная);

- средняя гармоническая;

- средняя геометрическая (простая и взвешенная);

- средняя структурная – мода и медиана.

Средняя арифметическая простая рассчитывается по формуле (1.76).

Пример. Экспорт субъекта РФ в млн долларов за январь 2010 года составил 10,1, за февраль 20,7, за март – 18,9, за апрель – 21,6, за май – 27,3, за июнь – 15,8. Определить среднее значение экспорта субъекта РФ за первое полугодие 2010 года

млн долларов.

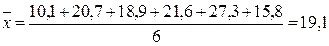
Ответ. Среднее значение экспорта субъекта РФ за первое полугодие 2010 года составляет 19,1 млн долларов.

Средняя арифметическая простая исчисляется в том случае, если варьирующие показатели встречаются в совокупности по одному разу и имеют одинаковый вес в совокупности.

Средняя арифметическая взвешенная исчисляется в случаях, когда варьирующие показатели встречаются в совокупности различное число раз и имеют различную значимость. Средняя арифметическая взвешенная рассчитывается по формуле (1.14).

Пример. Рассчитать среднюю цену за 1 тонну экспортируемой из РФ рыбы (таблица 2.4).

Так как цена товара зачастую зависит от его количества, то для определения средней цены за 1 тонну рыбы в текущем периоде применим формулу средней арифметической взвешенной:

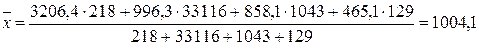долларов за тонну.

Таблица 2.4 – Экспорт рыбы свежей или охлажденной (код 0302).

Наименование товара	Базисный период	Текущий период
Количество, тонн	Стоимость, тыс долларов	Цена за тонну, долларов	Количество, тонн	Стоимость, тыс долларов	Цена за тонну, долларов
Камбала Треска Пикша Сайра			1225,9 1348,8 1003,3 479,8			3206,4 996,3 858,1 465,1

Ответ. Средняя цена за экспортируемую рыбу в текущем периоде составила 1004,1 долларов за тонну.

Средняя гармоническая используется, когда совокупность состоит из абсолютных и относительных показателей (удельный вес, темп роста и т.д.).

Средняя гармоническая исчисляется из обратных значений варьирующего показателя по формуле (1.16).

Пример. По данным об экспорте из РФ стриженной немытой шерсти в страны дальнего зарубежья в 2010 г. и темпам роста по каждой стране необходимо охарактеризовать динамику экспорта стриженной немытой шерсти в страны дальнего зарубежья за период 2009-2010 гг.

в тоннах

Страна назначения	2010 г., тонны	2010 г. в % к 2009 г. (темп роста)
Бельгия		110,4
Болгария		241,0
Великобритания		72,9
Венгрия		27,4
Германия		89,7

Темп роста в целом по данным странам дальнего зарубежья составит:

.

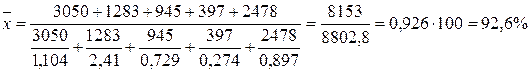Ответ. Экспорт из РФ в страны дальнего зарубежья стриженной немытой шерсти в 2010 г. по сравнению с 2009 г. сократился на 7,3%.

Средняя геометрическая простая, рассчитываемая по формуле (1.17) используется для исчисления величин, характеризующих средние темпы роста цен, товарооборота, экспорта, импорта как в целом, так и по отдельным товарам и странам.

Пример. Рассчитать средний темп роста экспортных поставок субъекта РФ за 2007-2010 гг.

Год
Темп роста, в коэффициентах	-	1,045	1,406	1,257

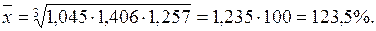
Ответ. Средний темп роста экспортных поставок субъекта РФ за период 2007-2010 гг. составил 123,5%.

Средний темп роста может быть рассчитан по формуле (1.85).

Пример. Рассчитать средний темп роста экспортных поставок субъекта РФ за 2007-2010 гг.

Год
Стоимость, млн долларов	42376,3	44297,4	62285,4	78290,2

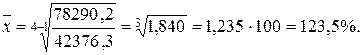
Средняя геометрическая взвешенная, рассчитываемая по формуле (1.18), используется в случае, если коэффициенты роста/падения относятся к периодам неодинаковым по продолжительности.

Пример. Коэффициент роста экспорта субъекта РФ за разные периоды:

2000-2004 гг.	2005-2008 гг.	2009-2010 гг.
1,152	1,047	1,011

Для расчета среднего темпа роста экспорта за период 2000-2010 гг. учитывается, что весь период составляет 11 лет и состоит из отрезков времени 5, 4 и 2, следовательно:

.

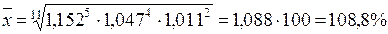Ответ. Средний темп роста экспорта субъекта РФ за период 2000-2010 гг. составил 108,8%.

Медиана – это величина признака, находящегося в середине ранжированного ряда.

Пример. Цена за 1 тонну ферросилиция, экспортированного из субъекта РФ в пять стран, составила ряд следующих величин

в долларах

Япония	Китай	Венгрия	Германия	Турция
314,8	339,9	362,2	397,0	443,2

Медианой этого ряда будет цена 362,2 долларов за тонну, т.е. в половину стран ферросилиций продавался по цене меньше, чем 362,2 долларов за тонну, а в остальные страны – по цене, большей названной.

Если ряд состоит из четного числа вариант, то медиана составит половину суммы двух показателей ранжированного ряда, находящихся в середине ряда.

Пример. Для приведенного ниже ранжированного ряда медиана рассчитывается так:

Ме = 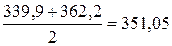долларов

в млн долларов

Япония	Китай	Венгрия	Германия
314,9	339,9	362,2	397,0

Мода – это величина признака, наиболее часто встречающегося в изучаемой совокупности. Мода исчисляется с целью выявить величину признака, который имеет наибольшее распространение.

Пример. По данным о цене за 1 тонну метанола в страны дальнего зарубежья необходимо определить моду цен, по которым заключено наибольшее количество контрактов.

Цена за 1 тонну метанола, долларов	Количество заключенных контрактов
167,6
194,6
238,0
254,1
329,7

Ответ. Модальной ценой контракта за рассматриваемый период является величина моды цен, равная 238 долларам, т.к. по этой цене было заключено наибольшее количество контрактов – 19.

Дата добавления: 2014-12-23