ВОПРОСЫ. Параметр ξ характеризует относительную “расстройку” между собс­твенной частотой системы (определяемой временем жизни каждой единичной

0 ≤ ε ≤ 1.

Параметр ξ характеризует относительную “расстройку” между собс­твенной частотой системы (определяемой временем "жизни" каждой единичной пластически деформированной стружки от момента её за рождения до момента её удаления с обрабатываемой поверхности, то есть определяемой частотой "стружкообразования" и частотой внешней импульсной нагрузки, вызванной воздействием на микро­масштабном уровне режущих зерен производящей инструментальной поверхности на обрабатываемую поверхность кристалла. Периоди­ческая импульсная нагрузка выражена через вторую обобщенную производную функции τ(ξ), определенной на периоде следующим об­разом:

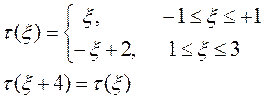
В уравнении (3.1) введено обозначение для четверти периода внешнего воздействия а = π/2, так что частота основного тока внешнего импульсного воздействия предполагается равной единице.

Параметр р обозначает безразмерную амплитуду внешнего им­пульсного воздействия в каждой точке касания каждого режущего зерна с обрабатываемой поверхностью.

Параметр τ является безразмерной осциллирующей переменной, выступающей в роди "быстрого" времени.

В роди "медленного" времени выступает безразмерный пара­метр t° = ε*τ.

Безразмерный параметр ε обобщенно характеризует параметры упругой обрабатывающей системы, определяющих статическую сос­тавляющую упругих деформаций этой системы.

Так как выбранные условия нагружения соответствуют тому, что z < 1. то величина ε *(z² - 1) отрицательна, что соответс­твует отрицательному затуханию в системе, описываемой уравнени­ем (3.1). Амплитуда z при этом со временем возрастает. Таким образом, заданное системе малое начальное перемещение или скорость вызывают возрастание амплитуды колебаний до тех пор, пока не установится периодическое движение о постоянной амплитудой ρ. Наоборот из этого уравнения также следует, что если задано большое начальное перемещение (z > 1) или скорость, то амплиту­да колебаний будет уменьшаться до тех пор, пока не установится такое же периодическое движение с постоянной безразмерной амп­литудой ρ.

Необходимость решения уравнения (3.1) обусловлена опреде­лением взаимосвязей между всеми безразмерными параметрами упру­гой обрабатывающей системы и, в том числе, выбором регулируемо­го параметра g в каждой точке касания каждого режущего зерна обрабатываемой поверхностью, при которых указанная безразмерная величина амплитуды ρ не превышала величины, соответствующей за­данной величину микронеровностей R_Z на окончательно обработан­ной поверхности.

Как правило для решения задач по механическим колебаниям широко применяют электронные моделирующие устройства. Для реше­ния уравнений Ван-дер-Поля (при условии равенства нулю правой части уравнения (3.1)) построена вычислительная цепь в таком электронном моделирующем устройстве с помощью которой проанали­зирован фазовый "портрет" этого уравнения s фазовой плоскости. в которой перемещение z и скорость откладывают по осям декартовой системы координат. Этот фазовый "портрет" показан на рис. 3.5.

Однако поведение исследуемой системы под воздействием пе­риодической импульсной нагрузки с применением электронных моде­лирующих устройств осуществить не представляется возможным. В связи с этим в данной работе предложен и разработан новый ана­литический метод исследования автоколебательных нелинейных систем, основанный на специальном преобразовании, содержащим пару, негладких функций (пилообразный Sin и прямоугольный Cos). Осо­бенности поведения системы рассмотрены в условиях внешней пери­одической импульсной нагрузки.

Действие мгновенных импульсов на механическую систему обычно описывается одним из двух способов.

Первый - подчинение переменных дополнительным условиям в окрестностях точек локализации импульсов. Это приводит к необ­ходимости рассматривать вместо одной системы целой серии систем (в промежутках между импульсами).

Другой путь состоит во введении в уравнения сингулярных функций, описывающих импульсы, и рассмотрении уравнений как ин­тегральных тождеств в рамках теории распределений. А это требу­ет дополнительных обоснований в нелинейном случае. В дан­ной работе описан метод негладкого преобразования аргумента, представляющий собой синтез упомянутых выше двух подходов. Ме­тод позволяет, с одной стороны, исключить сингулярные члены в уравнениях, а с другой, путем анализа краевой задачи на стан­дартном отрезке, подучить решения в виде единого аналитического выражения,на всем пространственном интервале.

Рис.3.5.

Фазовые траектории для уравнения Ван-дер-Поля при различных значениях параметра ε:

а) ε =0; б) ε =0,2; в) ε =0,5; г) ε =1;

1- траектория "предельного цикла".

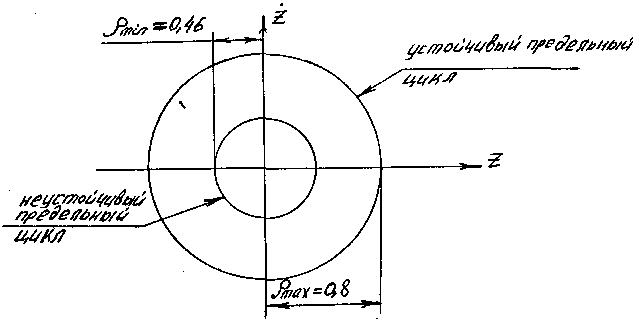
Рис. 3.6.

Резонансные кривые, полученные в результате решения уравнения (3.1).

Решение уравнения (3.1) будем искать в виде двухпараметри­ческого семейства. Воспользуемся идеей двухмасштабных разложе­ний.

Периодическое решение уравнения (3.1) разыскиваем в виде:

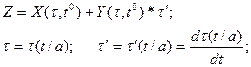(3.2)

где X(τ, t°), Y(τ, t°) - функции, подлежащие определению. Подставим (3.2) в уравнение движения (3.1). Приравнивая отдельно нулю члены, содержащие множитель τ и не содержащие его, также исключая появившиеся в результате дифференцирования сингулярные члены, получим систему уравнений (3.3) в частных производных:

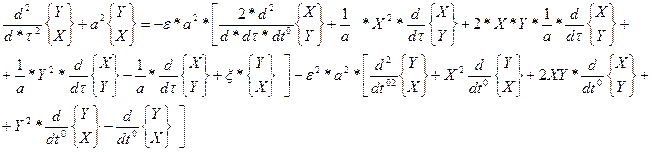
с краевыми условиями:

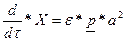(3.4)

За счет краевых условий исключен сингулярный член в урав­нении (3.1). Воздействие импульсной нагрузки на систему прояв­ляется в уравнении (3.4) с параметром р.

Решение задачи (3.3)-(3.4) разыскиваем в виде ряда по сте­пеням ε. Порождающей является несвязная (относительно X, Y-компонент) линейная однородная задача, особенность решения которой состоит в том, что она содержит неопределенные функции "медлен­ного" времени Ao(t°), Do(t°). Функции Ao(t°) и Do(t°) определя­ются на следующем шаге асимптотической процедуры. В первом приближении имеем нелинейную задачу. Она содержит резонансные слагаемые, что приводит к появлению секулярных членов в реше­нии. Однако поскольку новый параметр τ ограничен (-1 ≤ τ ≤ 1) и является периодической функцией исходного времени t, эти "секулярные" члены сохраняем. Произвольным выбором функций "медлен­ного" времени среди оставшихся членов в решении распоряжаемся для удовлетворения краевым условиям. Тогда, уравнения для опре­деления функций Ao(t°) и Do(t°) имеют вид:

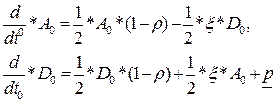, (3.5)

где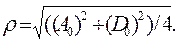

Усреднение уравнения для определения функций "медленного" времени " нелинейны. Однако принятое упрощение по сравнению с исходным уравнением состоит в том, что оно описывает только "медленную" составляющую и не содержит сингулярных членов.

Окончательный результат решения уравнения (3.1) после двух последовательных процедур асимптотических приближений (с первым и вторым порядком по ε) имеет вид:

Z = Ao-Sin(a-τ)+ε*X₁+(D_o*Cos(a*τ)+ε*Y₁)+0(ε²)

В первом асимптотическом приближении получены условия су­ществования периодического режима в системе (3.1).

Периодические процессы соответствуют положительным вещест­венным корням уравнения резонансной кривой

(l-ρ)³-ρ*ξ²= p ² (3.6).

Уравнение (3.6) дает зависимость между:

- безразмерной p - амплитудой внешнего импульсного воздействия в каждой точке касания каждого режущего зерна произво­дящей инструментальной поверхности с обрабатываемой поверх­ностью на частоте внешнего воздействия;

- безразмерным параметромρ, отражающим наибольшую ампли­туду периодических колебаний упругой обрабатывающей системы в момент динамического равновесия между фактическим нагруженном ритмичным полем обрабатываемой поверхности и фактической реак­цией этой поверхности в виде послойного дискретного (порционно­го) съема припуска с множеством единичных пластически деформи­рованных "стружек" в каждой дискретной порции;

- параметром ξ, характеризующим относительную "расстройку" между собственной частотой автоколебаний упругой обрабатывающей системы в установившемся режиме микрошлифования и частотой внешней импульсной нагрузки ритмичного поля на обрабатываемую поверхность.

Кроме того, для обеспечения периодических процессов необ­ходимо выполнить условия, при которых с одной стороны будет иметь место вещественный положительный корень в уравнении (3.6) относительно р, а, с другой стороны, если будут выполнены усло­вия:

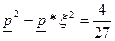
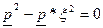
(один вещественный корень относительно ρ в уравнении (3.6));

(три вещественных корня относительно ρ в уравнении (3.6)

На границе между областями

(два вещественных положительных корня относительно ρ в уравнении (3.6), один из которых двухкратный).

При значении параметров р и ξ из области существования одного вещественного положительного корня ρ в уравнении(3.6).например, р =0,39 и ξ=0,105, то при р =0,39 устанавливается пре­дельный цикл (периодическое решение) (рис.3.6).

Выполненные численные расчеты по уравнению (3.1) показали совпадение аналитического и численного решения. В том случае. если параметры р и ξ, принадлежат области, где не существует ве­щественного положительного корня р уравнения (3.6), например. Р =0,8 и ξ=1.5, то предельный цикл не устанавливается.

Если нелинейность упругой обрабатывающей системы (3.1) не мала, то воздействие внешней периодической силы может привести к установлению очень сложных режимов колебаний. Такие колебания могут быть исследованы только численными методами.

Подученные аналитические зависимости описывают отдельно движение упругой обрабатывающей системы как в статике (для оп­ределения её размерной настройки), так и в динамике (для опре­деления величины шероховатости Rz на окончательно обработанной поверхности).

Для определения в каждой конкретной упругой обрабатывающей системе фактических (как статических, так и динамических) па­раметров её движения используют тестовые методы идентификации этих параметров, прежде всего идентифицируют фактическую вели­чину постоянной времени переходных процессов резания Т_п, интег­рально отражающего фактическое состояние её как динамических характеристик (амплитуду λ и частоту f_c динамической составляю­щей упругих деформаций), так и статических её характеристик (статическую составляющую Д упругих деформаций) в виде соотно­шения

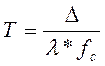(сек) (3.8)

Используют уравнение (3.8) для определения в каждой конк­ретной упругой обрабатывающей системе параметра fc, а затем оп­ределяют фактическую величину "расстройки" ξ, из соотношения:

(5.9) и (3.10)

где f - частота внешней импульсной нагрузки, с^-1;

m - количество радиальных, выступов на производящей инструментальной поверхности шлифовального круга;

n - количество оборотов шлифовального круга за одну минуту.

Затем из совместного решения уравнения (3.6). условий (3.7), уравнений (3.9) и (3.10) для каждой упругой обрабатываю­щей системы определяют фактические величины параметровρ_ф и p _ф. Полученные результаты сопоставляют с заданными выходными пара­метрами (по высоте микронеровностей R_z) на окончательно обрабо­танной поверхности и, при необходимости, корректируют параметр р _ф для приведения ρ_ф к заданному значению R_z. Пример одного из таких сопоставлений при одновременном функционировании двух уп­ругих обрабатывающих систем (при обработке натуральных алмазов в различных (одной - при обработке в "мягком", а другой - при обработке в "твердом") направлениях представлена в таблице 3.1.

Анализ этой таблицы позволяет сделать следующие выводы:

1. При обработке в "твердом" и в “мягком" направлениях возможна одновременная обработка одним и тем же шлифовальным кругом, гладкая производящая инструментальная поверхность кото­рого не имеет радиальных выступов. В этом случае при составле­нии управляющей программы, взаимоувязывающей координатные пере­мещения по осям X, Y, Z в функции угла поворота производящей инструментальной поверхности отсутствующие реальные радиальные выступы заменяют "виртуальными", а микроподачу в каждой точке касания каждого режущего зерна с обрабатываемой поверхностью на всей длине продольного перемещения (между точками реверса) осу­ществляют только от цифрового пьезоэлектрического привода. При­чем величина каждого такого дискретного перемещения на глубину резания соответственно для изделий "мягкого" и "твердого" нап­равлений составляет 0,00027 мкм и 0,0007 мкм соответственно (при этом R_Z = 0,05 мкм).

2. При обработке и в "твердом" и в "мягком" направлениях возможна одновременная обработка одним и тем же шлифовальным кругом, имеющем на производящей инструментальной поверхности 30000 реальных радиальных выступов с высотой каждого из них. равной 0,022 мкм. В этом случае через каждые 101156 импульсных воздействий указанными радиальными выступами на изделие с "мяг­ким" направлением и, соответственно, через каждые 157867 им­пульсных воздействий той же производящей инструментальной по­верхности на изделие с "твердым" направлением осуществляют от цифрового пьезоэлектрического привода дискретная врезная подача на глубину резания составляет 0,03 мкм (при этом Rz = 0,03 мкм).

Таблица 3.1. Параметры упругой системы при обработке алмазов.

	“Мягкое” направление fвнеш=1500000 с^-1
Nm	Тм, С	qм	σм, мкм	Δм, мкм	Wм |		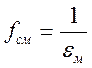ρм	р м	Rzv, мкм	γм, мкм
(1-ρ)^3- ρ*ξ^2= p ^2 и р ^2- р *ξ^2=0 Устойчивый предельный цикл		1.7(3)	0,9(09)		1,285		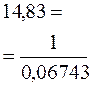	0,8432	0.00455	0,05	0.00027
(1- ρ)^3- ρ*ξ^2= р ^2 р ^2- р *ξ^2=4/27 Неустойчивый предельный цикл		1,7(3)	0.9(09)		1,285		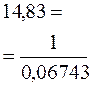	0.4668	0.38718	0,03	0.022

Таблица 3.1. (продолжение)

	“Твердое направление fвнеш=15000000 с^-1   "Т з е £ э д о е" н а п р а в j s e н и е j 'внеш ^s^= с-^1
nt	Тт, С	qт	δт, мкм	Δт, мкм	Wt		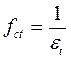ρт	PT	rzt, мкм	γт, мкм
(l-ρ)^3-ρ*ξ^2= р^2 и р ^2- р *ξ^2=0   Устойчивый предельный цикл		22.7(6)	0,99(24)	0.669	10.788			0.7928	0.01108	0.05	0.0007
(l-ρ)^3-ρ*ξ^2= р ^2 и р ^2- р *ξ^2= 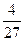  Неустойчивый предельный цикл		22,7(6)	0,99(24)	0,669	10.788			0,46	0.39	0.03	0.022

1. Что изучает физическая мезомеханика материалов?

2. Что включает в себя упругая обрабатывающая система шлифовального станка?

3. Какие существуют масштабные уровни потери сдвиговой устойчивости в деформируемом твердом теле в процессе шлифования?

4. Как в процессе шлифования происходит потеря сдвиговой устойчивости на микроуровне?

5. Как в процессе шлифования происходит потеря сдвиговой устойчивости на мезоуровне?

6. Что такое фрагментация материала в процессе пластичного микрошлифования?

7. Какие процессы происходят в нагруженном твердом теле на макроуровне?

8. Назовите физические условия зарождения и распространения трещин при разрушении?

9. Влияние нормальной и тангенсальной составляющих силы резания на процесс размерно-регулируемого микрошлифования?

10. Объясните модель управления процессом микрорезания твердоструктурных и хрупких материалов в процессе шлифования?

ЗАКЛЮЧЕНИЕ

Изложенная теория пластической деформации в мезообъемах является основой для бездефектного размерно-регулируемого шлифования анизотропных твердоструктурных и хрупких материалов, в том числе и натуральных алмазов, кристаллографически ориентированных по плоскости (111) (т.е. в «твердом» направлении) с получением нанометрового рельефа на обработанной поверхности.

Современные требования полупроводниковой промышленности, микро- наноэлектроники, медицины и гранильной отрасли к стабильному качеству обработанных алмазов и алмазоподобных материалов диктует необходимость автоматизации процессов обработки, которые можно обеспечить только на основе применения диагностирования параметров этого процесса.

Методологические основы использования теории пластической деформации в мезообъемах для автоматизации огранки алмазов в бриллианты излагаются в соответствующем учебном пособии.

ЛИТЕРАТУРА

Дата добавления: 2014-12-27