Работа при изопроцессах

Молярная теплоемкость при постоянном давлении (Cp).

Уравнение Майера

Если газ нагревается при p = const, то

не зависит от вида процесса (внутренняя энергия идеального газа dU не зависит ни от р, ни от V, а определяется только Т) и всегда равна C_v.

Дифференцируя уравнение Клапейрона-Менделеева pV_µ = RT по Τ при

p = const, получим

C_p=С_V +R — уравнение Майера

С_p всегда больше С_V на величину универсальной газовой постоянной.

Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

При рассмотрении термодинамических процессов важную роль играет величина

которая называется коэффициентом Пуассона.

Изопроцессы – это равновесные процессы, происходящие с термодинамическими системами, при которых один из основных параметров состояния сохраняется постоянным.

7.1. Изохорный процесс (V = const)

Диаграмма этого процесса — изохора — в коор­динатах (p,V) изображается прямой, параллельной оси ординат (ось p). Процесс 2-1 — изохорный нагрев, процесс 2-3 — изохорное охлаждение. При изохорном процессе газ не совершает работу над внешними телами (δΑ = pdV = 0) и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии (δQ = dU). Поскольку dUμ = Cv·dT, то для произвольной массы газа:

7.2. Изобарный процесс (р = const)

Диаграмма этого процесса — изобара — в координатах (p,V) изобра­жается прямой параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от Vl до V2 равна: и определяется площадью заштрихованного прямоугольника.

Используя уравнение Менделеева-Клайперона

, получаем ,

отсюда, или .

Физический смысл универсальной газовой постоянной R:

R численно равна работе изобарного расширения 1моля идеального газа при нагревании его на 1 К.

7.3. Изотермический процесс (Т = const)

Диаграмма этого процесса — изотерма — в коор­динатах (p,V) представляет собой гиперболу. Изотермический процесс описывается законом Бойля-Мариотта (pV = const). Работа изотермического расширения газа:

Так как при T = const внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что δQ = δA, то есть все количество теплоты, сообщаемое газу, расходуетсяна совершение имработы против внешних сил.

Поэтому, для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

8. Адиабатический процесс (δQ = 0).

Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0).

К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д.

Из первого начала термодинамики следует, что при адиабатическом процессе

Используя и , получим

(1)

C другой стороны, из следует (2)

Разделив (2) на (1) получим:

или , (3)

где - коэффициент Пуассона. Интегрирование уравнения (3) дает

Откуда следует уравнение Пуассона – уравнение адиабатического процесса:

используя уравнение Менделеева-Клайперона 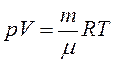, получаем:

Диаграмма адиабатического процесса – адиабата - в координатах (p,V) изображается гиперболой.

Адиабата (pV^γ = const) более крута, чем изотерма (pV = const). Это объясняется тем, что при адиабатическом сжатии (1 – 3) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры.

9. Работа газа в адиабатическом процессе

В адиабатическом процессе 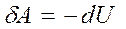, поэтому .

Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от Т₁ до Т₂ и работа расширения идеального газа:

,

Откуда получаем, используя уравнение Менделеева-Клапейрона :

.

Работа адиабатического расширения 1-2 (заштрихованная площадь) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

10. Политропические процессы (С = const)

Процесс, в котором теплоемкость остается постоянной (С = const) называется политропическим.

Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы — это частные случаи политропного процесса.

Уравнение политропы: pVⁿ = const

где коэффициент называется показателем политропы.

Значения теплоемкости и показателя политропы для разных процессов приведены в таблице:

Процесс	С	n
Адиабатический	С = 0	n = γ
Изотермический	С = ∞	n = 1
Изобарический	С = Ср	n = 0
Изохорный	С = СV	n = ± ∞

Теплоемкость при изотермическом процессе бесконечно велика, поскольку температура не изменяется (dT = 0) при подводе тепла (δQ ≠ 0).

Теплоемкость при адиабатическом процессе равна нулю, поскольку нет подвода тепла (δQ = 0), хотя температура изменяется (dT ≠ 0).

11. Круговой процесс (цикл)

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние.

На (p,V)- диаграмме цикл изобража­ется замкнутой кривой, где участок 1-2 соответствует расширению, а 2-1 — сжатию газа.

Работа расширения А₁ (площадь фигуры 1a2V₂V_l1) положительна: А₁ > 0.

Работа сжатия А₂ (площадь фигуры 2b1V₁V₂2) отрицательна: А₂ < 0.

Работа за цикл А определяется площадью, охватываемой замкнутой кривой:

А = А₁ + А₂

Таким образом, работа — это функция не только состояния термодинамической системы, но и вида процесса, который происходит. Поэтому работа не является однозначной функцией состояния (такой, как внутренняя энергия).

Из первого начала термодинамики следует, что теплота Q, так же как и работа А, является функцией процесса, который происходит с системой.

Цикл называется прямым, если за цикл совершается положительная работа

(цикл протекает по часовой стрелке — рисунок (А)).

Цикл называется обратным, если за цикл совершается отрицательная работа

(цикл протекает против час. стрелки — рисунок (Б)).

Прямой цикл используется в тепловых двигателях (совершают работу за счет полученной извне теплоты).

Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).

12. КПД кругового процесса.

В результате кругового процесса система возвращается в исходное состояние, следовательно, полное изменение внутренней энергии равно нулю.

Поэтому Q = ΔU + А = А,

т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты.

Если в ходе кругового процесса система не только получает количество теплоты Q₁, но и теряет (отдает) количество теплоты Q₂, то

Q = Q₁ - Q₂

Термический коэффициент полезного действия для кругового процесса — это величина, равная отношению работы, совершенной системой, к количеству теплоты, полученному в этом цикле системой:

13. Обратимый и необратимый процессы

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлениях.

Причем, если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений.

Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Реальные процессы необратимы, в них всегда происходит диссипация (потеря) энергии (из-за трения, теплопроводности и т.д.).

Дата добавления: 2014-12-27