
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Композиция оценок свойств и сравнение альтернатив
|
|
|
|
Переход от сравнения отдельных свойств к сравнению альтернатив является задачей композиции. Возможны различные случаи решения этой задачи.
а) Случай, когда все свойства оценены численно — получен набор критериев.
Пусть Ck(ci) — численная оценка k -го свойства i -ой альтернативы,
k =  .
.
Введем векторное пространство, называемое критериальным, в котором каждой i -ой альтернативе будет соответствовать точка: C(ci) = { C1(ci), C2(ci),..., Cm(ci) }, т.е. k -ой составляющей вектора C(ci) является Ck(ci) - численная оценка k -го свойства i -ой альтернативы.
При сравнении двух альтернатив c1 и c2 альтернатива c1 будет предпочтительнее альтернативе c2, если Ck(c1) ³ Ck(c2), для всех k=  причем хотя бы одно неравенство строгое. Здесь и далее рассматривается случай, когда лучшему свойству соответствует большее значение численной оценки. В противном случае перед численными оценками свойств можно ставить знак «минус».
причем хотя бы одно неравенство строгое. Здесь и далее рассматривается случай, когда лучшему свойству соответствует большее значение численной оценки. В противном случае перед численными оценками свойств можно ставить знак «минус».
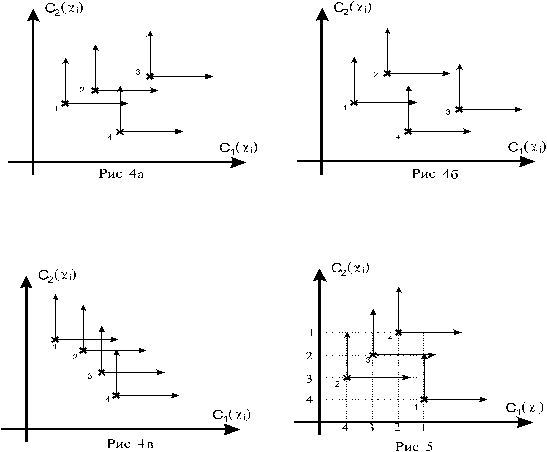
Поясним, как можно найти предпочтительные альтернативы, используя критериальное пространство. Рассмотрим для этого пример, когда альтернативы оцениваются по двум критериям. Принимая точку, соответствующую i -ой альтернативе, за начало координат, перенесем в эту точку все координатные оси критериального пространства. Если в положительном октанте полученной таким образом системе координат не окажется ни одной точки, соответствующей какой то другой альтернативе, то i -ая альтернатива является не улучшаемой.
На рис. 4а только одна неулучшаемая альтернатива — это альтернатива 3, на рис. 4б таких альтернатив две — 2 и 3, а на рис. 4в все альтернативы неулучшаемые.
Множество неулучшаемых альтернатив — это множество Парето. Получение множества Парето — 1-й шаг поиска лучшего решения. Есть много других, кроме рассмотренного, эффективных методов изучения множеств Парето.
Для выбора альтернативы на множестве Парето нужно привлекать другие соображения, связанные с особенностями решаемой задачи.
б) Случай, когда нет численных оценок, а есть только результаты попарного сравнения.
Пусть каждая альтернатива характеризуется n -свойствами и по каждому из этих свойств проведена операция пожарного сравнения. Все операции обладают свойствами транзитивности и антирефлексивности. Если сравнение возможно для каждой пары альтернатив по каждому свойству, то оказывается возможным все альтернативы ранжировать по каждому свойству, при этом будет получен набор перестановок из альтернатив — матрица с n -столбцами (по числу свойств) и m -строками (по числу альтернатив).
Пример. Пусть имеют место четыре альтернативы, каждая из которых характеризуется двумя свойствами. Результаты попарного сравнения имеют вид:
- по свойству 1: c1R1c4, c4R1c3, c3R1c2
- по свойству 2: c4R2c3, c3R2c2, c2R2c1
Соответственно матрица результатов сравнения имеет вид:
| Альтернативы | свойство 1 | свойство 2 |
| I | ||
| II | ||
| III | ||
| IV |
Один из способов дальнейшей работы с матрицей попарного сравнения — ввод условного векторного пространства свойств. Альтернативы располагаются на каждой из i -ых осей искусственно введенного критериального пространства в соответствии с их ранжированием по i -му свойству. Затем выделяются неулучшаемые альтернативы таким же способом, как в предыдущем случае.
Для приведенного выше примера 2-х альтернатив с 4-мя свойствами условное пространство свойств имеет вид, показанный на рис. 5.
В рассмотренном примере неулучшаемыми альтернативами являются 1 и 4.
После получения множества неулучшаемых альтернатив дальнейший выбор производится, как и в предыдущем случае, с учетом физической сущности процесса по какому либо правилу свертки множества критериев.
В рассмотренном примере в качестве лучшей может быть признана, например, альтернатива 4, у которой сумма рангов свойств наименьшая,
(2+1) < (1+4).
Более сложным является случай неполноты ранжирования.
5.3 Пример модели принятия решения
в условиях неопределенности
В условиях неопределенности принцип выбора зависит, как отмечалось выше, от характера противодействия противной стороны (внешней среды). В тех случаях, когда среда «ведет себя» антагонистическим образом по отношению к решению, выбранному органом управления системы, имеет место ситуация, относящаяся к теории игр. Если среда «пассивна» (например, это пассивная природа) и управляющему органу известно распределение вероятностей на множестве состояний среды, то имеет место «игра с природой» или «статистические решения». В общем случае возможна целая градация ситуаций, определяющих стратегию поведения среды.
Рассмотрим далее информационную ситуацию, когда распределения вероятностей на элементах состояния среды: априори известны. Рассмотрим простейший случай, не будем привлекать такие понятия как функция правдоподобия, функция потерь.
Итак, распределение вероятностей задано в виде ряда:
P= (p1,..,pj,.., pl ), pj= P(q=qj),  =1, где
=1, где  qj —состояние среды.
qj —состояние среды.
Это одна из возможных простейших ситуаций. На практике расчет априорного распределения вероятностей состояния среды производится либо путем обработки статистического материала, либо аналитическими методами на основании гипотез о поведении среды.
Обозначим.
1) c = { c1,.., ci,..,cm } — множество возможных альтернатив — вариантов принятия решения;
2) q ={ q1,.., qj,.., ql } — множество возможных состояний среды, причем вероятности этих состояний известны: Pj = P { q = qj };
3) Ф = {j1,.., jt,.., jr} — множество принципов (методов) выбора и оценки принятого решения;
С методом выбора решения связано понятие оценочного функционала — F.
F = {fi,j}, где fi,j — выигрыш (потеря), если при состоянии среды
qj Î q было принято решение ciÎc.
Будем считать, что оценочный функционал имеет положительный ингредиент и обозначается F+, если ставится задача достижения максимума: max{fi,j}. При отрицательном ингредиенте функционала F- лучшему решению соответствует min {fi,j}.
Таким образом ситуация принятия решения характеризуется тройкой {q,c,F}.
Соответственно, может быть получена матрица значений оценочного функционала (ситуационная матрица)

Различным принципам выбора соответствуют определенные критерии выбора – алгоритмы, которые определяют единственное оптимальное решение или множество таких решений. Для рассматриваемой ситуации могут быть использованы критерий Байеса, критерий минимакса (максимина), критерий минимума дисперсии оценочного функционала и др.
Рассмотрим эти подходы на примере.
Пусть оценочный функционал имеет положительный ингредиент, и ситуационная матрица имеет вид:
| q | q1 | q2 | q3 |
| R{q=qj} | 0.2 | 0.3 | 0.5 |
| c1 | |||
| c2 | |||
| c3 |
При использовании критерия Байесса максимизируется (в задаче на максимум) математическое ожидание результата. (Рассмотрен простой пример без использования решающих функций).
B*(P,ci)  =
= 

В рассматриваемом примере: В случае принятия альтернативы:
c1 — B*(P,c1) = 5·0,2 + 4·0,3 + 3·0,5 = 3,7.
c2 — B*(P,c2) = 4·0,2 + 5·0,3 + 5·0,5 = 4,2
c3 — B*(P,c3) = 4·0,2 + 2·0,3 + 4·0,5 = 3,4
Таким образом, согласно этому принципу наиболее предпочтительной является альтернатива c2.
При максминном подходе (в задаче на максимум) максимизируется наихудший из возможных результатов. (Здесь рассматриваются только чистые стратегии).
В*= 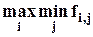
В рассматриваемом примере: в случае c1: min(5,4,3) = 3;
в случае c2: min(1,5,5) = 1;
в случае c3: min(4,2,4) = 2;
И согласно этому принципу наилучшей является альтернатива c1, которой соответствует максимум минимального результата.
Аналогично может быть решена задача на минимум.
В случае смешанных стратегий находится В*(ci,pi), отличающееся отнайденного выше В*.
5.4. Примеры решения оптимизационной задачи
методом динамического программирования
Динамическое программирование — метод оптимизации задач (процессов, операций), решение которых может быть разбито на несколько этапов, а целевая функция является, соответственно, аддитивной (или мультипликативной).
Пусть задача (процесс) разбита на n этапов,  .
.
Целевая функция — суммарный выигрыш в задаче на максимум (суммарные потери в задаче на минимум) запишется в виде:



 , где
, где  — выигрыш (потери) на i-м этапе.
— выигрыш (потери) на i-м этапе.
На каждом i-м этапе система (процесс) может находиться в одном возможном для этого этапа состояний — ski,  , здесь Si — множество всех состояний системы (процесса) на i-м этапе. В каждом состоянии системы ski могут быть принято одно из возможных, согласно условиям задачи (операции), решений (управлений) — aj,ki, где
, здесь Si — множество всех состояний системы (процесса) на i-м этапе. В каждом состоянии системы ski могут быть принято одно из возможных, согласно условиям задачи (операции), решений (управлений) — aj,ki, где  , здесь Aki — множество всех допустимых решений (управлений) при нахождении системы (процесса) на i-м этапе в k-м состоянии.
, здесь Aki — множество всех допустимых решений (управлений) при нахождении системы (процесса) на i-м этапе в k-м состоянии.
В результате принятия решения система (процесс) переходит в sl,i+1 состояние, при этом имеет место выигрыш (потери), равные  .
.
Таким образом, в результате принятия j-го решения система (процесс) перемещается с этапа i на этап i+1, при этом в зависимости от принятого решения переходит из состояния sk в состояние s l, а целевая функция получает приращение 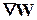 k, i(j).
k, i(j).
Существо метода заключается в том, что, начиная с последнего этапа, на каждом i-м этапе для каждого k-го состояния ищется так называемый условный оптимум W+k,i, являющийся суммой текущего приращения целевой функции и оптимального значения целевой функции от i+1 — го этапа до конца процесса
При этом. в результате управления, принятого на i-м этапе, система (процесс) перейдет на i+1-м этапе в состояние, зависящее от решения, принятого на i-м этапе.
Основное рекуррентное соотношение метода запишется в виде:
 , где
, где  — функция, определяющая в какое состояние перейдет система (процесс) из состояния k на этапе i при воздействие на систему управления aj,ki.
— функция, определяющая в какое состояние перейдет система (процесс) из состояния k на этапе i при воздействие на систему управления aj,ki.
После последовательного вычисления всех условных оптимумов от последнего n-го этапа до 1-го будет получен абсолютный оптимум и определен вектор управлений Aопт = (a1, a2,…,aj,ki,…,an), обеспечивающий этот оптимум.
Пример 1. Задача о размещении инвестиций
Пусть сумма в 5 млрд. может быть вложена (инвестирована) в четыре предприятия. Эта сумма может быть разделена произвольно с дискретностью в 1 млрд. Ожидаемая прибыль (дивиденды)  в зависимости от суммы вложения для каждого p-го предприятия показана в табл. 1.
в зависимости от суммы вложения для каждого p-го предприятия показана в табл. 1.
Табл.1

| 0 | 9 | 12 | 14 | 16 | |
 
| 0 | 4 | 10 | 13 | 14 | 15 |

| 0 | 3 | 7 | 11 | 15 | 17 |

| 0 | 6 | 11 | 12 | 13 | 14 |
 Из данных таблицы следует, что инвестиция в 1 млрд. в предприятие 1 даст прибыль в 5 млн., в пр. 2 — 4 млн., в пр. 3 — 3 млн., в пр. 4 — 6 млн. Аналогично интерпретируются данные остальных столбцов таблицы. Необходимо так распределить 5 млрд., чтобы получить максимум суммарной прибыли.
Из данных таблицы следует, что инвестиция в 1 млрд. в предприятие 1 даст прибыль в 5 млн., в пр. 2 — 4 млн., в пр. 3 — 3 млн., в пр. 4 — 6 млн. Аналогично интерпретируются данные остальных столбцов таблицы. Необходимо так распределить 5 млрд., чтобы получить максимум суммарной прибыли.
В этой задаче в терминах динамического программирования этапами является выделение определенной суммы очередному предприятию, состояние системы — размер суммы, которая делится между очередным предприятием и остальными, управление — решение о разделе суммы. Поскольку здесь номер предприятия условен на конечном этапе можно рассмотреть любое предприятие. Пусть это будет предприятие №1.
Для конечного 4-го этапа (нумерация этапов ведется от начала процесса) возможны шесть состояний: осталось для выделения 1-му предприятию 0, 1, 2, 3, 4, 5 млрд. Управление единственное для каждого состояния — оставшаяся сумма передается предприятию №1. Полученная прибыль приведена в табл. 2.
Табл.2
| 5 | ||||||||
| W4 | 0 | 5 | 9 | 12 | 14 | 16 | ||
На этапе 3 производится распределение средств между 1-м и 2-м предприятиями. Возможны те же шесть состояний, что и в предыдущем случае, однако для каждого состояния возможны шесть решений: 2-му предприятию выделяется 0, 1, 2, 3, 4, 5 млрд., соответственно. Результаты распределения показаны в табл.3.
Поясним, как заполняется табл.3. Состояние системы определено в верхней строчке таблицы, управление — в левом столбце. Пусть система находится в состоянии 3 (делится 3 млрд.) и принято решение о выделении предприятию 2 двух млрд. Тогда прибыль от 2-х млрд. составит 10 млн., оставшейся 1млрд. передается предприятию 1 и даст прибыль в 5 млн.
Суммарная прибыль при таком решении о распределении 3 млрд. составит 15 млн., что и показано в таблице. Для каждого состояния системы определяется решение, обеспечивающее максимум прибыли. Соответствующие цифры выделены в столбцах и перенесены на последнюю строчку.
Табл.3
| 0 | 9 | 12 | 14 | 16 | ||
| - | 4 | 9 | 13 | 16 | 18 | |
| - | - | |||||
| - | - | - | 13 | 18 | 21 | |
| - | - | - | - | 14 | 19 | |
| - | - | - | - | - | 15 | |

|
Таким образом, получен результат оптимального распределения средств между 1-м и 2-м предприятиями, т.е. получены условные оптимумы для 3-го этапа.
Информация относительно следующего 2-го этапа содержится в табл.4.
Табл.4
| - | 3 | 8 | 13 | 18 | ||
| - | - | 7 | 12 | 17 | ||
| - | - | - | 11 | 16 | 21 | |
| - | - | - | - | 15 | 20 | |
| - | - | - | - | - | 17 | |

|
На этом этапе происходит распределение вложений между 1, 2 и 3 предприятиями. Состояний системы по-прежнему шесть (верхняя строка таблицы). Управление для каждого состояния заключается в выделении 3-му предприятию от 0 до 5 млрд. (левый столбец таблицы). При выделении какой либо суммы 3-му предприятию результат оптимального распределения остатка между 1 и 2 предприятиями берется из последней строки таблицы 3. Например, в состоянии 4 (делятся 4 млрд.) принимается решение выделить 3-му предприятию 1 млрд., что обеспечит прибыль в 3 млн., распределение оставшихся 3-х млрд. даст прибыль в 15 млн. Суммарный результат в таблице — 18 млн. Максимизируя прибыль для каждого состояния системы (по столбцам), получим на последней строчке таблицы результат оптимального распределения выделяемой суммы между 1, 2 и 3 предприятиями (условные оптимумы для каждого состояния системы).
Последний (1-ый с начала нумерации) этап. Состояние системы одно — распределяется вся сумма. Управление заключается в том, какую часть этой суммы выделяется 4-му предприятию. Результат оптимального распределения остатка берется из последней строки таблицы 4. Информация относительно 1-го этапа содержится в табл.5
Как следует из анализа табл. 5, максимальная прибыль в 26 млн. будет получена при выделении 4-му предприятию 2 млрд. Чтобы выяснить, как при этом должна распределяться оставшаяся сумма в 3 млрд., возвратимся назад последовательно к таблицам 4, 3, 2.
Табл.5
| 22 | |
| 25 | |
| 22 | |
| 18 | |
| 14 | |
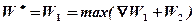
|
Из табл. 4 следует, что для состояния 3 оптимум будет получен, если 3-му предприятию ничего не выделяется, т.е. сохраняется состояние 3. Переходим к табл. 3.
Из табл. 3 следует, что при разделении 3 млрд. между 1 и 2 предприятиями необходимо для получения оптимальной прибыли 2-му выделить 2 млрд., 1-му — 1 млрд.
Таким образом, оптимальное управление обеспечивается вектором (1, 2, 0, 2), что соответствует прибыли в 26 млн. Действительно, если обратиться для проверки к таблице 1, получим, что выделение предприятиям 1, 2, 3, 4, соответственно 1, 2, 0, 2 млрд. даст суммарную прибыль 5+10+0+11=26 млн.
В предыдущем примере рассмотрен детерминированный вариант задачи, т.е. такой случай, когда все решения принимает человек. В стохастическом варианте задачи решения на определенных этапах носят случайный характер и их результаты могут быть осмыслены с помощью вероятностных оценок. Рассмотрим соответствующие примеры.
Пример 2. Задача о ремонте.
Пусть при работе на некотором станке в течение недели будет получен доход Q = 100 р., а при выходе на этом отрезке времени станка из строя доход Q = 0 р. Если будет предварительно проведена профилактика, то вероятность выхода станка из строя равна q = 0,4, в противном случае, без профилактики эта вероятность равна q = 0,7. Стоимость профилактики 20 р. Целесообразно или не целесообразно проводить профилактику?

Рис. 6
Для решения этой задач методом динамического программирования построим дерево решения (рис. 6). На рисунке кружками показаны узлы (состояния системы), где решение принимает человек, квадратами — узлы, где решение носит вероятностный характер.
Анализ начинается с последнего этапа. На последнем этапе возможны 4-ре состояния. Соответствующий выигрыш W3 показан в кружках. Оценку 2-го этапа проведем по математическому ожиданию.
Для одного состояния эта оценка  , для другого
, для другого 
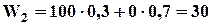 . Эти оценки помещены в квадраты. Оценка последнего этапа (1-го по нумерации): в случае профилактики выигрыш равен W1-= 60 — 20 = 40 р., без профилактики W1 = 30 р. Решение: проводить профилактику W
. Эти оценки помещены в квадраты. Оценка последнего этапа (1-го по нумерации): в случае профилактики выигрыш равен W1-= 60 — 20 = 40 р., без профилактики W1 = 30 р. Решение: проводить профилактику W 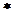 =40р.
=40р.
Пример 3. Задача о выпуске партии консервов
Фирма освоила выпуск новых консервов. Образцы прошли дегустацию и сделан вывод, что при массовом выпуске консервов в производство успешный массовый сбыт ожидается с вероятностью 0,3, при этом ожидаемая годовая прибыль 3 млн. дол., а в случае неуспеха потери составят 250 тыс. дол. Возможен вариант предварительного пробного выпуска небольшой партии товара (затраты на выпуск партии составят 50 тыс. дол.). Оценки экспертов возможных ситуаций при продаже опытной партии и вероятности успеха и неуспеха при последующем массовом выпуске даны в таблице 6.
Итак, возможны решения.
1) Отказаться от выпуска.
2) Начать сразу массовый выпуск
3) Вначале выпустить опытную партию.
Необходимо построить дерево решений и, используя метод ДП, найти лучшее из возможных решение.
Табл. 6
| События Результат массового выпуска | А) Покупают < 10% потребителей | Б) Покупают >10% вторично < 50% | В) Покупают >10% вторично >50% | 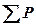
|
| Успех | 0,03 | 0,07 | 0,20 | 0,30 |
| Неуспех | 0,47 | 0,18 | 0,05 | 0,70 |
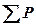
| 0,50 | 0,25 | 0,25 |
Последовательно, начиная с последнего этапа, вычисляются условные оптимумы.

Рис 7
Дерево решений имеет вид, показанный на рис 7
1) Узлы (7),(8),(9). Чтобы подсчитать максимальные значения целевой функции на 1-м шаге, необходимо знать условные вероятности – условную вероятность события «У», если имело место событие «а» (успех при m1<10%), p(У/a) и т.д.
Из таблиц п. 9.2. следует (решения «природы»).
p(У/a) = 0,03/0,5 = 0,06; p(НУ/a) = 0,47/0,5 = 0,94;
p(У/б) = 0,07/0,25 = 0,28; p(НУ/б) = 0,18/0,25 = 0,72;
p(У/в) = 0,20/0,25 = 0,8; p(НУ/в) = 0,05/0,25 = 0,2.
Соответствующие значения функций:
W7 = 3000×0,06-250×0,94 = -55 тыс.
W8 = 3000×0,28-250×0,72 = 660 тыс.
W9 = 3000×0,8-250×0,2 = 2350 тыс.
2) Принимаются решения (условные оптимумы):
— узел 4 – «отказ», W4 = 0.
— узел 5 – «МП», W5 = 660 тыс.
— узел 6 – «МП», W6 = 2350 тыс.
3) Узел 3. Решение «природы»
W3 = 0×0,5+660×0,25+2350×0,25-50 = 702,5 тыс.
4) Узел 2. Решение «природы»
W2 = 3000×0,3-250×0,7 = 725 тыс.
5) Узел 1. Выбор из трёх возможных решений делается в пользу массового производства W = 725 тыс. – наибольшая ожидаемая прибыль.
Можно отметить, что, если затраты на опытное производство будут менее 27,5 тыс., более выгодным окажется решение «начать с опытного производства».
ЛИТЕРАТУРА
1. Р. Акоф, М. Сасиени. Основы исследования операций. М., 1971.
2. Р. Акофф. Искусство решения проблем. М., 1982.
3. Бахвалов Н.С. Численные методы. М., 1975
4. С. Бир. Мы и сложность современного мира. Кибернетика сегодня: проблемы и суждения. М., 11.1976.
5. Блехман И.И., Мышкис А.Д., Пановко Я.Г. Механика и прикладная математика. Логика и особенности приложения математики. Киев, 1990.
6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М., 1980.
7. Гермейер Ю.Б. Введение в теорию исследования операций. М., 1971.
8. Грекова И. Методологические особенности прикладной математики на современном этапе её развития. //»Вопросы философии». 1976.6.
9. Грекова И. Всем ли ездить на ярмарку в Дублин? //»Знание — сила» 8. 1979.
10. Грекова И. Математика и постижение реальности. //»Наука и жизнь» 1985. 3.
11. Губанов В.А., Захаров В.В., Коваленко А.Н. Введение в системный анализ. Ленинград, 1988.
12. Дроздов Н.Д. Некоторые вопросы организации прикладных исследований. «Системы: Математические методы описания, САПР и управление». Калинин. 1989.
13. Дроздов Н.Д., Барсукова Н.Е. Динамика взаимодействия сельхозкооперативов и личных хозяйств членов этих кооперативов // Ученые записки Тверского университета. Тверь 1996.
14. Э.Квейд. Анализ сложных систем. М., 1969.
15. Клиланд Д., Кинг В. Системный анализ и управление.М.,1974.
16. Кравченко А.И. Прикладная социология и менеджмент. М.,1975.
17. Краснощеков П.С. Математические модели в исследовании операций. М., 1987.
18. Кудрявцев Л.Д. Мысли о современной математике и её изучении. М., 1977.
19. Моисеев Н.Н. Математик задает вопросы. М., 1974.
20. Моисеев Н.Н. Математик ставит эксперимент. М., 1979.
21. Моисеев Н.Н. Математические задачи системного анализа. М., 1981.
22. Моисеев Н.Н. Эффективность, устойчивость, справедливость.// «Знание — сила», 1984.3.
23. Моисеев Н.Н. Слово о научно-технической революции. М., 1985.
24. Э. Мушик, П. Мюллер. Методы принятия технических решений. М., 1990.
25. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. М., 1989.
26. Петров А.А., Поспелов И.Г., Шананин А.А. Опыт математического моделирования экономики.М.,1996.
27. Плотинский Ю.М. Математическое моделирование динамики социальных процессов. М., 1992.
28. П. Райветт, Р.Л. Акофф. Исследование операций. М., 1986.
29. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике. М., 1984.
30. Трухачев Р.И. Модели принятия решений в условиях неопределенностей. М., 1981.
31. Р. Шенон. Имитационное моделирование систем — Искусство и наука. М., 1978.
32. Исследование операций. под ред. Дж. Моудера, С. Элмаграби. М., 1981.
33. Эконометрическое моделирование. Ответственный редактор Иванилов Ю.П. М., 1992
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1154; Нарушение авторских прав?; Мы поможем в написании вашей работы!