Интервальные оценки

Распределение Стьюдента

Пусть случайная величина x распределена по стандартному нормальному закону N(0,1). Случайную величину x делят на корень из c²/k.

Закон Стьюдента – это отношение нормированной случайной величины x к квадратному корню из независимой случайной величины, распределенной по закону «Хи – квадрат» с k степенями свободы, делённой на k. Данная случайная величина и соответствующий закон распределения обозначаются через t(k), именуются «распределение Стьюдента»:

.

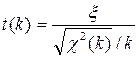(6.8)

График плотности распределения Стьюдента похож на график нормального распределения, приведённого на рис 5.4. С увеличением k – степеней свободы кривая вытягивается вдоль оси y.

Свойства распределения Стьюдента:

Свойство 1. Распределение Стьюдента симметрично относительно оси Y, причём M t(k) = 0.

Свойство 2. При больших значениях k распределение Стьюдента близко к стандартному нормальному распределению N(0,1).

В разделе 6.3 на примерах было показано определение выборочных числовых характеристик случайной величины: выборочной средней –`x, выборочной дисперсии – D_в, выборочного среднего квадратического отклонения – s_в. Полученные оценки являются приближенными. Поэтому вводится понятие интервальных оценок.

Интервальной называют оценку, которая определяется границами: началом и концом диапазона значений характеристики. Интервальные оценки позволяют установить точность и надёжность оценок. Однако граничные значения также случайные величины. Следовательно, строится интервал со случайными границами, который с заданной вероятностью содержал бы неизвестное значение параметра распределения.

Для определения погрешности полученных значений используют интервальные оценки, применяя понятие «доверительного интервала» – интервала, внутри которого параметр, как ожидается, найдется с некоторой доверительной вероятностью (надёжностью) b. Иногда вместо b используют величину a = 1 – b, называемую уровнем значимости. На практике уровнь значимости – малое число, которое принимается примерно равным:

a = 0,01; a =0,05; a = 0,1.

Дата добавления: 2014-12-27