Тема 10. Аналіз тенденцій розвитку та коливань

Ряди динаміки можуть бути представлені у вигляді суми таких складових: основної тенденції розвитку – тренду; сезонної (періодичної) компоненти; випадкової компоненти.

При аналізі рядів динаміки важливо виявити основну тенденцію розвитку (тренд) соціально-економічного явища та характер динаміки. Під загальною тенденцією динаміки розуміють тенденцію до зростання, стабільності чи зниження рівня певного явища, а під характером динаміки – ту чи іншу тенденцію зміни показників динаміки: абсолютного приросту, темпів зростання або приросту.

Інколи виявити загальну тенденцію розвитку і характер динаміки за ланцюговими показниками не вдається. Це трапляється в тих випадках, коли рівні або одержані ланцюгові показники динаміки значно варіюють, то підвищуючись, то знижуючись. У такому разі основна тенденція розвитку явища ніби затушовується. Виявлення загальної тенденції розвитку називається в статистиці вирівнюванням динамічних рядів, а методи виявлення основної тенденції – методами вирівнювання.

До методів вирівнювання динамічних рядів можуть бути віднесені такі:

а) збільшення інтервалів;

б) визначення ковзної середньої;

в) аналітичне вирівнювання.

Найбільш простим способом вирівнювання рядів є збільшення інтервалів. Суть цього підходу полягає в тому, що первинний ряд динаміки перетворюється і заміняється іншим, рівні якого відносяться до більших за тривалістю періодів часу (денні інтервали замінюються на п’яти- або десятиденні, місячні інтервали – на квартальними тощо). Знов утворений ряд буде містити збільшені рівні, отримані підсумуванням рівнів первинного ряду абсолютних величин. При цьому відхилення в рівнях, обумовлених випадковими причинами, взаємно гасяться, згладжуються і більш чітко виявляються в дії основні фактори зміни рівнів, тобто загальна тенденція.

Одним із розповсюджених простих методів вирівнювання динамічних рядів є їх згладжування за допомогою ковзної середньої. Суть методу полягає в тому, що для первинного ряду динаміки формуються збільшені інтервали, які складаються з однакової кількості рівнів т. Середній рівень обчислюється спочатку з т першихчисел ряду, потім – з т чисел ряду, але починаючи з другого, далі – починаючи з третього і т.д., тобто , , тощо. Недоліком вирівняного ряду методом ковзної середньої є те, що такий ряд «скорочується» порівняно з первинним на рівнів ряду з одного та другого кінця (п – кількість рівнів первинного ряду).

Використання в аналізі рядів динаміки способу збільшення інтервалів та методу ковзної середньої дозволяє виявити тренд для його опису, але отримати узагальнюючу статистичну оцінку тренду цими підходами неможливо. Вирішення цієї задачі – вимір тренду – досягається методом аналітичного вирівнювання. Суть аналітичного вирівнювання динамічних рядів полягає в тому, що фактичні рівні ряду замінюються плавними рівнями, обчисленими на основі певної прямої чи кривої, обраної в припущенні, що вона найточніше відображає загальну тенденцію явища. В основі методу лежить встановлення функціональної залежності рівнів ряду від часу з використанням кореляційно-регресивного аналізу. При цьому на практиці застосовуються найчастіше математичні функції такого виду:

а) лінійна ;

б) поліноміальна ;

в) гіперболічна ;

г) показова ,

д) логарифмічна ,

е) степенева

де - параметри, які знаходяться методом найменших квадратів;

- порядковий номер періоду.

Підбір функції, за допомогою якої здійснюється вирівнювання, відбувається у два етапи:

1) вибір виду функції, яка дає найкраще наближення;

2) визначення параметрів вибраної функції.

Щоб підібрати вид функції, яка давала б найкраще наближення теоретичної лінії до емпіричних даних, слід виходити з економічної суті досліджуваних залежностей. Зокрема:

1) якщо динаміка характеризується більш-менш стабільним абсолютним приростом, використовується рівняння прямої лінії (рис. 10.1);

t

Y

t

Y

Рисунок 10.1 – Лінійна форма тренду

2) вирівнювання динамічних рядів за рівнянням параболічної функції необхідно використовувати у тих випадках, коли зміна рівнів ряду відбувається з приблизно рівномірним темпом зросту або уповільненням ланцюгових абсолютних приростів, тобто коли

(рис. 10.2)

Рисунок 10.2 – Параболічна форма тренду

3) Гіперболічна форма тренду підходить для відображення тенденції чи процесів, які обмежені граничним значенням рівня (рис. 10.3).

Рисунок 10.3 – Гіперболічна форма тренду

4) Показова форма тренду відображає тенденцію прискореного та більш прискореного зростання рівнів. Такий характер має, наприклад, розмноження організмів при відсутності обмежень з боку середовища: бур’янів, хижаків, вірусних захворювань (рис. 10.4):

Рисунок 10.4 – Степенева форма тренду

У практичній діяльності може виникнути необхідність інтерполяції або екстраполяції рядів динаміки

Інтерполяція – це знаходження відсутніх проміжних рівнів ряду. Знаючи рівняння тренду для обчислення теоретичних рівнів і підставляючи в нього проміжне значення t між заданими, можна визначити йому відповідний теоретичний рівень результативного фактору .

Екстраполяція використовується при прогнозуванні явищ у майбутньому з припущення, що виявлена тенденція буде зберігатися і надалі за межами досліджуваного ряду динаміки. При цьому значення t за межами динамічного ряду підставляють у трендові рівняння і отримують точкове прогнозне значення рівня тренду у майбутньому.

На практиці результат екстраполяції прогнозованих соціально-економічних явищ звичайно виконують інтервальними оцінками. Для визначення меж інтервалів використовується інтервальна нерівність:

, (10.1)

де - коефіцієнт довіри за розподілом Ст’юдента;

- залишкове середнє квадратичне відхилення:

, (10.2)

де - кількість рівнів ряду, - кількість параметрів теоретичної залежності тренду;

- значення і -го рівня ряду, що знайдено за аналітичним рівнянням;

- статистичне значення і -го рівня ряду;

- точкове значення прогнозного рівня, що знайдено за аналітичним рівнянням.

Коефіцієнт довіри обирається із статистичних таблиць розподілу Ст’юдента залежно від числа ступенів вільності (n-m) і рівня значимості (0,01 або 0,05) (додаток А). Тоді остаточно з імовірністю прогнозний рівень тренду у майбутньому буде знаходитись у межах від () до ().

Приклад. На підставі даних про продаж продукції за останні десять років маркетинговий відділ має визначити основну тенденцію продажу та визначити прогнозні показники на 2001 та 2002 роки.

1. Визначити параметри рівняння для розрахунку прогнозних показників.

2. Визначити значення прогнозу та діапазон можливого відхилення на 2001 та 2002 рр.

Дані для розв’язання задачі наведені в таблиці 10.1.

Таблиця 10.1 – Початкові дані

Роки
Обсяг продажів

Для виявлення основної тенденції необхідно провести вирівнювання рядів динаміки методом ковзної середньої при т=5.

Метод простої ковзної середньоїдля перших т=5 рівнів ряду розраховується їх середня арифметична.

, і т.д.

На підставі даного ряду в цій задачі ковзну середню наведено в таблиці 10.2 та на рис. 10.5:

Таблиця 10.2 – Значення ковзної середньої

Роки
Ковзна середня			88,4		93,6		95,6	97,6

Рисунок 10.5 – Статистичні дані та ковзна середня

Очевидно, що продаж продукції має тенденцію до зростання.

З метою прогнозування необхідно здійснити аналітичне вирівнювання. Для визначення форми тренда зобразимо дані графічно (рис. 10.6).

Очевидно, загальна тенденція має лінійну форму .

Для визначення параметрів рівняння регресії скористаємося формулами за методом найменших квадратів.

Рисунок 10.6 – Графічне зображення статистичних даних.

Параметри моделі розраховуються в результаті розв’язання системи нормальних рівнянь, використовуючи метод найменших квадратів:

(10.3)

або:

. (10.4)

Для цього виконаємо ряд розрахунків (табл. 10.3).

Таблиця 10.3 – Розрахункові дані

ti	yi	yi*ti	ti^2
t^ср = 5.5	= 93	Σ = 5254	Σ = 385

Динамічна модель має вид .

Використаємо дане рівняння для вирівнювання рівнів ряду динаміки (табл. 10.4) та наведемо графічно статистичні дані та значення, що розраховані за формулою (рис. 10.7).

Таблиця 10.4 – Модельні та статистичні значення показника

ti	yi	y(t)

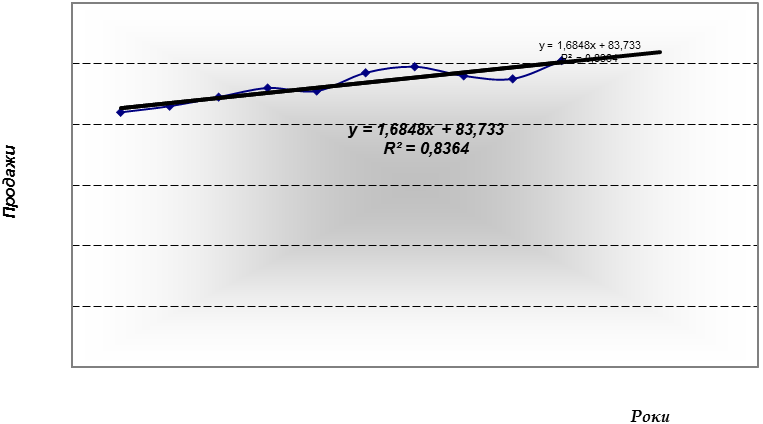
Рисунок 10.7 – Графічне зображення статистичних даних та даних регресії

Використовуючи дану модель можна розрахувати прогнози на 2001 та 2002 роки (табл. 10.5).

Таблиця 10.5 – Розрахункові дані

Роки	ti	Обсяг продажів (yi)	Розрахункові значения за моделлю, y(t)	(yi- y(t))^2
Разом

Довірчий інтервал: ,

t_α - табличне значення t- критерію Ст’юдента (при рівні значимості 0,05 та n =8) = 2,31 (Додаток А).

Таким чином, величина довірчого інтервалу коливається в межах від (102-5,29) до (102+5,29), тобто з імовірністю 0,95 прогнозне значення продаж на 2001 рік буде знаходитися в межах .

Поквартальні або помісячні рівні багатьох показників соціально-економічних явищ суттєво залежать від сезонності (сезонних коливань), тобто від більш-менш постійно повторюваних із року в рік коливань рівнів динаміки. У більшості випадків ці коливання повв’язані зі зміною пори року.

У статистиці існує ряд методів вивчення та виміру сезонних коливань:

а) метод абсолютних різниць;

б) метод відносних різниць;

в) побудова індексів сезонності;

г) побудова аналітичної моделі.

За методом абсолютних різниць сезонні коливання характеризуються величинами:

або , (10.5)

де - абсолютні відхилення фактичних рівнів або середніх місячних (квартальних) рівнів за кілька років () від загальної середньої () або трендового і -го рівня .

За методом відносних різниць сезонні коливання описуються залежністю:

або . (10.6)

Графічне зображення абсолютних або відносних різниць рівнів за місяцями (кварталами) року наочно ілюструють сезонну хвилю.

Замість відносних різниць за кожен місяць може бути розрахований індекс сезонності,що визначається як відношення середнього рівня відповідного місяця до загальної середньої:

. (10.7)

Індекси сезонності можуть бути розраховані і як відношення фактичного рівня відповідного місяця до рівня, розрахованого за рівнянням тренду.

Загальним показником сили коливання динамічного ряду сезонності за рік є середнє квадратичне відхилення індексів сезонності, виражене в процентах:

. (10.8)

Чим менша величина цього показника, тим меншою є сезонність досліджуваного явища.

Приклад. Є дані про динаміку постачання молока (т) за три роки для молокозаводів міста (табл.10.6). Потрібно визначити індекси сезонності, зобразити сезонну хвилю постачання молока графічно. Зробити висновки.

Таблиця 10.6 – Початкові дані

Місячні дані одного року через вплив випадкових факторів можуть бути нетиповими для виявлення тенденції розвитку явища. Тому доцільно визначити індекси сезонності в середньому за три роки. Спочатку для кожного місяця за три роки обчислимо середню величину постачання молока. Потім визначимо середньорічний рівень для триріччя та обчислимо індекси сезонності (табл. 10.7):

Середні рівні постачання молока за три роки за місяцями: .

У січні т.

У лютому т. і т.д.

Таблиця 10.7 – Розрахункові дані

За обчисленими середньомісячними рівнями визначимо загальний середній рівень за три роки: т.

Або за даними про середні рівні за кожен рік:

т.

Встановимо індекси сезонності постачання молока: .

У січні

У лютому і т.д.

Зобразимо сезонну хвилю постачання молока (рис. 10.8).

Рисунок 10.8 – Сезонна хвиля постачання молока на молокозаводи міста

З даних таблиці та рисунку видно, що сезонність постачання молока на молокозаводи міста має чітко виражений характер: найбільше молока було поставлено у весняно-літній період, а найменше – в осінньо-зимовий. Максимум постачання припадає на грудень.

Загальна середньомісячна сила коливання постачання молока:

Таким чином, кожний місяць відхилення споживання молока від седньомісячного рівня в 153,8 т у середньому складає 17,1 %.

Дата добавления: 2014-12-23