
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамические структуры данных 3 страница
|
|
|
|
Процедура dispose освобождает участок памяти точно такой же протяженности, как у предоставленного когда-то процедуре New. Разумеется, впоследствии этот участок может пойти в дело при условии, что программе понадобится новое пространство такого же или меньшего размера. Сама Паскаль-система не предпринимает каких-либо автоматических действий по "сборке мусора", то есть такой организационной процедуре, которая обнаруживала бы все разрозненные кусочки никем не используемой памяти и объединяла их в одной непрерывной области.
В качестве компромисса Паскаль предлагает две стандартные процедуры, позволяющие управлять распределением динамической памяти крупными блоками, а не минимально необходимыми порциями, как это происходит при работе с New и Dispose. Они называются Mark (пометить) и Release освободить). Применять их в рамках одной программы совместно с dispose нельзя.
Текущая граница незанятой динамической памяти хранится в переменной-указателе HeapPtr. Процедура Mark запоминает значение указателя HeapPtr. После этого, используя процедуру Release, можно в любой момент освободить динамическую память, начиная с запомненного процедурой Mark адреса. Рассмотрим пример:
Program Ex32;
Var
Ptr:pointer;{Объявление пеpеменной типа Pointer
для использования в пpоцедуpе Mark}
P1,P2,P3,P4:^Byte;
Begin
New(P1); New(P2);
P2^:=1;
Mark(Ptr);{Запоминание значения HeapPtr}
New(P3);
P3^:=0;
Writeln(P2^); Writeln(P3^);
{Освобождение памяти, начиная с адpеса пеpеменной P3^}
Release(Ptr);
New(P4);
P4^:=2;
Writeln(P2^);
{Обpащение к P3^ пpиведет к получению значения 2}
Writeln(P3^)
End.
В результате выполнения этой программы на экран будет выведено сначала 1 и 0, а затем 1 и 2.
Работа с динамической памятью предъявляет к программисту ряд требований. Во-первых, желательно освобождать выделенные области памяти сразу же после того, как необходимость в их использовании отпадает. Во-вторых, сразу же после освобождения памяти следует соответствующему указателю присваивать значение Nil.
Указатели и динамические переменные в практике программирования на Паскале находят исключительно широкое применение как основа для построения весьма сложных информационных структур, которые будут подвергнуты рассмотрению далее.
9.6. Понятие и характеристики информационных структур
Для каждого круга задач характерны определенные структуры данных, над которыми выполняются алгоритмические действия.
В реальной среде, в которой протекают процессы, отображаемые алгоритмом, элементы данных связаны некоторыми формами взаимного влияния или взаимной зависимости. Например, если среда представляет собой металлическую пластинку, то между ее элементами, являющимися пространственными соседями, передается теплота. Если это телефонная сеть, то аппараты связаны с подстанциями, подстанции со станциями, станции между собой и т.д. Разумеется, обычно нельзя отобразить все связи реальной среды. Поэтому нужно выбирать связи, существенные для данного процесса, отбрасывая остальные, получая таким образом упрощенную модель среды.
Связанные между собой элементы данных образуют структуру данных или информационную структуру.
Каждая информационная структура характеризуется:
· взаимосвязью элементов;
· набором типовых операций над этой структурой.
Сравните с определением элемента данных: каждый элемент данных относится к одному из конечного множества типов. Тип – это множество значений, которые могут принимать объекты программы, и совокупность операций, допустимых над этими значениями.
В простейшей форме структура данных может быть линейным списком элементов. Тогда присущие структуре свойства содержат в себе ответы на такие вопросы: какой элемент является первым в списке? какой - последним? какой элемент предшествует данному или следует за данным?
В более сложных ситуациях информационная структура может быть двумерным массивом (т.е. матрицей, иногда называемой сеткой, имеющей структуру строк и столбцов), либо может быть n-мерным массивом при весьма больших значениях n, либо она может иметь структуру дерева, представляющего отношения иерархии или ветвления, либо это может быть сложная многосвязная структура с огромным множеством взаимных соединений, такая, например, которую можно найти в человеческом мозге.
Чтобы правильно использовать машину, важно добиться хорошего понимания структурных отношений, существующих между данными, способов представления таких структур в компьютере и методов работы с ними.
Как правило, набор типовых операций над информационными структурами в основном состоит из операций выборки, записи и поиска.
Нет ничего мистического, таинственного или трудного в методах работы со сложными структурами; эти методы являются важной частью репертуара каждого программиста. Для реализации некоторой структуры на Паскале необходимо отобразить ее на одну из структур Паскаля и написать на Паскале процедуры выполнения типовых операций.
9.6.1. Очереди. Стеки
Очередь – одна из простейших и в то же время достаточно типичная структура данных, потребность в которой возникает при программировании реальных процессов и ситуаций. Необходимость в очереди возникает, когда имеется некоторый механизм обслуживания, который может выполнять заказы последовательно, один за другим.
 |
Если при поступлении нового заказа обслуживающее устройство свободно, оно может немедленно приступить к его выполнению, но если оно уже выполняет некоторый ранее полученный заказ, то новый заказ должен поступить в конец очереди заказов, ожидающих выполнения. Каждый раз, когда обслуживающее устройство завершает выполнение текущего заказа, оно приступает к выполнению заказа из начала очереди, причем этот заказ удаляется из очереди и первым в очереди становится следующий за ним заказ. Если заказы поступают нерегулярно, их очередь то удлиняется, то укорачивается, и время от времени может становиться пустой, когда все имеющиеся заказы выполнены, а новые еще не поступили.
Left Right
Рис. 9.2 Типовое представление очереди
Очередь, как структура данных, используется, например, для моделирования реальных очередей с целью определения их характеристик (средняя длина очереди, время пребывания заказа в очереди, вероятность отказа в постановке в очередь при ограничении ее максимальной длины и т.п.) при данном законе поступления заказов и дисциплине их обслуживания.
По своему существу очередь является сугубо динамическим объектом - с течением времени и длина очереди и набор образующих ее элементов изменяются.
Для простоты предположим, что каждый заказ кодируется некоторым целым числом. В таком случае очередь организуется из чисел, представляющих собой коды заказов. Например, исходная очередь могла бы состоять из чисел 59 и 17. Потом из очереди выбирается первое число 59, и в ней остается единственный элемент 17. Если далее в очередь последовательно поступают числа 31 и 7, то теперь очередь имеет вид: 17, 31, 7.
Над очередью могут выполняться операции двух видов:
1) выборка с одновременным удалением из очереди первого ее элемента;
2) занесение нового элемента в конец очереди.
Опишем реализацию очереди на Паскале.
Пример:
Program Ex33;
Type PQuery = ^Query;
Query = record
Inf: integer;
Next: PQuery;
end;
Var Left, Right, E, Final: PQuery;
I, V: integer;
Begin
Read(v); {v-целое число в инф. части 1-го элемента очереди}
I:=1;
writeln(i,'-й эл-т очереди = ',v);
if v=999 then exit;
new(E);
E^.inf:=v;
E^.next:=nil;
Left:=E; Right:=E;
while true do
begin
Read(v);
inc(i);
writeln(i,' эл-т очереди = ',v);
if v=999 then exit; {999 - признак конца ввода данных}
new(E);
E^.inf:=v;
E^.next:=Left;
Left:=E;
end;
goto m;
end.
 E E E
E E E
…
Left Left Left Right
Рис. 9.3 Организация очереди
Добавление нового элемента в очередь запишем в виде процедуры.
Procedure AddEQuery;
Begin
Read(v);
If v=999 then Exit;
New(E);
E^.inf:= v;
E^.next:= nil;
Right^.next:= E;
Right:= E;
End;
 |
E E E E
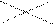 |
Left Right Right
Рис. 9.4 Добавление элемента в очередь
Оформляя типовые операции над структурами данных в виде паскалевских процедур, мы получаем возможность в дальнейшем писать на Паскале программу, оперирующую новыми структурами, не задумываясь над тонкостями их реализации, а просто включив в свою программу описания этих процедур и обращаясь к ним в тех местах, где возникает потребность в операциях над такими структурами.
Удаление из очереди первого элемента процедурой:
Procedure DelEQuery;
Begin
Final:= Left;
Left:= Left^.Next;
Dispose(Final);
end;
E E E

Final Left Left Right
Рис. 9.5 Удаление элемента из очереди
Приведенные процедуры не содержат контроля правильности обращения к ним. В частности, если очередь пустая, то выполнение процедуры DelEQuery приведет к присваиванию переменной Next постороннего значения. Ответственность за правильные обращения к таким процедурам полностью ложится на человека, пользующегося ими.
Различают два основных вида очередей, отличающихся по дисциплине обслуживания находящихся в них элементов. Дисциплину обслуживания, которую мы только что рассмотрели принято называть FIFO (First In - First Out, то есть первый пришел - первый вышел). Надо отметить, что очереди с такой дисциплиной обслуживания используются в программировании относительно редко. Теперь мы остановимся на очереди с такой дисциплиной обслуживания, при которой на обслуживание первым выбирается тот элемент очереди, который поступил в нее последним. Эту дисциплину обслуживания принято называть LIFO (Last In - First Out, то есть последним пришел - первым вышел). Очередь такого вида в программировании принято называть стеком (механизмом магазиной памяти) - это одна из наиболее употребительных структур данных, которая оказывается весьма удобной при решении различных задач.
Условно стек в памяти можно представить следующим образом:

 1 – нижняя граница стека;
1 – нижняя граница стека;
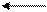
 3 2 – верхушка стека;
3 2 – верхушка стека;
 3 – верхняя граница стека.
3 – верхняя граница стека.
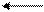 2 Если в ходе добавления элементов в стек,
2 Если в ходе добавления элементов в стек,
1 
 указатель вершины стека достигает верхней границы, то возникает переполнение стека.
указатель вершины стека достигает верхней границы, то возникает переполнение стека.
Если в ходе исключения элементов достигнута нижняя граница стека, то возникает антипереполнение стека. В случае переполнения или антипереполнения стека происходит аварийное завершение программы.
Стек представляет собой последовательность элементов, упорядоченных по времени их поступления, причем извне доступна только вершина стека, то есть место, в котором находится последний по времени поступления элемент. Обратиться к стеку можно для того, чтобы забрать элемент из вершины или добавить в него новый элемент. Стек можно сравнить со стопкой бумаги, накапливающейся на письменном столе. Когда мы забираем элемент из вершины, то новой вершиной стека становится предыдущий по времени поступления элемент. Когда мы добавляем новый элемент, то он как бы ложится поверх прежней вершины, и теперь уже становится вершиной стека.
Над стеком могут выполняться операции:
1) организация стека;
2) удалением элемента из стека;
3) занесение нового элемента в стек;
4) просмотр или обработка стека.
Опишем реализацию стека на Паскале.
Пример:
Program Ex34;
type PStack = ^Stack;
Stack = record
inf: integer;
next: PStack;
end;
var UpStack, E, NE, Temp: PStack;
v,i: integer;
Begin
Read(v); {v-целое число в инф. части 1-го элемента стека}
I:=1;
writeln(i,'-й эл-т стека = ',v);
if v=999 then exit; {999 - признак конца ввода данных}
UpStack:= nil; {верхушка стека пуста}
new(E);
E^.inf:= v;
E^.next:= UpStack;
UpStack:= E;
while true do
begin
Read(v); inc(i);
writeln(i,'-й эл-т стека = ',v);
if v=999 then exit; {999 - признак конца ввода данных}
if i>=999 then
begin writeln('ПЕРЕПОЛНЕНИЕ!!!!!!!!');
HALT(1); end;
new(E); E^.inf:= v; E^.next:= UpStack;
UpStack:= E;
end;
 end.
end.
E E E
UpStack
UpStack UpStack UpStack
Рис. 9.6 Организация стека
Добавление нового элемента в стек запишем в виде процедуры.
Procedure AddEStack;
Begin
Read(v); inc(i);
writeln(i,'-й эл-т стека = ',v);
if v=999 then exit; {999 - признак конца ввода данных}
if i>=999 then
begin writeln('ПЕРЕПОЛНЕНИЕ!!!!!!!!');
HALT(1); end;
new(NE);
NE^.inf:= v;
NE^.next:= UpStack;
UpStack:= NE;
End;
Для того чтобы удалить элемент из стека, необходимо указатель верхушки стека переместить на предыдущий элемент стека. После чего очистить ячейку памяти с данными верхушки стека. Реализуем эти действия в процедуре DelEStack.
Procedure DelEStack;
Label m1, m2;
Var b: char;
Begin
m2: Writeln(‘Вв. «Д», если хотите продолжить удаление эл-в’);
Writeln(‘или «Н» в противном случае’);
Read(b);
If (b=’Н’) or (b=’н’) then goto m1 else
If (b=’Д’) or (b=’д’) then
While UpStack<>Nil do
Begin
NE:= UpStack;
UpStack:= E^.Next;
Dispose(NE);
End;
Goto m2;
m1:
End;
Следующий пример иллюстрирует организацию стека, используя статические типы данных.
Пусть массив Т содержит арифметическое выражение, записанное с помощью букв, знаков операций и круглых скобок. Например, выражение x+(y*(y-x)+(a-b)/x-y)/a. разместится в массиве Т так: T[1]='x',T[2]='+', T[3]='(' и так далее. Признаком конца выражения служит точка.
Каждому символу выражения ставится в соответствие его индекс в массиве Т. Задача состоит в том, чтобы найти все пары скобок () и построить таблицу В, в которой для каждой такой пары скобок должна быть строка с указанием координат открывающей скобки и соответствующей ей закрывающей. Для приведенного примера в таблице В должны быть пары: 5,9; 11,15; 2,20.
Продвигаясь по тексту выражения Т слева направо, мы можем образовывать очередь координат открывающих скобок, ожидающий соответствующих закрывающих скобок. Особенность этой очереди состоит в том, что каждый раз, когда встретится закрывающая скобка, она будет соответствовать той открывающей скобке из очереди, которая появилась там самой последней. Для реализации такой очереди и употребляется стек.
В случае этой задачи каждый элемент стека является одиночным числовым значением. Такой стек легко отобразить на одномерный массив S. Операция занесения в стек (то есть в вершину стека) значения x будет реализовываться процедурой InStek(S,x); операция извлечения из стека (то есть из его вершины) хранящегося там значения будет реализовываться процедурой OutStek(S,x), где x - имя переменной, в которую занесется значение, извлекаемое (и одновременно удаляемое) из стека. Массив S будет начинаться с элемента S[0], который служит указателем свободного места в стеке, то есть содержит индекс того элемента массива, который следует за текущей вершиной стека. Самый давний по времени поступления элемент стека хранится в массиве S в элементе S[1], а поступившие позднее элементы стека хранятся в массиве S соответственно в его элементах S[2], S[3],...,S[S[0]-1]. Если стек пуст, то S[0]=1. Процедуры InStek и OutStek описываются на Паскале следующим образом:
Procedure InStek(Var S:Stek; x:integer);
Begin S[S[0]]:=x; S[0]:=S[0]+1 end;
Procedure OutStek (Var S:stek; x:integer);
Begin S[0]:=S[0]-1; x:=S[S[0]] end;
Предполагается, что тип Stek описан следующим образом:
Type Stek = array[0..m] of integer;
Процедура InStek начинает работу с того, что заносит значение x в вершину стека, индекс которой в массиве S указывается значением S[0]. После этого первым свободным становится следующий элемент массива S с индексом S[0]+1. Это новое значение индекса первого свободного элемента заносится в S[0].
Процедура OutStek уменьшает S[0] на 1, то есть передвигает указатель стека на последний занятый элемент стека, а затем выбирает оттуда значение и передает его в x.
Уточним теперь постановку задачи построения таблицы соответствия скобок. Анализируемое выражение записано в массиве Т последовательно, символ за символом. Требуется построить двумерный массив В, в котором каждая строка содержит два числа: индексы элементов массива Т для пар скобок - открывающей и соответствующей ей закрывающей. Признаком конца выражения в Т служит точка.
Приведем сначала неформальное описание алгоритма.
1. Образовать пустой стек S и подготовиться к формированию первой строки массива В.
2. Перебирать последовательно от начала все элементы массива Т, пока не встретится признак конца выражения. Если в очередном элементе T[k] встретится код символа '(', то индекс этого элемента занести в стек. Если же в очередном элементе T[k] встретится код символа ')', то сформировать очередную i-ю строку массива В, в которую занести, во-первых, значение из вершины стека (индекс элемента массива Т, содержащего код символа '(', и во-вторых, индекс k. Тем самым получаются координаты очередной пары скобок.
Программа, реализующая данный алгоритм:
Program Ex35;
Const Lb =20;{длина В}
m=10; {длина S}
Lt = 100;{длина T}
Type Stek =array [0..m] of integer;
Var S:stek;
B:array[1..Lb,1..2] of integer;
T:string[lt];
i,j,k:integer;
Procedure InStek(Var S:stek; x:integer);
Begin S[S[0]]:=x; S[0]:=S[0]+1 end;
Procedure OutStek(Var S:stek; x:integer);
Begin S[0]:=S[0]-1; x:=S[S[0]] end;
Begin
Read(t);{ Ввод массива Т}
S[0]:=1; {обpазуется пустой стек S}
i:=1; {нoмеp пеpвой свободной стpоки в массиве В}
k:=1; {номеp пеpвого символа в массиве Т}
Repeat
if T[k]='(' then
begin InStek (S,k); B[i,1]:=k;writeln(b[i,1]) end
else if T[k]=')' then
begin
OutStek(S,k);
B[i,2]:=k;
writeln(b[i,2]);
i:=i+1
end;
k:=k+1
Until T[k]='.';
For j:=1 to i-1 do writeln(B[j,1]:3, B[j,2]:3)
end.
Программа, проверяющая баланс скобок в заданной строке. Процедуры работы со стеком используют указатели.
program Ex36;
{Пpовеpка баланса скобок}
Type
Te=char;
Sv=^Zs;
Zs=record sled:Sv;
elem:Te
end;
Stek=Sv;
Var sym:char;
s:stek;
b:boolean;
Procedure Instek (Var St:stek; NewElem:Te);
Var q:Sv;
Begin
{Создание нового звена}
New(q); q^.elem:=NewElem;
{Созданное звено сделать веpшиной стека}
q^.sled:=st; st:=q
end { пpоцедуpы InStek};
Procedure OutStek(Var St:stek; Var a:Te);
Begin {a:= значение из веpшины стека}
a:=st^.elem;
{Исключение пеpвого звена из стека}
st:=st^.sled
end {пpоцедуpы OutStek};
Function Sootv:boolean;
Var r:char;
Begin
OutStek(s,r);
If sym=')' then Sootv:=r='(';
end; {функции соответствия}
Begin {фоpмиpование пустого стека}
s:=nil;
{sym:=пеpвая литеpа стpоки; b:=true}
Read(sym); b:=true;
While(sym<>'.') and b do
begin
{печать введенной литеpы}
write (sym);
if sym='(' then InStek(s,sym)
else if sym=')' then
begin
if {стек пуст или скобки не соответствуют}
(s=nil)or(not sootv) then b:=false
end;
read(sym) {ввести очеpедную литеpу}
end; {обpаботки литеp стpок}
writeln;
if{было несоответствие скобок или стек не пуст}
not b or (s<>nil)
then writeln('баланса скобок нет')
else writeln('баланс скобок есть')
end.
Одной из разновидностей однонапрвленных списков являются деки. Деки – линейные списки, добавление и исключение элементов в которых производится с двух сторон. Поэтому процедуры работы с деками аналогичны процедурам работы со стеками, только необходимо указывать с какого конца идет обращение к такому списку.
9.6.2. Списки
Список - это упорядоченный набор объектов произвольных размера и природы. Такие объекты называются записями. Упорядоченность записей определяется программистом и зависит от назначения списка. Понятие списка естественно обобщает привычные нам по повседневной жизни такие структуры, как список абонентов телефонной сети, каталог книг в библиотеке, список сотрудников учреждения и т.д. Основными операциями над списками являются переход к соседней записи, включение новой записи, исключение записи.
Списками, в общем смысле, являются рассмотренные нами структуры строки, очереди и стека. Однако в очереди и стеке доступны только краевые записи (первая или последняя по времени поступления), а в строке объектами (записями) являются только отдельные символы. Общая структура списка не предусматривает подобных ограничений.
Заметим, прежде всего, что рассмотренный нами ранее структуриро-ванный тип данных - строка, есть не что иное, как программный объект, представляющий собой последовательность символов из некоторого алфавита. К строкам применяют ряд операций, для которых в языке Паскаль предусмотрены стандартные процедуры и функции, такие как удаление одного или нескольких символов строки, вставка одного или нескольких символов в строку, поиск вхождения в строку заданной подстроки. Рассмотренный нами простейший способ представления строк называется векторным представлением, когда каждый символ строки кодируется целым числом, и эти коды располагаются в одномерном массиве подряд друг за другом. При таком представлении локальное изменение строки, касающееся одного ее символа, влечет за собой необходимость перемещения многочисленных последующих символов. Это является основным недостатком векторного представления строк. Причина этого состоит в том, что в векторе понятие "следующий элемент" связывается с местом расположения предыдущего элемента. Такое представление, как правило, плохо пригодно для структур, которые меняются в середине, хотя оно вполне удовлетворительно для структур, меняющихся только по краям (таким, как очередь или стек).
9.6.2.1. Представление строки в виде цепочки
Между тем совсем необязательно жестко связывать место расположения (т.е. индекс) следующего символа с индексом предыдущего. Можно располагать символы в любом порядке, но при этом каждый символ придется сопровождать указанием места расположения следующего. При таком отображении строки на одномерный массив каждому символу строки ставится в соответствие пара соседних между собой элементов массива: в одном записывается код самого символа, а в другом - ссылка на следующую пару, т.е. индекс первого элемента пары, в котором записан следующий символ.
Каждая такая пара элементов массива называется звеном. Последовательные ссылки друг на друга сцепляют звенья в одну цепочку.
Такой способ отображения структуры данных называется сцеплением. Он применяется не только для представления строк. При представлении любой структуры данных звено всегда состоит из двух частей. В первой части находится ссылка (или несколько ссылок) на соседние звенья. Она называется справкой. Во второй части располагается сам элемент структуры данных. Она называется информационной частью или телом звена.
Звенья цепочки мы можем размещать в одномерном массиве, каждое звено занимает два соседних элемента массива, но допускается любой разброс этих звеньев по массиву, так как следование определяется не номерами индексов, а значениями ссылок. Примем соглашение, что последнее звено содержит ссылку "нуль".
Пусть например, строка представляется цепочкой, состоящей из трех звеньев. Мы можем разместить первое звено в элементах массива S[2] и S[3], второе звено - в элементах S[4] и S[5] и третье звено - в элементах S[6] и S[7]. Однако можно сделать и по-другому: первое звено разместить в элементах S[75] и S[76], второе – в S[31] и S[32], третье - в S[103] и S[104]. Если рассматривать эту цепочку, что совершенно неважно, чем заполнены остальные элементы массива, и в частности, находящиеся между нашими звеньями. Теперь, чтобы включить или исключить символ, в строке ничего не нужно сдвигать: достаточно поменять некоторые ссылки.
Для того, чтобы избежать нестандартной работы с первым звеном цепочки, удобно ввести фиктивное заглавное звено и хранить его всегда в постоянном месте. В отображении строки на паскалевский массив S заглавное звено цепочки будет занимать начальные элементы S[0] и S[1]. В S[0] мы поместим ссылку на первый элемент первого звена цепочки, а в S[1] для удобства включения новых символов - значение индекса первого свободного элемента массива S.
9.6.2.2. Однонаправленные, двунаправленные и кольцевые списки
Строка, представленная в виде цепочки, является частным случаем динамической структуры, называемой в программировании линейным однонаправленным списком. В общем случае строки информационными элементами списка могут быть значения любого типа: вещественные числа, массивы, записи и т.д. Принцип организации отдельных элементов в единую структуру данных - линейный однонаправленный список - тот же самый, что и в случае строки-цепочки: каждый информационный элемент, входящий в очередное звено списка, снабжается ссылкой на следующее за ним звено. В один список принято объединять однотипные элементы.
Однонаправленный список предназначен для того, чтобы просматривать его в одном направлении, от начала к концу. Он представляется в виде цепочки, в которой справка каждого звена состоит из двух значений. Первым значением является длина звена, которая складывается из длины записи и длины справки, равной 2. Вторым значением является ссылка на начало следующего звена. Далее следует тело звена (запись).
Заглавное звено состоит из трех значений:
| Длина звена |
| Cсылка на начало первого звена |
| Ссылка на начало свободного места |
Первые два значения образуют справку заглавного звена, а ссылка на свободное место представляет собой тело этого звена. В справке последнего звена ссылка равно нулю.
Заметим, что рассмотренное ранее представление строки в виде цепочки фактически является представлением однонаправленного списка, в котором все записи содержат по одному значению, и за ненадобностью в справках отсутствуют указания о длинах звеньев (поскольку все звенья занимают стандартно по два элемента массива).
Однонаправленный список можно отобразить на одномерный массив S следующим образом. Заглавная запись будет занимать элементы S[0], S[1] и S[2]. Далее размещаются основные записи.
Если индекс звена, содержащего запись x, равен i, то в элементе S[i] находится длина этого звена, в элементе S[i+1] - индекс звена со следующей записью списка (или нуль, если запись x – последняя). Далее, начиная с элемента S[i+2], содержится сама запись x.
Включение записи в список. Пусть i - индекс звена, после которого нужно включить новую запись. Новое звено помещается в массив S на свободное место, указываемое значением S[2]. Таким образом, справка нового звена занимает в массиве S элементы с индексами S[2] и S[2]+1. В первый из них - элемент S[S[2]] – заносится значение длины нового звена. В следующий элемент - S[S[2]+1] – нужно занести ссылку на звено, которое прежде следовало за звеном с индексом i, т.е. нужно переписать туда S[i+1]:
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 436; Нарушение авторских прав?; Мы поможем в написании вашей работы!