Динамические структуры данных 4 страница

S[S[2]+1]:=S[i+1].

Далее расположится сама включаемая запись (тело нового звена). Само же звено с индексом i должно быть теперь сцеплено со вновь включенным звеном, и поэтому мы заносим в его справку индекс нового звена, равный S[2]: S[i+1]:=S[2].

Пусть новая запись хранится в массиве Inf и занимает n элементов этого массива. В массиве S новое звено вместе со своей справкой займет (n+2) элемента. Поэтому в начало его справки (в элемент S[S[2]]) мы заносим значение n+2. Теперь свободная часть массива S начинается за новым звеном и нужно заменить значение указателя первого свободного элемента: S[2]:=S[2]+n+2.

Напишем соответствующую процедуру InSpisok. Цикл в теле процедуры служит для перенесения элементов массива Inf в массив S. Для наглядности вводится вспомогательная переменная new, в которую помещается индекс S[2] начала нового звена.

Type Spisok = array [0..m] of integer;

TypeInf= array [0..l] of integer;

Procedure InSpisok (Var S:Spisok; var Inf:TypeInf; n,i:integer);

Var new, j:integer;

Begin new:=S[2]; S[new]:=n+2; S[new+1]:=S[i+1];

For j:=1 to n do S[new+1+j]:=Inf[j];

S[i+1]:=new; S[2]:=S[2]+n+2

End;

Исключение записи из списка. Пусть задано значение i, и нужно исключить из списка запись, которая содержится в звене, следующем за звеном с индексом i. Индекс исключаемого звена равен значению S[i+1]. Исключение сводится к изменению этого значения и аналогичному изменению ссылки при исключении символа из строки. Иначе говоря, значение S[i+1] заменяется на значение, которое хранилось в ссылочной части справки исключаемого звена.

Для наглядности введем переменную sled, значением которой будет индекс звена, следовавшего за звеном с индексом i: sled:=S[i+1]. Тогда исключение записи сводится к выполнению присваивания S[i+1]:=S[sled+1]. (Эта пара операторов эквивалентна одному оператору S[i+1]:=S[S[i+1]+1]).

Соответствующая процедура записывается так:

Procedure OutSpisok (Var S:Spisok; i:integer);

Var sled:integer;

Begin sled:=S[i+1]; S[i+1]:=S[sled+1] end;

Как и в случае исключения символа из строки, убираемое из цепочки звено остается в массиве S.

Поскольку первые элементы заглавного звена оформляются так же, как справка любого звена (длина и ссылка), то процедуры включения и исключения выполняются правильно и при значении i=0, т.е. при включении или исключении первой записи списка.

Когда записи исключаются из списка, возникает вопрос об использовании места хранения этих уже ненужных записей. Если все записи имеют одинаковую длину, то вновь включаемые записи можно помещать на место исключенных; для этого из исключенных звеньев обычно образуется специальный список свободных звеньев. Если же длины записей разные, то проблема использования образующихся пустот оказывается довольно сложной. Один из способов ее решения состоит в том, чтобы время от времени образовывать на новом месте копию списка, последовательно включая в нее только те записи, которые фактически присутствуют в списке.

Рассмотренные выше однонаправленные списки предусматривают жесткий порядок перебора записей - от первой к последней. Бывает так, что возникает потребность не только двигаться вперед по списку, но и возвращаться назад, чтобы посмотреть, а возможно, и изменить содержимое предыдущих записей. Эту возможность обеспечивает структура двунаправленного списка.

Такой список представляется в виде цепочки, в которой каждое звено содержит ссылку не только на следующее, но и на предшествующее ему звено. Каждое звено начинается со справки стандартного вида из трех значений:

Длина звена

Cсылка на следующее звено

Ссылка на предыдущее звено

В заглавном звене стоит пустая ссылка на предыдущее звено, а в последнем - на следующее звено.

Такие списки позволяют удобным образом перебирать записи не только слева направо, но и справа налево. Поскольку можно двигаться в любую сторону, мы получаем возможность, например, в операции исключения записи указывать саму эту запись, а не предшествующую, как это приходилось делать в случае однонаправленных списков. (Предшествующая запись нам понадобится, но мы найдем ее по соответствующей ссылке в исключающей записи).

Опишем реализацию двунаправленного списка на Паскале.

Пример:

Program Ex37;

uses crt;

Type PDouble = ^Spisok;

Spisok = record

inf: integer;

L, R: PDouble;

end;

var Left, Right, E, NE, Temp: PDouble;

v,i: integer;

begin clrscr;

Read(v); {v-целое число в инф. части 1-го элемента д_списка}

I:=1; writeln(i,'-й эл-т д_списка = ',v);

if v=999 then exit; {999 - признак конца ввода данных}

new(E);

E^.inf:= v;

E^.L:= Nil; E^.R:= Nil;

Left:= E; Right:= E;

while true do

begin

Read(v); inc(i);

writeln(i,'-й эл-т д_списка = ',v);

if v=999 then goto m2; {999 - признак конца ввода данных}

new(E);

E^.inf:= v;

E^.L:= E; E^.R:= Left;

Left:= E;

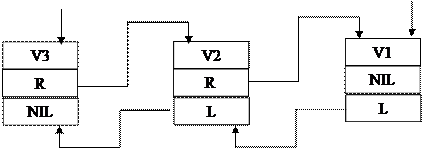end;

end.

Left Right

Рис. 9.7 Организация двухсвязного списка

Добавление нового элемента в список запишем в виде процедуры.

Procedure AddESpisok;

Begin

Read(v); inc(i);

writeln(i,'-й эл-т стека = ',v);

if v=999 then exit; {999 - признак конца ввода данных}

new(NE);

NE^.inf:= v;

NE^.R:= Temp^.R;

NE^.L:= Temp;

Temp^.R^.L:= NE;

Temp^.R:= NE;

End;

Для того чтобы удалить элемент из списка, необходимо указатели соседних элементов переместить друг на друга. Реализуем эти действия в процедуре DelESpisok.

Procedure DelESpisok;

Label m1, m2;

Var b: char;

Begin

m2: Writeln(‘Вв. «Д», если хотите продолжить удаление эл-в’);

Writeln(‘или «Н» в противном случае’);

Read(b);

If (b=’Н’) or (b=’н’) then goto m1 else

If (b=’Д’) or (b=’д’) then

While Right<>Left do

Begin

Temp^.R:= Temp^.R^.R;

Temp^.R^.L:= Temp;

End;

Goto m2;

m1:

End;

Одной из распространенных разновидностей двунаправленных списков являются кольцевые списки. В двунаправленном кольцевом списке последнее звено ссылается как на следующее на заглавное звено, а то в свою очередь - на последнее звено как на предыдущее. Такая организация списка упрощает процедуру поиска или перебора записей с любого места с автоматическим переходом от конца к началу или наоборот.

Включение записи в кольцевой список. Пусть требуется вставить звено с новой записью после звена с индексом i. Новое звено помещается на свободное место и включается в список путем коррекции ссылок в звене с индексом i и в том звене, которое раньше за ним следовало.

Напишем процедуру InRing включения записи в кольцевой список. Запись длины n находится в массиве Inf и вставляется в список после звена, начинающегося с элемента S[i].

Схема процедуры:

1. Заполнить первый элемент справки нового звена (его индекс находится в S[3]) числом n+3;

2. Заполнить второй элемент справки нового звена ссылкой на следующее за вставляемым звено;

3. Заполнить третий элемент справки нового звена ссылкой на предшествующее вставляемому звено;

4. Перенести в массив S запись из массива Inf;

5. Изменить ссылку на предшествующее звено в справке звена, следующего за вставляемым;

6. Изменить ссылку на следующее звено в звене, указываемом значением i;

7. Изменить указатель начала свободного места.

Как и в случае однонаправленного списка, для наглядности используем переменные new и sled.

Procedure InRing (Var S:Spisok; Var Inf:TypeInf; n,i:integer);

Var new, sled, j:integer;

Begin new:=S[3]; sled:=S[i+1];

S[new]:=n+3; S[new+1]:=sled; S[new+2]:=i;

For j:=1 to n do S[new+2+j]:=Inf[j];

S[sled+2]:=new; S[i+1]:=new; S[3]:=S[3]+n+3

End;

Исключение записи из кольцевого списка. Чтобы исключить запись из кольцевого списка, нужно изменить две ссылки: у "соседа слева" поставить ссылку на следующее звено, а у "соседа справа" – ссылку на предыдущее звено.

Как и всякий двунаправленный, кольцевой список имеет то преимущество перед однонаправленным, что можно указать индекс начала исключаемого звена, а не индекс начала звена, предшествующего исключаемому. (Этот последний индекс не обязательно указывать явно, так как его можно найти в справке исключаемого звена).

При описании процедуры OutRing для исключения записи воспользуемся переменными pred=S[i+2] и sled=S[i+1], значениями которых являются соответственно индексы звеньев предшествующего и следующего за исключаемым звеном, которое указывается значением его индекса i.

Procedure OutRing (Var S:spisok;i:integer);

Var sled,pred: integer;

Begin

sled:=S[i+1]; pred:=S[i+2];

S[pred+1]:=sled; S[sled+2]:=pred

End;

9.6.2.3. Иерархические и ассоциативные списки

При объединении информационных записей в список образуется группа записей с определенным внутренним порядком. Можно рассматривать эту группу как единый информационный объект и образовывать списки из таких составных объектов. Например, можно организовать список высших учебных заведений, где каждому ВУЗу соответствует список факультетов. Такая иерархия может быть многоступенчатой, информацию о каждом факультете можно представить как список студентов, информацию о курсе – как список классов, а информацию о классе - как список студентов.

Если элементами списка верхнего уровня являются подчиненные списки, то удобно считать, что с точки зрения списка верхнего уровня входящая в него запись представляет собой ссылки на подчиненный список, оформленные как заголовок этого подчиненного списка (заглавное звено цепочки, представляющей подчиненный список). При этом в теле заголовка подсписка может быть и некоторая смысловая информация общего характера. Например, в заголовке списка cтудентов класса может указываться номер этого класса, фамилия старосты и т.д.

Список верхнего уровня может содержать наряду с заголовками подчиненных списков и самостоятельные элементы (обычные записи).

Таким образом, список верхнего уровня представляется в виде цепочки, в которой каждое звено состоит, во-первых, из справки и, во-вторых, из обычной записи или же заголовка подсписка (списка нижнего уровня иерархии).

Иерархически связанные между собой списки могут быть разных типов.

Часто одни и те же объекты представляют интерес с различных точек зрения, и возникает естественная потребность включать их в различные списки, составляемые по разным признакам. Например, одни и те же члены некоторого коллектива могут входить в разнообразные списки (по возрасту, месту рождения, месту учебы и другим признакам). Если в разных списках нужна одна и та же информация о каждом объекте, то желательно не дублировать записи. Избавиться от такого дублирования позволяют ассоциативные списки. Они организуются на одном общем наборе записей, причем каждый из ассоциативных списков объединяет в определенном порядке те записи из этого набора, которые обладают некоторым характерным признаком

(Слово "ассоциативный" выбрано потому, что мы объединяем записи в список, ассоциируя их по некоторому признаку).

Каждый ассоциативный список представляется в виде отдельной цепочки со своим заглавным звеном, которое помещается на фиксированном месте и позволяет выполнять операции над этим списком автономно. Эти цепочки переплетаются, поскольку одни и те же звенья входят в различные цепочки. Каждое такое звено, как и обычно, состоит из информационной части (записи) и стандартной справки. В справке находится несколько ссылок или пар ссылок (по числу ассоциативных списков, в которые входят эти записи).

9.6.3. Нелинейные структуры данных

Объединение различных списков на базе общего набора записей является информационной сетью.

0иа представляет собой наиболее общую форму организации информации, соответствующую многосвязности объектов в окружающей среде. Элементы данных, описывающие связанные элементы среды, также должны быть связаны между собой (либо через индексную арифметику, либо через сцепление).

Информационная сеть обеспечивает одновременную реализацию различных связей элементов данных с произвольным количеством указателей.

Рис. 9.8 Реализация произвольной информационной сети

Частным случаем сети является дерево.

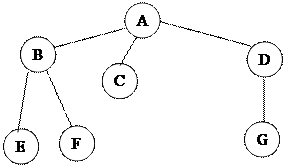
Рис. 9.9 Реализация дерева

Дерево имеет одну корневую вершину (A), на которую не ссылается ни один из элементов дерева, а также листья (E, F, G). Листья – узлы, которые ни на что не ссылаются. Все остальные узлы считаются промежуточными (B, C, D). Если промежуточная вершина ссылается на другие вершины, то ее называют родительской, а те, на которые ссылается она, дочерними. Иногда дочерние вершины называют сыновними.

Дерево может быть представлено в памяти компьютера в виде следующей структуры:

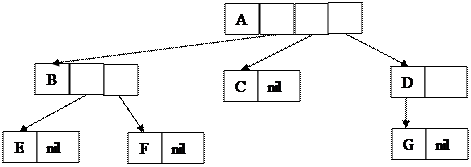Рис. 9.10 Машинное представление дерева

Если каждая вершина дерева ссылается на n дочерних вершин, то дерево называется n – арным деревом. Частным случаем n – арного дерева является бинарное дерево.

Бинарное дерево удобно определять рекурсивно, как дерево содержащее корень и левое бинарное дерево. В простейшем случае бинарное дерево может быть пустым.

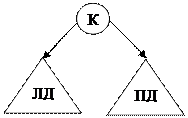В программировании наиболее распространены бинарные и тринарные деревья. На основе этих структур данных строят словари и справочники. В этом случае говорят об упорядоченных деревьях, и порядок задается слева-направо.

Любая вершина в левом поддереве (ЛД) считается меньшей корня, а любая вершина в првом поддереве – большей.

Рис. 9.11 Бинарное дерево

Поскольку бинарное дерево упорядочено, то можно быстро найти любой элемент дерева по схеме бинарного поиска.

Над деревом могут выполняться следуюшие операции:

1) организация дерева;

2) добавление вершины в дерево;

3) удаление вершины из дерева;

4) поиск требуемого элемента в дереве;

5) просмотр дерева.

Просмотр дерева выполняется несколькими способами: сверху-вниз, слева-направо, снизу-вверх.

Любой просмотр разделяется на три элементарные операции:

1) просмотр или обработка корня дерева;

2) просмотр левого поддерева;

3) просмотр правого поддерева.

Если операции выполняются в порядке 1-2-3, то это просмотр сверху-вниз. Если в порядке 2-1-3, то это просмотр слева-направо. Если в порядке 2-3-1, то это просмотр снизу-вверх.

Опишем реализацию бинарного дерева на Паскале.

Пример:

Program Ex38;

uses crt;

Type PTree = ^Tree;

Tree = record

data: integer;

L, R: PTree;

end;

var Up, Ltree, Rtree, Node: PTree;

v: integer;

procedure Grow (var Node: PTree; v: integer);

begin

if Node =nil then

{если текущий узел пустой, то создаем новый узел}

begin

new(Node); Node^.Data:=v;

Node^.L:=nil; Node^.R:=nil;

end else

{если узел не пуст, то вызываем процедуру Grow с соотв. указателем}

if v < Node^.Data then Grow (Node^.L, v)

else if v > Node^.Data then Grow (Node^.R, v)

end;

Begin clrscr;

while true do

Begin

Readln(v); if v=999 then exit;

Grow(Up, v);

End;

end.

Данный пример не обеспечивает получения сбалансированного дерева. Дерево, имеющее n-уровней, называют сбалансированным тогда, когда все n-уровней дерева заполнены и листья могут быть только на n-ом и (n-1)-ом уровнях.

Один из простых алгоритмов получения сбалансированного дерева сводится к следующему:

1) исходный список элементов упорядочивают;

2) берут серединный элемент списка и считают его корнем;

3) в качестве корней левого и правого поддерева берут серединные элементы левого и правого подсписков, и т.д.

Определим операцию добавления элементов в дерево как функцию:

Function AddETree (Up, Node: PTree): Ptree;

Begin

If Up <> nil then

Begin

New (Up); Up^.Data:= Node;

Up^.L:= nil; Up^. R:= nil;

End;

If Up^.Data > Node then Up^.L:= AddETree (Up^.L, Node)

else Up^.R:= AddETree (Up^.R, Node);

AddETree:= Up;

End;

При удалении узла возможны следующие случаи:

1) удаляемый узел не имеет поддеревьев;

2) удаляемый узел имеет лишь одно поддерево;

3) удаляемый узел имеет оба поддерева.

В первом случае достаточно убрать ссылку на удаляемый узел в родительском узле. Во втором случае следует заменить ссылку на удаляемый узел ссылкой на его поддерево. В третьем случае надо заменить удаляемый узел самым левым узлом его правого поддерева.

Вопросы для самоконтроля:

1. Как происходит сегментация оперативной памяти для паскаль-программы? В чем заключается динамическое распределение памяти?

2. Что представляет собой переменная ссылочного типа?

3. Понятие информационной структуры. Виды информационных структур.

4. Как будет выглядеть процедура просмотра и вывода данных из очереди?

5. По какому принципу организуется стек?

6. Что представляет собой и как организуется список? Виды списков.

7. Понятие информационной сети. Особенности бинарных деревьев как подкласса информационных сетей.

ГЛАВА 10

Дата добавления: 2014-12-27