Моделирование взаимосвязей в факторном анализе

Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.

1. Аддитивные модели: y = Σx_i = x₁+x₂+x₃+…+x_{n .}

они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

2. Мультипликативные модели:

Этот тип моделей применяется тогда, когда результирующий показатель представляет собой произведение нескольких факторов.

3. Кратные модели:

Они используются тогда, когда результирующий показатель получают делением одного фактора на величину другого.

Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей:

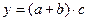и т.д.

Моделирование мультипликативных факторных систем в анализе производственной деятельности предприятия осуществляется путем последовательного расчленения факторов исходной модели на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели:

; ; ,

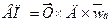где ВП – объем валовой продукции;

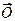- среднесписочная численность рабочих;

Д – количество отработанных дней одним рабочим за год;

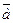- средняя продолжительность рабочего дня, час;

- среднегодовая выработка одного среднесписочного рабочего;

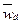- среднедневная выработка одного среднесписочного рабочего;

- среднечасовая выработка одного среднесписочного рабочего.

Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Аналогичным образом осуществляется моделирование аддитивных факторных систем, то есть путем расчленения факторов исходной модели на составные элементы.

Как известно, объем реализации продукции равен:

РП = ВП - Q_нп (2.2.1.)

где РП – объем реализованной продукции;

ВП – валовой объем произведенной продукции;

Q_нп – остатки нереализованной продукции.

Часть нереализованной продукции может находиться на складах предприятия (Q_скл), а часть может быть отгружена потребителям, но еще не оплачена (Q_отг). Тогда исходную модель можно представить:

РП = ВП – Q_скл- Q_отг. (2.2.2)

К классу факторных моделей применяют следующие способы их преобразования: удлинения, расширения и сокращения.

Метод удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в виде функции двух факторов: изменение суммы затрат (Σzq) и объема выпуска продукции (ВП). Исходная модель этой факторной системы будет иметь вид:

. (2.2.3.)

Если общую сумму затрат заменить следующими элементами затрат: оплата труда (ЗП), сырье и материалы (СМ), амортизация (А), накладные расходы (НР) и др., то получим аддитивную модель с новым набором факторов:

, (2.2.4.)

где х₁ – трудоемкость продукции;

х₂ – материалоемкость продукции;

х₃ – фондоемкость продукции;

х₄ – уровень накладных расходов.

Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя исходной модели на один или несколько показателей. Например, если в исходную модель ввести новый показатель с, то модель примет вид:

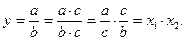(2.2.5.)

В результате получается конечная мультипликативная модель в виде произведения нового набора факторов. Например, среднегодовую выработку продукции одним работником (производительность труда) можно записать таким образом: 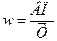(объем валовой продукции делим на среднесписочную численность рабочих). Если введем показатель «количество отработанных дней всеми работниками (Тчел/дни)», то получим следующую модель годовой выработки:

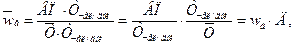(2.2.6.)

где w_д - среднедневная выработка,

Д – количество дней, отработанных одним работником.

Метод сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель. В данном случае получается конечная модель того же типа, что и исходная, но с другим набором факторов. Например, рентабельность совокупных активов предприятия рассчитывается по формуле:

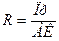, (2.2.7.)

где Пр – сумма прибыли;

АК – среднегодовая стоимость активов.

Если числитель и знаменатель разделим на выручку (стоимость реализованной продукции), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:

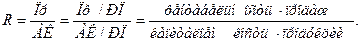(2.2.8.)

Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объема исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя.

Процесс моделирования факторных систем – очень сложный и ответственный момент в анализе производственной деятельности предприятия. От того, насколько реально и точно созданные модели отражают связи между исследуемыми показателями, зависят конечные результаты анализа.

Дата добавления: 2014-12-27