
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Повышения его надежности наиболее ненадежного узла
|
|
|
|
Расчет вероятности безотказной работы системы.
| Элемент | l i | Наработка t, х 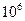 ч ч
| |||||||
х 
| 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 0,95 | 1,425 | |
| 0,05 | 0,9753 | 0,9512 | 0,9277 | 0,9048 | 0,8824 | 0,8607 | 0,9536 | 0,9312 | |
| 2-6 | 0,6065 | 0,3678 | 0,2231 | 0,1353 | 0,082 | 0,0497 | 0,3867 | 0,2405 | |
| 7-10 | 0,5 | 0,7788 | 0,6065 | 0,4723 | 0,3678 | 0,2865 | 0,2231 | 0,6218 | 0,4904 |
| 11-14 | 0,2 | 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,8269 | 0,7520 |
| 0,02 | 0,990 | 0,9801 | 0,9704 | 0,9607 | 0,9512 | 0,9417 | 0,9811 | 0,9719 | |
| 16-17 | - | 0,8451 | 0,6003 | 0,3964 | 0,2519 | 0,1572 | 0,0969 | 0,6238 | 0,4231 |
| - | 0,9510 | 0,8451 | 0,7215 | 0,6003 | 0,4909 | 0,3964 | 0,8569 | 0,7403 | |
| А, C | - | 0,6581 | 0,3640 | 0,1872 | 0,0926 | 0,0450 | 0,0216 | 0,3878 | 0,2074 |
| В | - | 0,5767 | 0,3108 | 0,1609 | 0,0812 | 0,0402 | 0,0197 | 0,3313 | 0,1781 |
| D | - | 0,9505 | 0,7212 | 0,4456 | 0,2434 | 0,1255 | 0,0615 | 0,7494 | 0,4840 |
| E | - | 0,9967 | 0,9794 | 0,9438 | 0,8921 | 0,8282 | 0,7568 | 0,9818 | 0,9503 |
| P | - | 0,9147 | 0,6585 | 0,3786 | 0,1887 | 0,0872 | 0,0377 | 0,6883 | 0,4162 |
13. На рисунке 6 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.

Рисунок 6. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`).
Приложение 2
На основе выполненного количественного анализа узла рассмотрим способ повышения его надежности путем повышения наработки наиболее ненадежного узла.
1. По графику (рисунок 6, кривая P) находим для  (
( ) - процентную наработку системы
) - процентную наработку системы  ч.
ч.
2. Проверочный расчет при  ч показывает (таблица 5), что
ч показывает (таблица 5), что  .
.
3. По условиям задания повышенная  - процентная наработка системы
- процентная наработка системы  ч.
ч.
4. Расчет показывает (таблица 4), что при  ч для элементов преобразованной схемы (рисунок 6)
ч для элементов преобразованной схемы (рисунок 6)  ,
,  ,
, 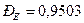 и
и 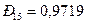 , следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент D и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.
, следовательно, из четырех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент D и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.
5. Для того, чтобы при  ч система в целом имела вероятность безотказной работы
ч система в целом имела вероятность безотказной работы  , необходимо, чтобы элемент D имел вероятность безотказной работы:
, необходимо, чтобы элемент D имел вероятность безотказной работы:
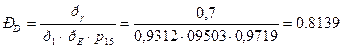 (13)
(13)
При этом значении элемент D останется самым ненадежным в схеме (рисунок 6) и рассуждения в п.4 останутся верными.
Очевидно, значение  , полученное по формуле (13), является минимальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях
, полученное по формуле (13), является минимальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях  увеличение надежности системы будет большим.
увеличение надежности системы будет большим.
6. Чтобы разобраться, почему элемент D имеет самую маленькую вероятность безотказной работы, обратимся к рисунку 5 и таблице 4. Очевидно, что в элементе D самыми «слабыми» являются идентичные элементы A и С. В элементах A и С наименьшие значения вероятности безотказной работы принадлежат элементам 16 и 17. Элемент 16 включает в себя блоки 2 и 3, их значения Р также являются минимальными по отношению к остальным блокам, а элемент 17 включает в себя блоки 5 и 6. Так как блок 4 тоже входит в элемент D и является идентичным с блоками 2-3, 5-6, он тоже будет рассмотрен для определения минимальной необходимой вероятности безотказной работы элемента D.
7. Для определения минимально необходимой вероятности безотказной работы элементов 2-6 необходимо решить уравнение относительно  при
при  . Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графоаналитический метод. Для этого по данным таблицы 5 строим график зависимости
. Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графоаналитический метод. Для этого по данным таблицы 5 строим график зависимости  .
.
График представлен на рисунке 7.

Рисунок 7. Зависимость вероятности безотказной работы системы D от вероятности безотказной работы ее элементов.
8. По графику при  находим
находим  .
.
9. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону формула (10), то для элементов 2-3 при  находим
находим

 (14)
(14)
10. Таким образом, для увеличения  - процентной наработки системы необходимо увеличить надежность элементов 2-3, а следовательно и элементов 5-6 и снизить интенсивность их отказов с
- процентной наработки системы необходимо увеличить надежность элементов 2-3, а следовательно и элементов 5-6 и снизить интенсивность их отказов с  до
до 
 , т.е. в 1,55 раза.
, т.е. в 1,55 раза.
11. Результаты расчетов для системы с увеличенной надежностью элементов 2-6 приведены в таблице 6. Там же приведены расчетные значения вероятности безотказной работы системы D` и системы в целом P`. При  ч вероятность безотказной работы системы, что соответствует условиям задания. График приведен на рисунке 6.
ч вероятность безотказной работы системы, что соответствует условиям задания. График приведен на рисунке 6.
Таблица 6
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 374; Нарушение авторских прав?; Мы поможем в написании вашей работы!