Solution. Find the determinantof

Example 6

Find the determinantof

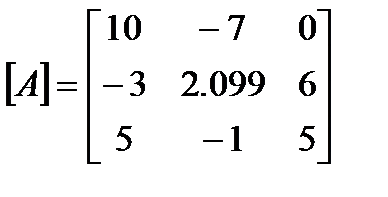
Remember from that at the end of the forward elimination steps of Gaussianelimination with partial pivoting, we obtained

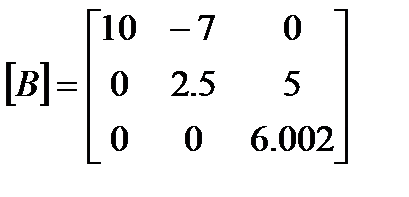
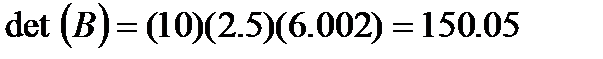
Since rows were switched once during the forward elimination steps of Gaussianelimination with partial pivoting,

.

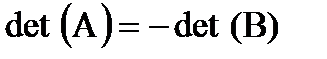
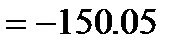Prove det (A) =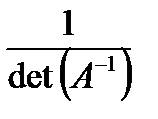

Proof:

[ A ] [ A ]^-1 = [ I ]

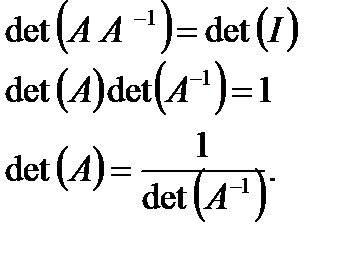
If [ A ] is a n x n matrixand det (A) ¹ 0, what other statements are equivalent to it?

1. [ A ] is invertible.

2. [ A ]^-1 exists.

3. [ A ] [ X ] = [ C ] has a unique solution.

4. [ A ] [ X ] = [0] solution is [ X ] =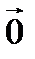

5. [ A ] [ A ]^-1 = [ I ] = [ A ]^-1 [ A ].

Key Terms:

Naïve GaussElimination

Partial Pivoting

Determinant

INTRODUCTION OF MATRIX ALGEBRA
Topic	Gaussian Elimination
Summary	Textbook notes on Gaussian Elimination
Major	All Majors of Engineering
Authors	Autar Kaw
Last Revised	December 26, 2014
Web Site	http://numericalmethods.eng.usf.edu

Дата добавления: 2014-12-27