Преобразование двоичных чисел в десятичную систему счисления. 1 страница

В соответствии с общей формулой позиционных систем счисления двоичное число представимо в виде:

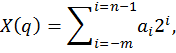
где 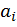могут принимать только два значения 0,1.

Если , то мы имеем представление натурального числа. Соответственно, запись числа 1010 в двоичной системе счисления есть:

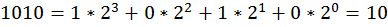
В более общем случае мы работаем с рациональными числами, имеющими целую и дробную части. Как и в десятичной арифметике, дробная часть отделяется от целой точкой или запятой:

.

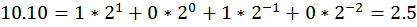Преобразование десятичных чисел в двоичную систему счисления. Решение этой задачи удобно представить не в виде формулы, а в виде алгоритма.

Алгоритм для натуральных десятичных чисел

Этап 1. Поделить заданное десятичное число на два и записать частное и остаток.

Этап 2. Если частное не равно нулю, то выполняем Этап 1 для полученного частного. Если частное равно нулю переходим к Этапу 3.

Этап 3. Двоичное число записывается как последовательность остатков в направлении справа налево.

Алгоритм для дробных десятичных чисел

Этап 1. Умножить заданное десятичное число на два и записать произведение. Если это произведение больше единицы, то записываем в первый разряд двоичного числа единицу, а от полученного произведение отнимаем единицу и записываем «результат». Если произведение меньше единицы, то записываем в разряд двоичного числа ноль, а произведение записывается в «результат» без изменений.

Этап 2. Если результат не равен нулю, то выполняем Этап 1 заменив заданное десятичное число на «результат». Если результат равен нулю переходим к Этапу 3.

Этап 3. Двоичное число записывается как последовательность разрядов в направлении слева направо.

Пример 1. Перевести из Dec в Bin число 42.73

Отдельно переведем целую и дробную части числа. Для перевода целой части (= 42) проводим ряд последовательных делений десятичного числа 42 на 2. При каждом таком делении находим частное (r) и остаток (q). На каждом шаге полученное частное вновь делим на 2 и т.д. Процесс останавливается, когда при очередном делении частное будет равно 0.

42: 2 = 21 (0) r = 21, q = 0

21: 2 = 10 (1) r = 10, q = 1

10: 2 = 5 (0) r = 5, q = 0

5: 2 = 2 (1) r = 2, q = 1

2: 2 = 1 (0) r = 1, q = 0

1: 2 = 0 (1) r = 0, q = 1 (Stop)

Полученные остатки q выписываем, начиная с самого последнего до первого. Это и будет двоичный код числа 42: 101010

Для перевода дробной части 0.73 заданного десятичного числа в Bin проводим ряд последовательных умножений на 2. В полученном произведении на каждом шаге отделяем целую часть (r) от дробной (q). Дробную часть вновь умножаем на 2 и т.д. Процесс заканчивается, если на очередном шаге дробная часть будет равна нулю. Здесь возможны случаи, при которых очередная дробная часть q уже встречалась на предыдущих шагах процесса, то есть мы получим периодическую двоичную дробь. Если такой момент не наступает, мы имеем дело с бесконечной двоичной дробью. Выписываем полученные целые части r в порядке их появления от первой до последней - это и будет искомая двоичная дробь.

0. 73 * 2 = 1. (46) r =1, q= 0.46

0. 46 * 2 = 0. (92) r =0, q= 0.92

0. 92 * 2 = 1. (84) r =1, q= 0.84

0. 84 * 2 = 1. (68) r =1, q= 0.68

0. 68 * 2 = 1. (36) r =1, q= 0.36

и т.д.

Мы прервали перевод дроби 0.73 и получили её приближенное представление в виде дроби системы Bin: 0.10111…

Окончательно получаем: 42.73 в двоичной системе 101010.10111…

Из рассмотренных выше примеров видно, что если десятичное число дробное, то его преобразование в двоичное должно выполняться отдельно над его целой и дробной частями.

Следует иметь в виду, что рассмотренные процедуры перевода целых и дробных чисел из десятичных в двоичные и обратно являются общими для перевода чисел в любых позиционных системах счисления (т.е. целое число делится на основание системы счисления, в которую число переводится, а правильная дробь умножается).

Притом надо помнить, что при выполнении переводов чисел из одной системы счисления в другую все необходимые арифметические действия выполняются в той системе счисления, в которой записано переводимое число.

4. Двоичная арифметика

Правила выполнения арифметических действий над числами в любой системе счисления определяются арифметическими действиями над одноразрядными числами. В десятичной системе счисления мы соответственно имеем десять одноразрядных чисел (от нуля до девяти) и соответствующие таблицы сложения и умножения. В двоичной системе счисления эти таблицы очень просты.

Таблица сложения двоичных чисел:

Таблица умножения двоичных чисел:

Сложение. Как и в десятичной системе счисления, сложение двоичных чисел начинается с правых (младших) разрядов. Если результат сложения цифр обоих слагаемых не помещается в этом же разряде результата, то происходит перенос. Цифра, переносимая в соседний разряд слева, добавляется к его содержимому. Такая операция выполняется над всеми разрядами слагаемых.

Пример.

Сложить два числа в десятичном и двоичном представлении (формат – 1 байт).

Решение:

Перенос (единицы) 11 1111111

Слагаемое 1 099 01100011

Слагаемое 2 095 01011111

Сумма 194 11000010

Операция получается громоздкая со многими переносами, но удобная для ЭВМ.

Вычитание. Операция вычитания двоичных чисел аналогична операции в десятичной системе счисления. Операция вычитания начинается, как и сложение, с младшего разряда. Если содержимое разряда уменьшаемого меньше содержимого одноименного разряда вычитаемого, то происходит заем 1 из соседнего старшего разряда.

Пример.

Вычесть два числа в десятичном и двоичном представлении (формат – 1 байт).

Решение:

Заем (единицы) 1 01100000

Уменьшаемое 109 01101101

Вычитаемое 049 00110001

Разность 060 00111100

Умножение. Как и в десятичной системе счисления, операция перемножения двоичных многоразрядных чисел производится путем образования частичных произведений и последующего их суммирования. Частичные произведения формируются в результате умножения множимого на каждый разряд множителя, начиная с младшего. Каждое частичное произведение смещено относительно предыдущего на один разряд. Поскольку умножение идет в двоичной системе счисления, каждое частичное произведение равно либо 0 (если в соответствующем разряде множителя стоит 0), либо является копией множимого, смещенного на соответствующее число разрядов влево (если в разряде множителя стоит 1). Поэтому умножение двоичных чисел идет путем сдвига и сложения. Таким образом, количество частичных произведений определяется количеством единиц в множителе, а их сдвиг – положением единиц. Положение точки в дробном числе определяется так же, как и при умножении десятичных чисел.

Пример.

Вычислить произведение 17*12=204 в двоичной форме.

Решение:

00010001*00001100=11001100

5.Задачи и решения

Задача 1.Записать в Bin десятичное число 0.15 (в виде двоичной дроби).

Решение:

0.15 * 2 = 0. (3) r = 0, q = 0.3

0.3 * 2 = 0. (6) r = 0, q = 0.6

0.6 * 2 = 1. (2) r = 1, q = 0.2

0.2 * 2 = 0. (4) r = 0, q = 0.4

0.4 * 2 = 0. (8) r = 0, q = 0.8

Задача 2.Десятичное число 0.34375 преобразовать в двоичное число.

Решение:

2 * 0.34375= 0.6875 0

2 * 0.6875= 1.375 1

2 * 0.375 0.75 0

2 * 0.75= 1.5 1

2 * 0.5 =1.0 1

Таким образом, 0.34375(10) = 0.01011(2).

Задача 3. Записать в двоичной системе дроби 3/4, 5/8, 13/16

Решение.

Если знаменатель дроби является степенью двойки, то можно использовать следующий приём для перевода дроби из Dec в Bin.

Покажем, как можно это сделать.

3 = 11(2), 4 = 100(2)  3/4 = 11/100 = 0.11(2);

5 = 101(2), 8 =1000(2) 5/8 = 101/1000 = 0.101(2);

13 = 1101(2), 16 = 10000(2) 13/16 = 1101/10000 = 0.1101(2)

Задача 4. Задано дробное число 3FA.B5 в Hex. Записать это число в Dec.

Решение. Используем запись

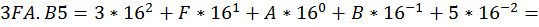
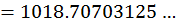
Задача 5. Перевести десятичное число 332 в Hex.

Решение. Как и при переводе из Dec в Bin делим заданное целое на 16 и при каждом таком делении находим частное (r) и остаток (q). Полученное частное вновь делим на 2 и т.д. Если остаток 10< q < 15, то заменяем его на соответствующие буквенные изображения цифр Hex. Затем выписываем остатки по порядку «снизу – вверх»:

332: 16 = 20 (12), 12 это С16

20: 16 = 1 (4)

1: 16 = 0 (1) (Stop)

33210 = 14С16.

6.Вопросы для самопроверки

1.В каких случаях целесообразно применять двоичную и шестнадцатеричную систему счисления?

2.Десятичное число 0.34375 преобразовать в двоичное число.

Ответ: 0.34375(10) = 0.01011(2).

3. Записать в двоичной системе дробь 13/16

Ответ:13/16(10) = 1101/10000 = 0.1101(2)

4. Задано дробное число 3FA.B5 в Hex. Записать это число в Dec.

Ответ: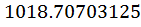

4.Системы представления информации в ЭВМ

Для записи чисел в компьютере используются два основных способа: с фиксированной запятой и с плавающей точкой.

1.Система с фиксированной запятой

Систему представления чисел с фиксированной запятой обозначают как:

P(b, t, f), где b – основание системы счисления, t – количество разрядов для записи числа, f - количество разрядов для записи дробной части.

Рассмотрим пример системы с фиксированной запятой Р(10, 4, 1); здесь b=10, t=4, f=1. Т.е. это десятичная система счисления, общее количество разрядов для записи числа равно 4, под дробную часть отводится 1 знак.

Минимальное число, которое можно записать в этой системе, равно -999.9, максимальное число равно +999.9, всего положительных чисел с нулём 10000, всего отрицательных чисел 9 999.

Любое число из [ -1000; 1000] представимо в системе Р(10, 4, 1) с ошибкой не превышающей 0.05.

Пример.

Пусть задано число x=865.54. Его представление в P(10, 4, 1) обозначим как p(x) = 865.5. Ошибка равна | x - p(x)| = 0.04. Относительная ошибка представления этого числа Е = | x - p(x)| /x = 0.04 / 865.54 =0.000046213, что составляет 0.004%.

Если х = 0.86554, то р(х) = 0.9 (произвели округление при записи числа в системе P(10, 4, 1)), относительная ошибка Е = 0.03446/0.86554 = 0.039813…, что составляет 3.98%.

Таким образом, система P(b, t, f) образует равномерную сетку для представления вещественных чисел, но относительная ошибка при записи вещественных чисел в этой системе не является равномерной.

Система P(b, t, f) используется в современных ЭВМ только для записи целых чисел в двоичной системе (со знаком и без знака), то есть при b = 2, f = 0.

Натуральные числа в ЭВМ. Для кодирования натуральных чисел, как правило, используются поля длиной 1, 2 или 4 байта, т.е. t=8, 16, 32:

Таблица 2.

Название	Длина, байт	Диапазон чисел
byte, unsigned char		0-255
word, unsigned int		0-65 535
unsigned long		0-4 294 967 295

Целые числа со знаком. Для записи целых чисел со знаком, как и в случае натуральных чисел, в современных компьютерах отводиться 8, 16 или 32 бита, т.е. t=8, 16, 32.

Выделенные для записи чисел биты нумеруются справа налево, начиная с нуля. Если целое число со знаком, то старший бит хранит знак числа: 0 соответствует знаку плюс, 1 соответствует знаку минус.

Пример. Целые числа со знаком в системе Р(2, 8, 0). Для их записи отводится 8 бит. Старший (седьмой) бит содержит знак числа: 0 или 1. Вот как будет записано число +75 = 26+23 +21+20 в 8-битовом коде: 0100 1011.

Дополнительный код. Для записи отрицательных целых чисел используется дополнительный код.

Правило для записи отрицательного числа (-N) в дополнительном коде:

1) записать двоичный код соответствующего положительного целого N и дополнить его слева до нужного числа битов нулями (до 8, или до 16, или до 32 битов).

2) инвертировать полученный код (операция инверсии двоичного кода заключается в замене всех 0 на 1 и всех 1 на 0);

3) прибавить к младшему разряду инвертированного кода 1.

Полученный код и будет дополнительным кодом отрицательного числа (-N).

Пример 1. Записать дополнительный 8 битовый код числа -95.

Решение: запишем 95 в двоичном коде:

95 = 64+16+8 +4+2+1 = 101 1111.

Дополним этот код слева нулём (чтобы получилось 8 бит): 0101 1111.

Инвертируем полученный код: 1010 0000.

Прибавим 1 к младшему разряду данного кода: 1010 0001. Это и будет дополнительный двоичный код отрицательного числа -95.

Для проверки сложим полученные коды:

+ 95: 0 1 0 1 1 1 1 1

-95: 1 0 1 0 0 0 0 1

сумма: (1) 0 0 0 0 0 0 0 0

Сумма единиц в 8-ом бите перешла в 9-ый бит, который отсутствует в записи числа – он теряется (говорят, что произошел перенос из знакового бита), и сумма становится равной 0.

Максимальное положительное 8-ми битовое число 0111 1111 = +127.

Восьми битовое число 1000 0001 = -127. Минимальное отрицательное 8-ми битовое равно 1000 0000 = -128. Т.е. диапазон однобайтовых целых чисел со знаком от -128 до +127. Всего с помощью 8-ми бит можно представить 256 чисел.

Для перевода отрицательных чисел из дополнительного кода поступаем также: инвертируем код отрицательного числа, прибавляем 1 к младшему разряду и получаем двоичный код соответствующего положительного числа.

Пример. Какое целое число со знаком записано в 8-ми битовом коде 1010 0011?

Решение: Старший бит равен единице, значит это отрицательное число.

Инвертируем данный код: 0101 1100.

Прибавляем 1 к младшему разряду: 0101 1101.

Переводим число в Dec: 26+24+23+22+20 =64+16+8+4+1 = 93. Т.е. заданный дополнительный код соответствует числу -93.

Для кодирования натуральных чисел, как правило, используются поля длиной 1, 2 или 4 байта, т.е. t=8, 16, 32:

Таблица 3.

Название	Длина, байт	Диапазон чисел
ShortInt		-128.. 127
Integer		-32 768.. 32 767

Для правильной интерпретации содержимого памяти нужно знать, какой тип данных в ней храниться, т.к. по «внешнему виду» отличить один тип от другого нельзя. Пусть, например, 1 байт памяти содержит следующие данные: 1001 1101.

Если это число типа Byte, то оно равно27+24+23+22+20= 128+16+8+4+1=157. Если это целое число со знаком типа ShortInt, то для его определения надо инвертировать код: 0110 0010, затем прибавить 1: получим 0110 0011, т.е. 26+25+21+20= 64+32+2+1 = 99, значит, данный байт содержит число - 99.

2.Числа с плавающей точкой

Такая система используется для записи вещественных чисел в современных ЭВМ.

Пример числа, записанного в виде числа с плавающей точкой:

Здесь 0.31562781 – мантисса числа, 5– его порядок.

Это число в «обычной», позиционной записи выглядит как 31562.781. Такой способ представления чисел позволяет компактно записывать числа из широкого диапазона значений, например:

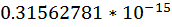
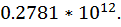
Система представления чисел с плавающей точкой. Систему представления чисел с плавающей запятой обозначают как:

Система F(b, t, L, U). Здесь: b – основание системы (для ЭВМ b всегда равно 2), t - количество разрядов мантиссы, L, U – пределы значений показателя порядка чисел в этой системе.

Числа системы F(b, t, L, U) имеют вид:

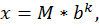
где M – мантисса числа x, b – основание системы счисления, k – порядок числа x.

Развёрнутая запись мантиссы:

Таким образом, компактная запись числа системы F(b, t, L, U):

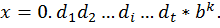
Здесь d1, d2, d3, …. dt - цифры системы счисления; они составляют

мантиссу числа; t – разрядность мантиссы (количество знаков в мантиссе).

Причем, должны выполняться следующие условия:

1) 1<= d1 < b (первая цифра мантиссы не должна равняться нулю);

2) 0 <= di < b, i =2,3,…t;

3) L<=k<= U

Если мантисса удовлетворяет первому условию, то говорят, что число представлено в нормализованном виде (с нормализованной мантиссой). Запись нуля в системе F(b, t, L, U):

Утверждение 1. Система F(b, t, L, U) содержит

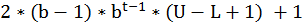
различных чисел.

Утверждение 2. Числа системы F(b, t, L, U) образуют неравномерную сетку, но относительная плотность этой сетки равномерна (всюду одинакова).

Пример 1. Система F(10, 4, -2, 3). Здесь b=10, t=4, L= -2, U=3.

Число x=865.54 в этой системе записывается в виде , а число y=0.86554 имеет вид .

В обоих случаях относительная ошибка 0.005%.

Действительно, | F(x) – x| /x =0.04/865.54 =4/86554; | F(y) –y | /y = 0.00004/0.86554 = 4/86554.

В отличие от системы с фиксированной точкой, здесь относительная ошибка представления чисел одинакова для всех чисел из заданного диапазона.

Пример 2. Системы F(2, 3, -1, 2).

Здесь b=2 (двоичная система), t=3, L= -1, U=2.

Выпишем все положительные числа этой системы.

Сначала заполним столбец числами порядка 20; числа из соседних столбцов получаются умножением (делением) на 2.числа порядка 2-1 числа порядка 20 числа порядка 21 числа порядка 22

0.100 ~ 4/16 0.100 ~ 4/8 0.100 ~ 4/4 0.100 ~ 4/2

0.101 ~ 5/16 0.101 ~ 5/8 0.101 ~ 5/4 0.101 ~ 5/2

0.110 ~ 6/16 0.110 ~ 6/8 0.110 ~ 6/4 0.110 ~ 6/2

0.111 ~ 7/16 0.111 ~ 7/8 0.111 ~ 7/4 0.111 ~ 7/2

Вещественные числа в ЭВМ. В самом общем виде структура представления вещественных чисел в ЭВМ имеет следующий вид:

Знак мантиссы

Знак порядка

Порядок числа

Мантисса

Для хранения знака мантиссы и знака порядка числа отводится по 1 биту; количество бит для хранения порядка и мантиссы зависит от выбранного типа представления данных.

Например, если для хранения дробного числа отведено 32 бита, то их назначение может быть распределено следующим образом (в первой строке стоят номера битов, старший бит под номером 31 - знак числа, мантисса хранится в битах с номерами от 0 до 22, порядок числа в битах с номерами от 23 до 30):

			…				…
Знак числа	Порядок числа	Мантисса

Так как в нормализованной мантиссе двоичного числа в первой позиции всегда стоит единица, то хранят мантиссу, начиная со второго знака. Например, число 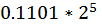хранится как 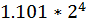, при этом единица целой части числа не хранится. Корректировка происходит при преобразовании числа или в ходе вычислений. При этом порядок дробного двоичного числа при хранении занимает 1 байт и изменяется в диапазоне от -127 до +128, а не от -128 до +127, как было бы в случае нормализованного представления чисел.

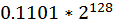Например, если надо записать число , то представляем его как ; число представляется как .

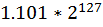Далее, чтобы порядок числа всегда был положительным, к нему прибавляют 127, т.е. если порядок числа -10, то хранится +117. Порядок 100 хранится как 227. Такой способ записи порядка называют смещённым.

Пример 1. Как будет представлено в памяти компьютера число -0.0625, если для его размещения выделено 32 бита памяти?

Решение: 0.0625 = 1/16 = 0.00012, т.е. -0.0625 = -0.1*2-3 = -1.0*2-4; смещенный порядок равен (-4+127) = 123, или в Bin 123 = 11110112; мантисса = 0 (все 23 бита). Старший бит равен 1, т.к. число отрицательное.

Окончательно получаем:

1 0111 1011 000 0000 0000 0000 0000 0000.

Пример 2. Запишите число 25 как число с плавающей запятой, используя 32 бита.

Решение: 25 = 110012 = 1.1001*24. Смещённый порядок равен 4+127 = 131 или 100000112. Мантисса = 1001, окончательно получаем:

0 1000 0011 100 1000 0000 0000 0000 0000.

Стандарт IEEE 754. Стандарт IEEE (Institute of Electrical and Electronics Engineers — Международный институт инженеров по электротехнике и электронике) на представление формата с плавающей точкой в компьютерах был принят в 1985 г. в качестве международного под номером 754. В настоящее время процессоры основных мировых разработчиков (Intel, SPARC, Power и т. д.) придерживаются этого стандарта.

Таблица 4. Диапазоны и точности представления чисел в стандарте IEEE 754

Название	Длина (бит) (порядок, мантисса)	Min	Мах
Real	32 (8, 23)	1,17 · 10-38	3,4 · 10+38
Double	64(11,52)	2,2 · 10-308	1,8 · 10+308
Extended	80(15,64)	3,4 · 10-4932	1,2 · 10+4932

Стандарт IEEE 754 предусматривает, что двоичные коды чисел в формате с плавающей точкой могут занимать поля длиной 4, 8 и 10 байтов. В соответствии с общими принципами кодирования чисел в этом формате поля содержат код знака числа, код порядка, а также код мантиссы.

3.Система кодирования символов.

В настоящее время международным стандартом стала двухбайтовая система кодирования символов Unicode, разработанная Unicode Consortium. Unicode Consortium является некоммерческой организацией, основанной для разработки и развития стандарта Unicode, определяющего представление символьной информации в современных программных продуктах, и для содействия его широкому распространению и использованию.

Система Unicode присваивает уникальный двухбайтовый код любому символу, независимо от платформы, независимо от программы, независимо от языка.

Следует отметить, что для сохранения преемственности программного обеспечения Unicode включает в себя как подмножества прежние наиболее распространенные однобайтовые системы кодирования символов.

4.Вопросы для самопроверки

1. Преобразуйте каждое представленное ниже значение в двоичном дополнительном коде в десятичный формат:

а) 00011; б) 01111; в) 11100; г) 11010; д) 00000; е) 10000.

Решения: а) 3; б) 15; в) –4; г) –6; д) 0; е) –16.

2. Преобразуйте каждое представленное ниже десятичное значение в двоичный дополнительный код длиной восемь бит:

а) 6; б) 26; в) 217; г) 13; д) 21; е) 0.

Решения: а) 00000110; б) 11111010; в) 11101111; г) 00001101; д) 11111111; е) 0000000.

3. Предположим, что приведенные ниже комбинации битов представляют числа в двоичном дополнительном коде. Запишите представление обратных им значений в этом же коде: а) 00000001; б) 01010101; в) 11111100; г) 11111110; д) 00000000; е) 01111111.

Решения: а) 11111111; б) 10101011; в) 00000100; г) 00000010; д) 00000000; е) 10000001.

4. Предположим, что числа в машине сохраняются в двоичном дополнительном коде. Какое наибольшее и наименьшее число может быть записано, если используются битовые комбинации следующей длины:

а) четыре; б) шесть; в) восемь.

Решения:

а) При 4 битах наибольшее число равно 7, а наименьшее – –8.

б) При 6 битах наибольшее число равно 31, а наименьшее – –32.

в) При 8 битах наибольшее число равно 127, а наименьшее – 128.

5. Алгебраические основы ЭВМ

Математическая теория цифровых вычислительных машин во многом базируется на методах и подходах развитых в современной алгебре. Основополагающими здесь могут считаться алгебра Буля, машина Тьюринга и, наконец, модель компьютера, предложенная и реализованная фон Нейманом.

1.Основные законы арифметики

Действия и преобразования, применяемые в обычной алгебре, в которой буквами обозначаются числа, основываются на небольшом числе определений и формул.

I. Существует арифметическое действие, называемое сложением и обозначаемое знаком «+».

Принимается, что для каждой пары двух чисел 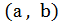существует единственное определенное число «с», называемое суммой чисел (а, b).

Действие сложения обладает переместительным и сочетательным свойствами.

Отсюда формулы:

1) (существование единственной суммы чисел а, b),

2) (переместительное свойство, коммутативность операции сложения),

3) (сочетательное свойство, ассоциативность операции сложения).

II. Существует второе арифметическое действие, называемое умножением и обозначаемое знаком «*» (этот знак при употреблении буквенных обозначений обычно опускается).

Действие умножения обладает теми же свойствами, что и сложение: для каждых двух чисел а и b существует определенное единственное произведение с, и действие умножения обладает переместительным и сочетательным свойствами, которые дают формулы:

4) 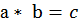(существование единственного произведения чисел а, b),

5) 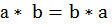(переместительное свойство, коммутативность операции произведения),

6) (сочетательное свойство, ассоциативность операции произведения).

Сложение и умножение обладают распределительным свойством: чтобы умножить сумму двух слагаемых на третье число, можно умножить каждое слагаемое отдельно на это число и полученные произведения сложить:

7) (распределительное свойство, дистрибутивность).

Дата добавления: 2014-12-27