Системы счисления

СИСТЕМЫ СЧИСЛЕНИЯ МИКРОЭВМ. ДВОИЧНАЯ АРИФМЕТИКА. РАЗРЯДНЫЕ СЕТКИ. ПРЯМОЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ

Система счисления - это способ представления любого числа посредством некоторого алфавита символов. Различают непозиционные системы счисления (например, римская), позиционные (десятичная, двоичная, восьмеричная, шестнадцатеричная и др.) и системы с иррациональным основанием (коды Фибоначчи). Количество раз­личных цифр в позиционной системе называют основанием системы S.

Любое число N в позиционной системе с основанием S пред­ставляется формулой

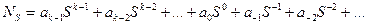, (2.1)

где k - количество цифр в числе N; a - любые из S цифр системы счисления.

Если найдено представление числа N в виде (2.1), то само число можно записать в виде:

(2.2)

Например, если десятичное число выражается полиномом 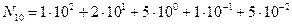, то само число равно 125,15₁₀.

В двоичной системе счисления (2 с/с) используются только две цифры: 0 и 1; в восьмеричной (8 с/с) - восемь цифр: 0-7; в шест­надцатеричной (16 с/с) - десять цифр: 0-9 и шесть букв: А, В, С, D, Е, F. МикроЭВМ так же, как и другие ЭВМ, работают с инфор­мацией, представленной в 2 с/с.

Для связи оператора с микроЭВМ (для ввода и вывода данных, команд, адресов) используется 8 с/с (микроЭВМ типа DEC) или 16 с/с (микроЭВМ типа INTEL), так как в 2 с/с запись информа­ции получается длинной и неудобной для оператора.

Перевод чисел из 10 с/с в другую позиционную систему с основанием S осуществляется по разным правилам для целой и дробной частей числа.

Перевод целых чисел. Для перевода целого числа из 10 с/с в систему с основанием (2 с/с, 8 с/с, 16 с/с) необходимо последовательно разделить это число и получаемые частные на основание S до тех пор, пока час­тное не станет меньше S. Запись числа производится, начиная с последнего частного, с присоединением остатков в последовательно­сти, обратной их получению.

Пример. Перевести число 33₁₀ в 2 с/с.

-
	-
			-
					-
							-

Запись. 33₁₀ = 100001₂ = 41₈ =21₁₆.

Перевод дробных чисел. Для перевода дробной части из 10 с/с в систему S (2 с/с, 8 с/с, 16 с/с) необходимо умножить эту дробь и дробные части (без учета целых) получающихся произведений на основание S. Запись дроби производится с нуля с добавлением после запятой целых частей (сверху - вниз) получающихся произведений. Если при последовательном умножении после запятой не получаются нули, то перевод осуществляется с заданной точностью.

Пример. Перевести 0,625₁₀ в 2 с/с.

X	0,
X	1,
X	0,
	1,

Запись: 0,625₁₀ = 0,101₂ = 0,5₈ = 0,A₁₆.

В последней записи число 10 заменено символом А в соответствии со способом кодирования в 16 с/с (см. табл.2.1).

Перевод чисел из 10 с/с в 2 с/с можно производить, используя формулу (2.1), а также через 8 с/с или 16 с/с.

Очевидно, что основания 8 с/с и 16 с/с есть степени основания 2 с/с: 2³ = 8, а 2⁴ = 16. Следовательно, для записи каждой цифры восьмеричного числа необходимо три двоичных разряда (триада), а для представления каждой цифры шестнадцатеричного числа – четыре разряда (тетрада). Представление десятичных, восьмеричных и шестнадцатеричных целых чисел приведено в табл.2.1.

Перевод двоичных чисел в 8 с/с и 16 с/с. Производится путем разбиения двоичного числа на триады и тетрады соответственно влево и вправо от запятой с последующей заменой триад и тетрад на их символьные эквиваленты в соответст­вии с табл.2.1. Недостающие позиции в триадах и тетрадах запол­няются нулями.

Таблица 2.1. Представление чисел.

10 c/c	2 c/c	8 c/c	16 c/c
			A
			B
			C
			D
			E
			F

Перевод чисел из 8 с/с и 16 с/с в двоичную. Производится заменой каждой цифры соответствующего числа двоичной триадой и двоичной тетрадой согласно таблице 2.1. Для дробных чисел можно написать аналогичную таблицу.

Пример. Перевести 10001,0­­1₂­ в 8 с/c и 16 с/c.

Запись: 010 001,010₂ = 21,2₈

0001 0001,0100₂ = 11,4₁₆

Дата добавления: 2014-12-23