Недетерминированные конечные автоматы

Конечные автоматы

Распознавателем языка называется программа, которая получает на входе строку x и отвечает «да», если x – предложение языка, или в противном случае «нет». Регулярное выражение компилируется в распознаватель путем построения обобщенной диаграммы переходов, называемой конечным автоматом. Такой автомат может быть детерминированным или недетерминированным (недетерминированный автомат может иметь более одного перехода из состояния при одном и том же входном символе).

Как детерминированные, так и недетерминированные конечные автоматы способны к распознаванию точных регулярных множеств. Таким образом, они могут распознавать все, что могут обозначать регулярные выражения. Однако детерминированные конечные автоматы, которые приводят к более быстрому распознаванию, обычно больше по размеру, чем эквивалентные недетерминированные. Существуют методы преобразования регулярных выражений в оба типа конечных автоматов.

Недетерминированный конечный автомат A=(Q, V, δ, q_0, F) представляет собой математическую модель, состоящую из

· множества состояний Q;

· множества входных символов V (символов входного алфавита);

· функции переходов δ, которая отображает пары символ-состояние на множество состояний;

· состояния q₀, известного как стартовое (начальное);

· множества состояний F, известных как допускающие (конечные);

НКА может использоваться в виде помеченного ориентированного графа, так называемого графа переходов, узлы которого представляют собой состояния, а помеченные дуги составляют функцию переходов. Такой граф похож на диаграмму переходов, однако один и тот же символ может помечать два и более переходов из одного состояния, а некоторые переходы могут быть помечены специальным символом e, как обычным входным символом (e-переходы).

Граф переходов для НКА, распознающего язык (a|b)*abb, показан на рисунке 12. Множество состояний НКА – {0, 1, 2, 3}, а входной алфавит – { a, b }. Состояние 0 стартовое, а заключительное 3 представлено двойным кружком.

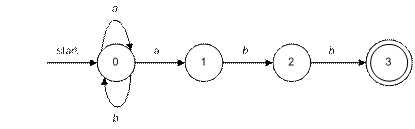
Рис. 12. Недетермированный конечный автомат

Функция переходов НКА может быть реализована различными способами. Простейший из них — таблица переходов, в которой строки представляют состояния, а столбцы — входные символы. Запись в строке i для символа а является множест­вом состояний, которые могут быть достигнуты переходом из состояния i при входном символе а. Таблица переходов для НКА показана на рис. 13.

Состояние	Входной символ
	а	b
	{0,1}	{0}
	-	{2}
	-	{3}

Рис. 13. Таблица переходов для конечного автомата на рис. 12

Представление автомата таблицей переходов обеспечивает быстрый доступ к переходам из данного состояния по данному символу. Вместе с тем таблица за­нимает слишком много места, когда входной алфавит велик и большинство переходов ведут в пустое множество состояний.

НКА допускает, или принимает входную строку х (а эта строка является допустимой), когда в графе переходов существует некоторый путь от начального состояния к какому-либо из заключительных, такой, что метки дуг этого пути соответствуют строке х. НКА на рис. 12 допускает входные строки abb, aabb, babb, aaabb,.... Например, aabb допускается по пути из 0 вдоль дуги а в состояние 0, затем в состояния 1, 2 и 3 вдоль дуг, помеченных соответственно а, b и b.

Путь может быть представлен в виде последовательности переходов состояний, так называемых перемещений. Следующая диаграмма показывает пере­мещения, выполненные для входной строкиaabb:

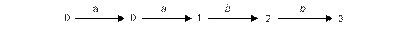
Вообще говоря, в заключительное состояние может приводить более чем одна после­довательность перемещений. Входная строка aabb может быть получена и другими последовательностями перемещений, которые не приводят в заключи­тельное состояние. Например, для той же входной строки aabb может быть выполнена следующая последовательность перемещений, оставляющая нас в состоянии 0.

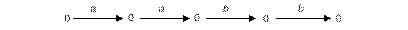
Язык, определяемый НКА, представляет собой множество допускаемых им выходных строк. НКА на рис. 12 допускает строки (a|b)*abb.

Дата добавления: 2014-12-27