Цепочки вывода. Сентенциальная форма. Вывод. Цепочки вывода

Примеры классификации языков и грамматик

Классификация языков

Классификация грамматик по Хомскому

Классификация языков и грамматик

Выше уже упоминались различные типы грамматик, но не было указано, как и по какому принципу они подразделяются на типы. Для человека языки бывают простые и сложные, но это сугубо субъективное мнение, которое зачастую зависит от личности человека.

Для компиляторов языки также можно разделить на простые и сложные, но в данном случае существуют жесткие критерии для этого разделения. От того, к какому типу относится тот или иной язык программирования, зависит сложность распознавателя для этого языка. Чем сложнее язык, тем выше вычислительные затраты компилятора на анализ цепочек исходной программы, написанной на этом языке, а следовательно, сложнее сам компилятор и его структура. Для некоторых типов языков в принципе невозможно построить компилятор, который бы анализировал исходные тексты на этих языках за приемлемое время на основе ограниченных вычислительных ресурсов (именно по этому до сих пор невозможно создавать программы на естественных языках, например на русском или на английском).

Формальные грамматики классифицируются по структуре их правил. Если все без исключения правила грамматики удовлетворяют некоторой заданной структуре, то ее относят к определенному типу. Достаточно иметь в грамматике одно правило, не удовлетворяющее требованию структуры правил, и она уже не попадает в заданный тип.

По классификации Хомского выделяют четыре типа грамматик.

Тип 0: грамматики с фразовой структурой

На структуру их правил не накладывается никаких ограничений: для грамматики вида G(T,N,P,S), V= NÈT правила имеют вид:a®b, где aÎV⁺,bÎV*.

Это самый общий тип грамматик. В него попадают все без исключения формальные грамматики, но часть из них может быть также отнесена и к другим классификационным типам. Грамматики, которые относятся только к типу 0 и не могут быть отнесены к другим типам, являются самыми сложными по структуре.

Практического применения грамматики, относящиеся только к типу 0, не имеют.

Тип 1: контекстно-зависимые (КЗ) и неукорачивающие грамматики

В этот тип входят два основных класса грамматик.

Контекстно-зависимые грамматики G(T,N,P,S),V=NÈT имеют правила вида: a₁Aa₂®a₁ba₂, где a₁, a₂ÎV*,AÎN,bÎV⁺.

Структура правил КЗ - грамматик такова, что при построении предложений заданного ими языка один и тот же нетерминальный символ может быть заменен на ту или иную цепочку символов в зависимости от того контекста, в котором он встречается. Именно поэтому эти грамматики называются «контекстно-зависимыми». Цепочки a₁ и a₂ в правилах грамматики обозначают контекст (a - левый контекст, а a₂ - правый контекст), в общем случае любая из них (или даже обе) может быть пустой. Значение одного и того же символа может быть различным в зависимости от того, в каком контексте он встречается.

Неукорачивающие грамматики G(T,N,P,S), V=NÈT имеют правила вида: a®b, где a,bÎV⁺,| b| ≥|a|.

Неукорачивающие грамматики имеют такую структуру правил, что при построении предложений языка, заданного грамматикой, любая цепочка символов может быть заменена на цепочку символов не меньшей длины. Отсюда и название «неукорачивающие».

Доказано, что эти два класса грамматик эквивалентны. Это значит, что для любого языка, заданного контекстно-зависимой грамматикой, можно построить неукорачивающую грамматику, которая будет задавать эквивалентный язык, и наоборот: для любого языка, заданного неукорачивающей грамматикой, можно построить контекстно-зависимую грамматику, которая будет задавать эквивалентный язык.

При построении компиляторов такие грамматики не применяются, поскольку языки программирования, рассматриваемые компиляторами, имеют более простую структуру и могут быть построены с помощью грамматик других типов.

Тип 2: контекстно-свободные (КС) грамматики

Контекстно-свободные (КС) грамматики G(T,N,P,S); V=NÈT имеют правила вида: A®b, где AÎN, bÎV⁺. Такие грамматики также иногда называют неукорачивающими контекстно-свободными (НКС) грамматиками (потому, что в правой части правил у них должен всегда стоять как минимум один символ).

Существует также почти эквивалентный им класс грамматик – укорачивающие контекстно-свободные (УКС) грамматики G(T,N,P,S), V=NÈT, правила которых могут иметь вид: A®b, где A Î VN, bÎV*.

Разница между этими двумя классами грамматик заключается лишь в том, что в УКС -грамматиках в правой части правил может присутствовать пустая цепочка (l), а в НКС -грамматиках – нет. Язык, заданный НКС - грамматикой, не может содержать пустой цепочки. Доказано, что эти два класса грамматик почти эквивалентны. В дальнейшем, говоря о КС-грамматиках, не будет уточняться, какой класс грамматик (УКС или НКС) имеется в виду, если возможность наличия в языке пустой цепочке не имеет принципиального значения.

КС-грамматики широко используются при описании синтаксических конструкций языков программирования. Синтаксис большинства известных языков программирования основан именно на КС-грамматиках.

Тип 3: регулярные грамматики

К типу регулярных относятся два эквивалентных класса грамматик: леволинейные и праволинейные.

Леволинейные грамматики G(T,N,P,S), V=NÈT могут иметь правила двух видов: A®Bg или A®g, где A, BÎN, gÎVT*.

Праволинейные грамматики G(T,N,P,S), V=NÈT могут иметь правила тоже двух видов:A®gB или A®g, где A, BÎN, gÎ VT*.

Эти два класса грамматик эквивалентны и относятся к типу регулярных грамматик.

Регулярные грамматики используются при описании простейших конструкций языков программирования: идентификаторов, констант, строк, комментариев и т.д. Эти грамматики исключительно просты и удобны в использовании, поэтому в компиляторах на их основе строятся функции лексического анализа входного языка.

Типы грамматик относятся между собой особым образом. Из определения типов 2 и 3 видно, что любая регулярная грамматика является КС-грамматикой, но не наоборот. Также очевидно, что любая грамматика может быть отнесена и к типу 0, поскольку он не накладывает никаких ограничений на правила. В то же время существуют укорачивающие КС-грамматики (тип 2), которые не являются ни контекстно-зависимыми, ни неукорачивающими (тип 1), поскольку могут содержать правила вида «А→l», недопустимые в типе 1. В целом сложность грамматики обратно пропорциональна тому максимально возможному номеру типа, к которому может быть отнесена грамматика. Грамматики, которые относятся только к типу 0, являются самыми сложными, а грамматики, которые можно отнести к типу 3 – самыми простыми.

Языки классифицируются в соответствии с типами грамматик, с помощью которых они заданы. Причем, поскольку один и тот же язык в общем случае может быть задан сколь угодно большим количеством грамматик, которые могут относиться к различным классификационным типам, то для классификации самого языка среди всех его грамматик всегда выбирается грамматика с максимально возможным классификационным типом. Например, если язык L может быть задан грамматиками G1 и G2, относящимся к типу 1 (контекстно - зависимые), грамматикой G3, относящийся к типу 2 (контекстно-свободный), и грамматикой G4, относящийся к типу 3 (регулярные), то сам язык должен быть отнесен к типу 3 и является регулярным языком.

От классификационного типа языка зависит не только то, с помощью какой грамматики можно построить предложения этого языка, но и то, насколько сложно распознать эти предложения. Распознать предложения – значит построить распознаватель для языка. Сложность распознавателя языка напрямую зависит от классификационного типа, которому относится язык.

Сложность языка убывает с возрастанием номера классификационного типа языка. Самыми сложными являются языки типа 0, самыми простыми – языки типа 3. Согласно классификации грамматик, существуют так же 4 типа языков.

Тип 0: языки с фразовой структурой

Это самые сложные языки, которые могут быть заданы только грамматикой, относящейся к типу 0. Для распознавания цепочек таких языков требуются вычислители, равномощные машине Тьюринга. Поэтому можно сказать, что если язык относится к типу 0, то для него невозможно построить компилятор, который гарантированно выполнял бы разбор предложений языка за ограниченное время на основе ограниченных вычислительных ресурсов.

Практически все естественные языки общения между людьми, строго говоря, относятся именно к этому типу языков. Дело в том, что структура и значение фразы естественного языка может зависеть не только от контекста данной фразы, но и от содержания того текста, где эта фраза встречается. Одно и то же слово в естественном языке может не только иметь разный смысл в зависимости от контекста, но и играть различную роль в предложении. Именно поэтому столь велики сложности в автоматизации перевода текстов, написанных на естественных языках, а также отсутствуют компиляторы, которые бы воспринимали программы на основе таких языков.

Тип 1: контекстно-зависимые (КЗ) языки

Тип 1- второй по сложности тип языков. В общем случае время на распознавание предложений языка, относящегося к типу 1, экспоненциально зависит от длины исходной цепочки символов.

Языки и грамматики, относящиеся к типу 1, применяются в анализе и переводе текстов на естественных языках. Распознаватели, построенные на их основе, позволяют анализировать тексты с учетом контекстной зависимости в предложениях входного языка (но они не учитывают содержание текста, поэтому в общем случае для точного перевода с естественного языка все же требуется вмешательство человека). На основе таких грамматик может выполняться автоматизированный перевод с одного естественного языка на другой, ими могут пользоваться сервисные функции проверки орфографии и правописания в языковых процессорах.

В компиляторах КЗ - языки не используются, поскольку языки программирования имеют более простую структуру.

Тип 2: контекстно-свободные (КС) языки

КС-языки лежат в основе синтаксических конструкций большинства современных языков программирования, на их основе функционируют некоторые довольно сложные командные процессоры, допускающие управляющие команды цикла и условия. Эти обстоятельства определяют распространенность данного класса языков.

В общем случае время на распознавание предложений языка, относящегося к типу 1, полиноминально зависит от длины исходной цепочки символов (в зависимости от класса языка это либо кубическая, либо квадратичная зависимость). Однако среди КС-языков существует много классов языков, для которых эта зависимость линейна. Многие языки программирования можно отнести к одному из таких классов.

Тип 3: регулярные языки

Регулярные языки – самый простой тип языков. Время на распознавание предложений регулярного языка линейно зависит от длины исходной цепочки символов.

Регулярные языки лежат в основе простейших конструкций языков программирования (идентификаторов, констант и т.д.), кроме того, на их основе строятся многие мнемокоды машинных команд (языки ассемблеров), а также командные процессоры, символьные управляющие команды и другие подобные структуры.

Регулярные языки – очень удобное средство. Для работы с ними можно использовать регулярные множества и выражения, конечные автоматы [1].

На рис. 19 приведена иерархия языков и соответствующие ей иерархии грамматик и автоматов как распознающих устройств.

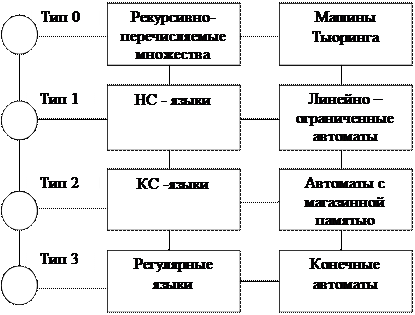Рис. 19. Иерархия языков, грамматик и автоматов

Классификация языков идет от простого к сложному. Если мы имеем регулярный язык, то можно утверждать, что он также является и контекстно-свободным, и контекстно-зависимым, и даже языком с фразовой структурой. В то же время известно, что существуют КС-языки, которые не являются регулярными, ни контекстно-свободными.

Примеры некоторых языков указанных типов.

Грамматика для целых десятичных чисел со знаком

G({0,1,2,3,4,5,6,7,8,9,-,+},{S,T,F},P,S):

P:

S®T +T |-T

T®F | TF

F® 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

По структуре своих правил данная грамматика G относится к контекстно-свободным грамматикам (тип 2). Ее можно отнести и к типу 0, и к типу 1, но максимально возможным является именно тип 2. К типу 3 эту грамматику отнести нельзя, т.к. строка T→F│TF содержит правило T→TF, которое недопустимо для типа 3, и, хотя все остальные правила этому типу соответствует, одного несоответствия достаточно.

Для того же самого языка (целых десятичных чисел со знаком) можно построить и другую грамматику G’({0,1,2,3,4,5,6,7,8,9,-,+},{S,T},P,S):

P:

S®T |+T |-T

T®0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0T | 1T | 2T | 3T | 4T | 5T | 6T | 7T | 8T | 9T

По структуре своих правил грамматика G’является праволинейной и может быть отнесена к регулярным грамматикам (тип3).

Для этого же языка можно построить эквивалентную леволинейную грамматику (тип3) G”({0,1,2,3,4,5,6,7,8,9,-,+},{S,T},P,S):

P:

T®+|-|l

S® T0 | T1| T2 | T3| 4 | T5 | T6 | T7 | T8 | T9 | S0 | S1 | S2 | S3 | S4 | S5 | S6 |S7 | S8 | S9

Следовательно, язык целых десятичных чисел со знаком, заданный грамматиками G,G’и G”, относится к регулярным языкам (тип3).

Для произвольного языка, заданного некоторой грамматикой, в общем случае довольно сложно определить его тип. Не всегда можно построить грамматику максимально возможного типа для произвольного языка. К тому же при строгом определении типа требуется еще доказать, что две грамматики (первоначально имеющаяся и вновь построенная) эквивалентны, а также то, что не существует для того же языка грамматики с большим по номеру типом. Это нетривиальная задача, которую не так легко решить.

Вывод - это процесс порождения предложения языка на основе правил определяющих язык грамматики.

Цепочка b=d₁gd₂ называется непосредственно выводимой из цепочки a=d₁ωd₂ в грамматике G(T,N,P,S), V=TÈN, d₁,g,d₂ÎV*,ωÎV⁺, если в грамматике G существует правило:ω®g Î P. Непосредственная выводимость цепочки b из цепочки a обозначается так:aÞb. То есть, цепочка b выводима из цепочки a, если можно взять несколько символов в цепочке a, заменить их на другие символы по некоторому правилу грамматики и получить цепочку b. В формальном определении непосредственной выводимости любая из цепочек d₁ или d₂ (или обе эти цепочки) может быть пустой. В предельном случае вся цепочка a может быть заменена на цепочку b, тогда в грамматике G должно существовать правило: a®bÎP.

Цепочка b называется выводимой из цепочки a (обозначается aÞ*b) в том случае, если выполняется одно из двух условий:

● b непосредственно выводима из a (aÞb);

● $ g, такая, что: g выводима из a и b непосредственно выводима из g (aÞ*g и gÞb).

Это рекурсивное определение выводимости цепочки. Суть его заключается в том, что цепочка b выводима из цепочки a, если aÞb или же если можно построить последовательность непосредственно выводимых цепочек от a к b следующего вида: aÞg₁Þ…Þg_iÞ…Þg_nÞb, n ³ 1. В этой последовательности каждая последующая цепочка g_i непосредственно выводима из предыдущей цепочки g_i-1.

Такая последовательность непосредственно выводимых цепочек называется выводом или цепочкой вывода. Каждый переход от одной непосредственно выводимой цепочки к следующей в цепочке вывода называется шагом вывода. Очевидно, что шагов вывода в цепочке вывода всегда на один больше, чем промежуточных цепочек. Если цепочка b непосредственно выводима из цепочки a: aÞb, то имеется всего один шаг вывода.

Пример грамматики для целых десятичных чисел со знаком

G ({0,1,2,3,4,5,6,7,8,9,-,+},{S,T,F},P,S):

P:

S®T | +T | -T

T®F | TF

F®0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |9

Построим в ней несколько произвольных цепочек вывода:

1. SÞ-TÞ-TFÞ-TFFÞ-FFFÞ-4FFÞ-47FÞ-479

2. SÞTÞTFÞT8ÞF8Þ18

3. TÞTFÞT0ÞTF0ÞT50ÞF50Þ350

Получили следующие выводы:

1. SÞ*-479 или SÞ+-479 или SÞ7479

2. SÞ* 18 или SÞ+18 или SÞ518

3. TÞ* 350 или T Þ+350 или TÞ6350

Все эти выводы построены на основе грамматики G. В принципе в этой грамматике можно построить сколь угодно много цепочек вывода.

Дата добавления: 2014-12-27