Дерево вывода. Методы построения дерева вывода

Левосторонний и правосторонний выводы

Сентенциальная форма грамматики. Язык, заданный грамматикой

Вывод называется законченным, если на основе цепочки b, полученной в результате вывода, нельзя больше сделать ни одного шага вывода. Иначе говоря, вывод называется законченным, если цепочка b, полученная в результате вывода, пустая или содержит только терминальные символы грамматики G(T,N,P,S):

bÎT*. Цепочка b, полученная в результате законченного вывода, называется конечной цепочкой вывода.

В рассмотренном выше примере все построенные выводы являются законченными, а, например, вывод SÞ*-4FF(из первой цепочки в примере) будет незаконченным.

Сентенциальная форма грамматики G(T,N,P,S), V=TÈN – это цепочка символов aÎV* выводимая из стартового символа грамматики S:

SÞ*a. Если цепочка aÎT* получена в результате законченного вывода, то она называется конечной сентенциальной формой или предложением языка, порождаемого данной грамматикой.

В рассмотренном выше примере цепочки символов «-479» и «18» являются конечными сентенциальными формами грамматики целых десятичных чисел со знаком, так как существуют выводы SÞ*-479 и SÞ* 18 (примеры 1 и 2). Цепочка F8 из вывода 2 является сентенциальной формой, поскольку справедливо SÞ* F8, но она не является конечной цепочкой вывода.

Язык L, заданный грамматикой G(T,N,P,S) - это множество всех конечных сентенциальных форм грамматики G. Язык L, заданный грамматикой G, обозначается как L(G). Очевидно, что алфавитом такого языка L(G) будет множество терминальных символов грамматики T, поскольку все конечные сентенциальные формы грамматики - это цепочки над алфавитом T.

Две грамматики G(T,N,P,S) и G’(T’,N’,P’,S’) называются эквивалентными, если эквивалентны заданные ими языки: L(G)=L(G’). Эквивалентные грамматики должны иметь пересекающиеся множества терминальных символов VTÇVT’¹ Æ (как правило, эти множества совпадают VT=VT’), а вот множества нетерминальных символов, правила грамматики и стартовый символ у них могут кардинально отличаться.

Левосторонний вывод – вывод, в котором на каждом шаге правило грамматики применяется всегда к крайнему левому нетерминальному символу в цепочке.

Правосторонний вывод – вывод, в котором на каждом шаге правило грамматики применяется всегда к крайнему правому нетерминальному символу в цепочке.

В цепочках вывода из того же примера, вывод 1 является левосторонним, выводы 2,3 – правосторонними.

Для грамматик типов 2 и 3 (КС-грамматик и регулярных грамматик) для любой сентенциальной формы всегда можно построить левосторонний и правосторонний выводы. Для грамматик других типов это не всегда возможно, так как по структуре их правил не всегда можно выполнить замену крайнего левого или крайнего правого нетерминального символа в цепочке.

Деревом вывода грамматики G=(T,N,P,S) называется дерево (граф), которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:

· каждая вершина дерева обозначается символом грамматики А Î(TÈN);

· корнем дерева является вершина, обозначенная стартовым символом грамматики – S;

· листьями дерева являются вершины, обозначенные терминальными символами грамматики или символом пустой цепочки λ;

· если некоторый узел дерева обозначен символом AÎN, а связанные с ним узлы – символами b₁b₂,…,b_n; n>0, " n ≥ i > 0; b_i (TÈNÈ{λ}), то в грамматике G=(T,N,P,S) существует правило A→b₁,b₂,…b_nÎP.

Из определения видно, что по структуре правил дерево вывода в указанном виде всегда можно построить только для грамматик типов 2 и 3 (контекстно-свободных и регулярных). Для грамматик других типов дерево вывода в таком виде можно построить не всегда (либо же оно будет иметь несколько иной вид).

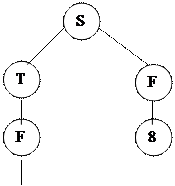
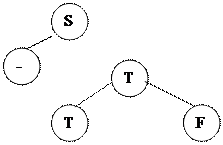
На основе рассмотренного выше примера деревья вывода для цепочек вывода 1 и 2. Эти деревья приведены на рис.20.

Рис. 20. Примеры деревьев вывода для грамматики

целых десятичных чисел со знаком

Для того чтобы построить дерево вывода, достаточно иметь цепочку вывода. Дерево вывода можно построить двумя способами: сверху вниз и снизу вверх. Для строго формализованного построения дерева вывода всегда удобнее пользоваться строго определенным выводом: либо левосторонним, либо правосторонним.

При построении дерева вывода сверху вниз построение начинается со стартового символа грамматики, который помещается в корень дерева. Затем в грамматике выбирается необходимое правило, и на первом шаге вывода корневой символ раскрывается на несколько символов первого уровня. На втором шаге среди всех концевых вершин дерева выбирается крайняя (крайняя левая – для левостороннего ввода, крайняя правая - для правостороннего) вершина, обозначенная нетерминальным символом, для этой вершины выбирается нужное правило грамматики, и она раскрывается на несколько вершин следующего уровня. Построение дерева заканчивается, когда все концевые вершины обозначены терминальными символами, в противном случае надо вернуться ко второму шагу и продолжить построение.

Построение дерева вывода снизу вверх начинается с листьев дерева. В качестве листьев выбираются терминальные символы конечной цепочки вывода, которые на первом шаге построения образуют последний уровень дерева. Построение дерева идет по уровням. На втором шаге построения в грамматике выбирается правило, первая часть которого соответствует крайним символам в уровне дерева (крайним правым символам при правостороннем выводе и крайним левым – при левостороннем). Выбранные вершины уровня соединяются с новой вершиной, которая выбирается из левой части правила. Новая вершина попадает в уровень дерева вместо выбранных вершин. Построение дерева закончено, если достигнута корневая вершина (обозначенная терминальным символом), а иначе надо вернуться ко второму шагу и повторять его над полученным уровнем дерева.

Поскольку все известные языки программирования имеют нотацию записи «слева - направо», компилятор также всегда читает входную программу слева направо (и сверху вниз, если программа разбита на несколько строк). Поэтому для построения дерева вывода методом «сверху вниз», как правило, используется левосторонний вывод, а для построения «снизу вверх» - правосторонний вывод. Нотация чтение программ «слева направо» влияет не только на порядок разбора программы компилятором, но и на порядок выполнения операций – при отсутствии скобок большинство равноправных операций выполняются в порядке слева направо, что имеет существенное значение.

Дата добавления: 2014-12-27