ВАЖНО!!! Все пиццы подаются на горячих тарелках (приблизительно 80 оС) !!! Это делается для того, чтобы на столе у гостей пицца как можно дольше сохраняла температуру. 2 страница

Преобразование двоичного числа в шестнадцатеричное число заключается в том, что биты, начиная с младшего значащего бита, объединяются в группы по четыре. Каждой группе подбирается соответствующий шестнадцатеричный символ. Например, чтобы представить двоичное число 101010111111101₂ в виде шестнадцатеричного числа необходимо слева добавить два незначащих нуля с целью формирования битов в группы по четыре: 0010 1010 1111 1101. Заменив каждую группу битов соответствующим шестнадцатеричным символом, получим число 2AFD₁₆.

Данная форма записи намного проще и воспринимается легче, чем двоичная.

Нужно помнить, что шестнадцатеричные числа – это способ представления двоичных чисел, которыми оперирует микропроцессор.

Представление шестнадцатеричного числа в виде двоичного также осуществляется по выражению (1.1).

2AFD₁₆ = 2*16³ + A*16² + F*16¹ + D*16⁰ =
2*4096 + 10*256 + 15*16 + 13*1 =

8192 + 2560 + 240 + 13 = 11005₁₀

10101011111101₂ = 1*2¹³ + 0*2¹² + 1*2¹¹ +0*2¹⁰ + 1*2⁹ +0*2⁸ +
+ 1*2⁷ + 1*2⁶ + 1*2⁵ + 1*2⁴ + 1*2³ + 1*2² +0*2¹ +1*2⁰ =
= 8192 + 0 + 2048 + 0 + 512 + 0 + 128 + 64 + 32 + 16 +
+ 8 + 4 + 0 + 1 = 11005₁₀

1.5. Двоичная арифметика

Четыре основные арифметические операции, а именно сложение, вычитание, умножение, деление можно выполнять в позиционной системе счисления с любым основанием.

Сложение двух двоичных чисел

a	b	a+b
1+1+1

Правила сложения двоичных и десятичных чисел аналогичны, но в результате более быстрого заполнения разрядов в двоичной системе счисления быстрее происходит и перенос в старший разряд при сложении двоичных чисел.

Прибавление единицы к старшему разряду в результате переполнения соседнего, младшего разряда называют переносом.

Сложение двоичных чисел выполняется по тем же правилам, что и сложение десятичных чисел. Например, сложение двоичных чисел 1101010 и 1101100 происходит следующим образом. В первом младшем разряде слагаемыми являются 0 и 0, результат получается 0. Во втором разряде к 1 прибавляется 0, результат получается 1. В третьем разряде к 0 прибавляется 1, результат получается 1. В четвертом разряде результатом сложения 1 с 1 является 10. Единицу переноса записываем над пятым разрядом, в котором суммирование 1,0 и 0 дает в результате 1. В шестом разряде снова суммируются 1 и 1, результат получается 10. Аналогичным образом единицу переноса записываем над седьмым разрядом, в котором теперь необходимо сложить три единицы. Результат есть 11. Единицу переноса располагаем над восьмым разрядом, который пуст для обоих слагаемых, поэтому в результате сложения в восьмом разряде появится 1. Порядок сложения приведен на рис.1.1.

Разряд
ЧислоА
Число В
Сумма

Разряд
Перенос				1
ЧислоА
Число В
Сумма					(1)0

Разряд
Перенос	1	1
ЧислоА
Число В
Сумма		(1)1	(1)0

Рис.1.1. Схема сложения двух чисел.

Вычитание двоичных чисел

Вычитание десятичных чисел является более привычным и на их примере можно понять механизм вычитания двоичных чисел. Например, вычтем 17283 (вычитаемое) из числа 909009 (уменьшаемого). Вычитание начинают с самого правого разряда. Вычитая 3 из 9, получаем 6.

Разряд
Число А
Число В
Разность

Разряд
Число А					(10)
Число В
Разность

Разряд
Число А		(10)
Число В
Разность

Рис.1.2. Схема вычитания двух десятичных чисел

В следующем разряде необходимо вычесть 8 из 0, что непосредственно сделать невозможно, так как 8 > 0. Чтобы осуществить дальнейшие вычисления необходимо обратиться к разрядам, расположенным слева, для нахождения числа, не равного 0. В данном случае таким числом будет 9. Занимаем 1 из 9, в результате чего в четвертом разряде вместо 9 появляется 8, в третьем разряде вместо 0 появляется 9, во втором разряде – 10.

Теперь во втором разряде из 10 можно отнять 8, получив 2. В третьем разряде нужно вычесть 2 из 9, получим 7. В четвертом разряде вычитаем 7 из 8, получаем 1. В пятом разряде нужно вычесть 1 из 0. Для этого необходимо опять занять 1, двигаясь влево до тех пор, пока не дойдем до первого ненулевого разряда. В нем 9 заменяем на 8, а вместо 0 в пятом разряде получаем 10. Теперь вычисления можно продолжить.

Для двоичных чисел процесс вычисления приведен на рис.1.3.

Разряд
ЧислоА				1
Число В
Разность

Разряд
ЧислоА							(10)
Число В
Разность

Разряд
ЧислоА				(10)
Число В
Разность

Результат вычисления в правом разряде 1-1 = 0. Во втором разряде вычесть 1 из 0 просто так не удастся, и поэтому просматриваем разряды справа налево до тех пор, пока не найдем 1. Добавляем 1 к 0 во втором разряде, что дает 10 (один, нуль). Числу 10₂ соответствует десятичное число 2. Нули, которые стоят между двумя разрядами, обращаются в единицы. Во втором разряде вычитаем из 10₂ – 1₂ и получаем 1₂. В третьем и четвертом разрядах результат вычитания будет равен 0.В пятом разряде опять из 0 нужно вычесть 1, для чего опять производится заем, как и в случае, описанном выше.

Если уменьшаемое больше вычитаемого, то разность получается положительной, если наоборот, то результат будет отрицательным.

Дополнительный код двоичного числа

Так как вычислительная машина оперирует с цифрами 0 и 1, то знаки + и -, предназначенные для обозначения положительных и отрицательных чисел, отсутствуют. Для представления положительных и отрицательных чисел в двоичной системе счисления и вычислительной технике используют старший значащий разряд двоичного числа. Если он равен 1, то число будет отрицательным, если он равен 0, то число будет положительное.

Такая форма представления чисел получается, если двоичное число представить следующим образом:

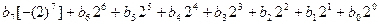
Такое представление называют дополнительным кодом двоичного числа. В этом случае старший значащий разряд имеет вес не 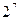, а 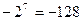. Если в этом разряде стоит 1, то он будет представлять десятичное число -128 и число в целом окажется отрицательным, так как наибольшее число, содержащееся в разрядах 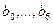, не может превысить десятичное значение 127.

Таким образом, двоичное число 10110001 можно представить как

1*(-128)+0*64+1*32+1*16+0*8+0*4+0*2+1*1=-79

Если в старшем значащем разряде стоит 0, подобная запись представляет собой положительное число, так как у всех остальных разрядов 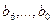веса положительны. Например,

01001000=0*(-128)+1*64+0*32+0*16+1*8+0*4+0*2+0*1=72

Для того чтобы представить отрицательное десятичное число в двоичной форме, необходимо это число записать как положительное в двоичном виде. После этого записать обратный код двоичного числа, а затем добавить к обратному коду двоичного числа единицу, в результате чего получим дополнительный код двоичного числа, который будет равен отрицательному десятичному числу. Рассмотрим следующий пример. Представить в двоичном виде отрицательное число – 77. Для этого получим двоичное число положительного числа 77.

77 = 01001101

Обратный код этого числа получим заменой 0 на 1, и 1 на 0.

Для получения дополнительного кода прибавим к обратному коду 1.

10110010 – обратный код
+ 1
10110011 – дополнительный код числа 77

Проверим, чему равно двоичное число 10110011

1*(-128)+0*64+1*32+1*16+0*8+0*4+1*2+1*1= -77

Таким способом можно представить числа в диапазоне от 10000000=-128 до 01111111=+127. Если этот диапазон недостаточен, то необходимо использовать шестнадцатиразрядные числа, которые образуются путем объединения двух 8-разрядных слов.

Использование дополнительных кодов двоичных чисел значительно упрощают операции двоичного вычитания, так как вычитание можно сложением положительного и отрицательного чисел. Например,

17-22= 17+(-22)

В двоичном виде это значит, что нужно сложить 00010001 = 17 и дополнительный код числа 00010110 = 22. Дополнительный код числа 00010110 получим, преобразовав его в обратный код 11101001 и прибавив к обратному коду 1.

00010110 – двоичный код числа 22

11101001 – обратный код
+ 1
11101010 – дополнительный код

После этого складываем

00010001 17

+
11101010 -22
=
11111011

Представим 11111011 в десятичном виде

1*(-128)+1*64+1*32+1*16+1*8+0*4+1*2+1*1= -5

Умножение двоичных чисел

Правила двоичного умножения

0*0=0
0*1=0
1*0=0
1*1=1

Умножение двух двоичных чисел осуществляется так же, как и умножение десятичных чисел. Возьмем два числа 9*3=27, в двоичном виде запишем их так

1001
* 11
=
1001
+ 1001
= 11011

11011= 1*16+1*8+0*4+1*2+1*1= 27

Двоично-десятичный код BCD (Binary Coded Decimal)

Двоично-десятичный код позволяет представлять в вычислительной машине десятичные цифры 0,…,9 с помощью символов двоичного алфавита.

При двоично-десятичном кодировании каждая десятичная цифра заменяется соответствующим 4-разрядным двоичным числом. Например, число 12 представляется следующим образом. Находим двоичное число для цифры 1 – 0001, находим двоичное число для цифры 2 – 0010, тогда двоично-десятичный код числа 12 будет иметь вид 0001 0010.

Системы кодирования

Для того чтобы иметь возможность оперировать не только с числами, но и символами, чтобы можно было представлять в ЭВМ текстовую информацию, используют системы кодирования, в которых каждому символу ставят в соответствие определенную комбинацию нулей и единиц.

В микроЭВМ наиболее часто используют два кода: американский стандартный код для обмена информацией ASCII (American Standard Code for Information Interchange) и расширенный двоично-кодированный EBCDIC (Extended Binary Coded Decimal Interchange).

Кроме этих кодов используются коды КОИ-7, КОИ-8 и др.

2. Схемотехника ЭВМ
2.1. Логические элементы

ЭВМ состоит не только из центрального процессора (микропроцессора). Он является главной, но лишь одной из многих интегральных микросхем, входящих в состав ЭВМ.

К наиболее распространенным интегральным микросхемам относятся логические элементы, реализующие логические функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, инверторы, исключающее ИЛИ, триггеры, регистры, счетчики.

Данные интегральные микросхемы являются цифровыми. На их входах могут появляться лишь два характерных уровня напряжения: низкое (около 0 В) и высокое (например, 5 В), причем низкий и высокий уровни напряжения представляют собой двоичные значения 0 и 1 соответственно.

Логический элемент И.

Условное графическое изображение логического элемента И представлено на рис.2.1.

Рис.2.1. Графическое изображение логического элемента И.

Так как это цифровая микросхема, то на входы 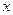и 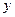подаются входные напряжения, которые могут принимать только фиксированные значения, принятые для данного типа микросхемы, которые определяются разработчиком микросхемы. Для микросхем типа ТТЛ это напряжения 0 В или 5 В. На выходе микросхемы 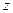также будут появляться данные напряжения, а какое конкретно – определяется таблицей истинности логического элемента. Для логического элемента И с двумя входами комбинации сигналов на входах элементов и таблица истинности представлены в таблицах 2.1 и 2.2.

Таблица 2.1 Комбинация сигналов на входах логического элемента И

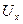,В	,В	,В

Таблица 2.2 Таблица истинности логического элемента И

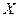
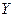
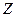
Таким образом, работа логического элемента И описывается следующим правилом: выходной сигнал равен 1 только тогда, когда все входные сигналы равны 1, т.е. 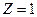только тогда, когда все 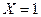, 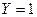. Если на одном их входов появляется 0, то и на выходе появляется 0. Это правило аналитически записывается в виде

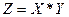(2.2)

то есть операция И записывается точкой.

Данная запись заимствована из алгебры Буля, которую можно рассматривать как арифметику систем, построенных на логических элементах.

В ЭВМ арифметико-логическое устройство содержит восемь двухвходовых логических элементов И, что позволяет микро-ЭВМ выполнять операцию над двумя словами А и В, каждое длиной 8 бит.

Логический элемент ИЛИ.

Условное графическое изображение логического элемента ИЛИ представлено на рис.2.2.

Рис.2.2. Графическое изображение логического элемента ИЛИ.

Выходной сигнал логического элемента ИЛИ равен 1, если хотя бы один из входных сигналов равен 1. Аналитически это записывается следующим образом:

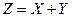(2.2)

Символ + обозначает выполнение операции ИЛИ. Таблица истинности логического элемента ИЛИ приведена в таблице 2.3.

Таблица 2.3 Таблица истинности логического элемента ИЛИ

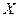
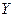
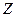
Инвертор или логический элемент НЕ

Выходной сигнал инвертора противоположен по значению входному сигналу или, другими словами, сигналы на входе и на выходе инвертора всегда не совпадают: если на входе 0, то на выходе 1; если на входе 1, то на выходе 0.

На рис.2.3 дано условное графическое изображение инвертора. Кружок на выходе инвертора означает выполнение операции НЕ.

Рис.2.3. Графическое изображение логического элемента НЕ.

Операция отрицания аналитически записывается в виде

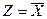(2.3)

Горизонтальная черта над переменной 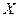читается как "не", т.е. 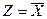читается как " 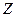равно не ".

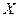Логический элемент И-НЕ

Логический элемент И-НЕ отличается от логического элемента И дополнительной операцией отрицания. Условное графическое изображение элемента такое же, как и у элемента И, с добавлением кружка на выходе (рис.2.4.)

Рис.2.4. Графическое изображение логического элемента И-НЕ.

В соответствии с алгеброй Буля операция И-НЕ аналитически записывается следующим образом:

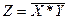(2.4)

Над переменным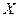и и 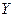сначала совершается операция И, результат которой инвертируется.

Правило работы логического элемента И-НЕ заключается в следующем: выходной сигнал равен 0, если все входные сигналы равны 1.

Логические элементы И-НЕ используются достаточно часто, так как любая логическая схема может быть построена исключительно на элементах И-НЕ, то есть можно обойтись элементом одного единственного типа.

Таблица истинности приведена в таблице 2.4.

Таблица 2.4 Таблица истинности логического элемента И-НЕ

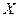
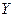
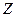
Логический элемент ИЛИ-НЕ

Условное графическое изображение приведено на рис.2.5.

Рис.2.5. Графическое изображение логического элемента ИЛИ-НЕ

Таблица истинности приведена в таблице 2.5

Таблица 2.5 Таблица истинности логического элемента ИЛИ-НЕ

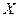
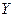
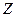
В логическом элементе ИЛИ-НЕ совмещено выполнение двух операций: ИЛИ и НЕ, при этом сначала выполняется операция ИЛИ, а затем производится инвертирование.

В логическом элементе ИЛИ-НЕ выходной сигнал равен 1, если все входные сигналы равны 0. Аналитически операция ИЛИ-НЕ записывается следующим образом:

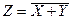(2.5)

Логический элемент ИСКЛЮЧАЮЩЕЕ ИЛИ

В логическом элементе ИСКЛЮЧАЮЩЕЕ ИЛИ выходной сигнал равен 1 только тогда, когда один из входных сигналов равен 1 (табл.2.6).

Таблица 2.6 Таблица истинности логического элемента
ИСКЛЮЧАЮЩЕЕ ИЛИ

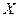
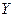
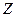
Условное графическое изображение приведено на рис.2.6.

Рис.2.6. Графическое изображение логического элемента
ИСКЛЮЧАЮЩЕЕ ИЛИ

2.2.Триггеры

Триггер представляет собой логическую схему с двумя выходами, значения сигналов на которых противоположны друг другу: если на одном из выходов 1, то на другом выходе 0 и наоборот. Выходы триггера обозначают 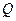и 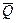; 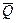по значению противоположно 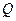( 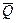читается как "не ").

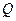Дата добавления: 2014-12-28