Необходимые сведения из теории

Исходные статистические данные.

Таблица 5.

Замечание. В статистической таблице представлены данные статистической отчетности по судимости в Российской Федерации за 2008 г. из формы № 10.1 «Результаты рассмотрения уголовных дел с учетом сложения наказаний» Судебного департамента по судам общей юрисдикции (без военных судов). В строках число осужденных учтено по основной статье приговора, вступившего в законную силу (по наиболее тяжкой статье), а в графах – по срокам лишения свободы в итоговом наказании (по совокупности преступлений или приговоров). Поэтому имеются значения по срокам лишения свободы, превышающим предел, допустимый по определенной категории тяжести преступлений.

Средняя величина - это обобщающий показатель, который характеризует качественно однородную совокупность по определенному количественному признаку. Например, средний возраст лиц, осужденных за кражу.

Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи, с чем каждый вариант приходится умножать на соответствующую численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту называют статистическим весом.

Средняя арифметическая простая – самый распространенный вид средней. Она равна сумме отдельных значений признака, деленной на общее число этих значений:

,

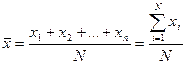где x₁,x₂, …,x_N – индивидуальные значения варьирующего признака (варианты), а N – число единиц совокупности.

Средняя арифметическая взвешенная применяется в тех случаях, когда данные представлены в виде рядов распределения или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов:

,

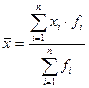где x_i – значение i–й варианты признака; f_i – частота i–й варианты.

Таким образом, каждое значение варианты взвешивается по своей частоте, поэтому частоты иногда называют статистическими весами.

Замечание. Если вычисление средней величины производят по данным, сгруппированным в виде интервальных рядов распределения, то сначала надо определить серединные значения каждого интервала х'_i, после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, где вместо x_i используется х'_i.

Вариация – это различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Показатели вариации используются для установления типичности средней величины, т. е. насколько точно характеризует средняя данную совокупность по определенному признаку.

К основным показателям вариации относятся следующие:

1) дисперсия;

2) среднее квадратическое отклонение;

3) коэффициент вариации.

Дисперсия определяется как средняя из отклонений, возведенных в квадрат.

Простая дисперсия для не сгруппированных данных:

.

Взвешенная дисперсия для вариационного ряда:

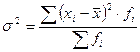
Замечание. На практике для вычисления дисперсии лучше использовать следующие формулы:

Для простой дисперсии

.

Для взвешенной дисперсии

Среднее квадратическое отклонение - это корень квадратный из дисперсии:

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем, однороднее совокупность и тем лучше средняя арифметическая отражает собой всю совокупность.

Коэффициент вариации – выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

Коэффициент вариации используют не только для сравнительной оценки вариации разных признаков или одного и того же признака в различных совокупностях, но и для характеристики однородности совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному распределению).

Дата добавления: 2014-12-23