
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 2. Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики
Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей: 1. Абсолютный прирост 2. Темп роста 3. Темп прироста 4. Значение 1% прироста.
В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными.
Важнейшим статистическим показателем является абсолютный прирост, который показывает абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между этими уровнями (между последующим и предыдущим уровнем, принятым за базу сравнения). Измеряется в тех же единицах, что и исходная информация.
А = Y1 – Y0,
где Y1 – значение отчетного уровня ряда динамики;
Y0 – значение базисного уровня ряда динамики.
Пусть мы имеем следующий ряд динамики производства продукции в 1990-1993 г.г.
| Год (t) | ||||
| Уровень производства продукции, тыс. руб. (Y) | 12,3 | 14,1 | 12,6 | 17,8 |
На основании данного ряда динамики рассчитаем базисные (приняв за базу сравнения 1990 год) и цепные абсолютные приросты:
Базисные: А91/90=Y91-Y90; А92/90= Y92-Y90; А93/90=Y93-Y90
Цепные: А91/90=Y91-Y90; А92/91= Y92-Y91; А93/92=Y93-Y92
Между цепными и базисными абсолютными приростами имеется следующая взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики:
А93/90=Y93-Y90=A91/90+A92/91+A93/92.
Темп (коэффициент) роста показывает относительную скорость роста уровня ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в %, а коэффициент роста - в долях.
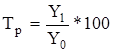 ,
, 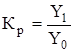 .
.
Между цепными и базисными темпами роста имеется взаимосвязь:
1. Произведение последовательных цепных темпов роста равно базисному темпу роста последнего периода:
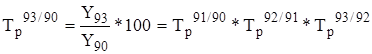 ;
;
2. Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:
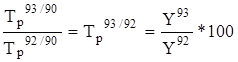 .
.
Темп (коэффициент) прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения:
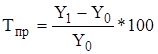 ,
, 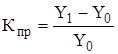 .
.
Между темпом (коэффициентом) прироста и темпом (коэффициентом) роста существует следующая взаимосвязь:
Тпр=Тр-100, Кпр=Кр-1.
Значение 1 % прироста определяется отношением абсолютного прироста к темпу прироста, и показывает сколько единиц в абсолютном выражении приходится на 1% прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он не имеет смысла (будет постоянной величиной).
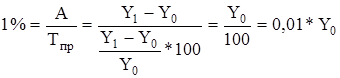 .
.
Расчет средних показателей ряда динамики.
Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины ряда динамики:
1. Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
В интервальных рядах динамики средний уровень определяется по формуле средней арифметической:
- простой 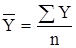 ;
;
- взвешенной 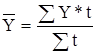 ,
,
где 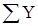 - сумма уровней; n – число уровней.
- сумма уровней; n – число уровней.
Для моментного ряда средний уровень определяется с помощью средней хронологической:
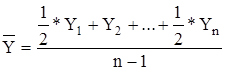 , где n – число уровней.
, где n – число уровней.
2. Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При цепном способе для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
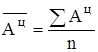 .
.
При базисном способе расчета чтобы определить средний абсолютный прирост, для этого определяется разность между конечным Уn и базисным У0 уровнями изучаемого периода, которая делится на m-1 субпериодов:
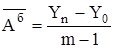 .
.
3. Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста цепным способом применяется следующая формула:
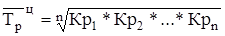 *100,
*100,
где Кр1, Кр2,..., Крn - индивидуальные (цепные) коэффициенты роста;
n - число индивидуальных темпов роста
Для базисного способа средний темп роста будет определяться по формуле:
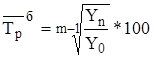 .
.
4. Средний темп прироста можно определить по формуле: 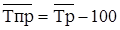 .
.
5. Среднее значение 1 % прироста определяется только для цепного способа по формуле:
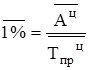 .
.
Эти показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.
|
|
Дата добавления: 2014-12-23; Просмотров: 426; Нарушение авторских прав?; Мы поможем в написании вашей работы!