Вопрос 3

Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда). На практике наиболее распространенными методами статистического изучения тренда являются: способ укрупнение интервалов (периодов), способ сглаживания скользящей средней, выравнивание ряда по среднегодовому абсолютному приросту, выравнивание ряда по среднегодовому темпу роста, аналитическое выравнивание при помощи способа наименьших квадратов.

1. Способ укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Сущность этого приема состоит в том, что данные или уровни за отдельные отрезки времени суммируются в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые), определяется средний уровень для полученного укрупненного периода. В результате после укрупнения периодов очевидной становится тенденция развития явления.

2. Способ скользящей средней. Скользящая средняя - это подвижная динамическая средняя, которая подсчитывается по динамическому ряду при последовательном передвижении на 1 год или на 1 интервал. Правильно исчисленная скользящая средняя устраняет в ряду динамики случайные колебания и дает возможность точнее выявить тенденцию в развитии, чем укрупненные интервалы.

3. Еще более точным способом является выравнивание по среднегодовому абсолютному приросту, которое рассчитывается по формуле:

,

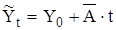где - выровненное значение;

Y₀ - начальный уровень ряда;

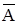- средний базисный абсолютный прирост, который вычисляется по формуле:

,

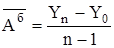где n - число лет;

t - порядковый номер года, в котором были приросты.

4. Выравнивание ряда по среднегодовому коэффициенту роста имеет следующий вид: ,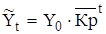

где - выровненное значение;

Y₀ - начальный уровень ряда

- среднегодовой базисный коэффициент роста, определяемый по формуле:

,

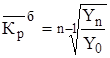n – число лет;

t - порядковый номер года.

5. Способом аналитического выравнивания можно получить обобщенную статистическую оценку тренда. Наиболее совершенным является способ наименьших квадратов, которому соответствует условие, что сумма квадратов отклонений фактического и теоретического уровней будет минимальной. Простейшим приемом является выравнивание ряда динамики по прямой: ,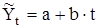

где а - свободный член;

b - коэффициент приращения;

t - период времени.

Способ наименьших квадратов дает систему двух нормальных уравнений для вычисления параметров функции:

,

,

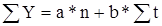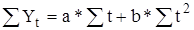где Y – исходные уровни ряда;

n – число членов ряда;

t – время.

Для упрощения вычислений показателям времени t придают такие значения, чтобы их сумма была равна нулю (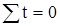). При этом используют следующие формулы:

- если ряд содержит четное число членов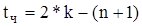

- если ряд содержит нечетное число членов ,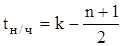

где k – порядковый номер года;

n – число лет в периоде.

При 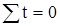система уравнений будет иметь следующий вид:

,

.

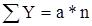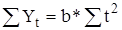Исходя из полученной системы уравнений найдем параметры уравнения прямой:

,

.

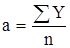Тема: Абсолютные и относительные величины

1. Абсолютные величины

2. Относительные величины

Абсолютные величины в определенных условиях места и времени размер явления, процесса.

Различают 2 вида абсолютных величин:

1. Индивидуальные - характеризуют размеры явления,

Абсолютные и относительные величины используют в экономических исследованиях.

Абсолютные величины – именованные числа, всегда имеют определенную размерность и определенную единицу измерения (натуральные, стоимостные, трудовые).

Натуральные выражаются в физических мерах: веса (кг, т), длины и площади (м, га). Также используют условно-натуральные единицы (условные га, условные головы, условные эталонные трактора).

Стоимостные выражаются в денежной форме: руб., тыс. руб., млн. руб.

Трудовые выражаются в: человеко-днях, человеко-часах, коне-днях, машино-днях.

На практике часто используют комбинированные единицы измерения: тонно-километры, пассажиро-километры, кВт-ч.

1. Относительные величины

Относительные величины – представляют собой показатели, выражающие меру количественных соотношений различных процессов и явлений.

Относительный показатель всегда представляет собой соотношение 2-х величин.

В относительных величинах используют различные базы сравнения:

1) доли (коэффициента), если базисная величина приравнивается к 1

2) в виде % (в случае, когда базисная величина равна 100)

3) промилле (в случае, когда базисная величина равна 1000)

4) продецимилле (в случае, когда базисная величина равна 10000)

В экономическом анализе различают следующие виды относительных величин:

1. Относительные величины выполнения плана рассчитываются как:

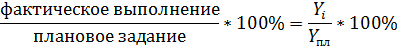
Числитель и знаменатель должны соответствовать одному и тому же периоду

2. Относительные величины планового периода рассчитываются как:

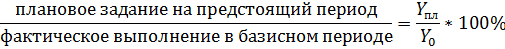
3. Относительные величины динамики рассчитываются как относительные случайные величины в определенный период времени, одноименные величине за один из прошлых периодов и называемые темпами роста. При этом, различают цепные и базисные темпы роста.

Цепные: 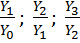и т.д.

Базисные: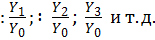

Относительные величины выражаются в коэффициентах или %. Между относительными величинами динамики планового задания и выполнения плана существует зависимость:

4. Относительные величины интенсивности (обычно именованные числа и имеют размерность тех величин, которые они отражают.)

Наиболее часто применяемые в практике относительные величины интенсивности: фондоотдача, производительность труда, рентабельность производства и т.д.

Фондоотдача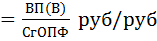

ПТ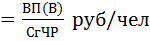

R=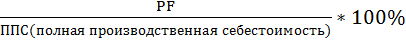

5. Относительные величины координации характеризуют отношение отдельных частей совокупности с одной из них принятой за базу сравнения, при этом из 2 сравниваемых частей за базу берется любая из них. Эти величины выражаются в %, промилле, отношениях в квадрате.

6.Относительные величины сравнения рассчитываются как отношение одноименных уровней различных объектов, взятых за один и тот же период или на один период времени. Эти величины выражаются в % или в кратных отношениях, показывающих во сколько раз одна сравниваемая величина больше или меньше другой.

7. Относительные величины структуры:

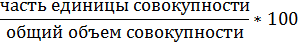
Дата добавления: 2014-12-23