Результаты расчетов показателей вариации

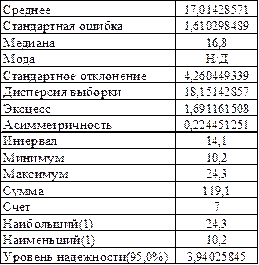
СПИСОК ЛИТЕРАТУРЫ

1. Глинский, В.В., Ионин, В.Г. Статистический анализ [Текст]: Учеб. пособие. – М.: Филин, 1998. – 264 с.

2. Громыко, Г.Л. Общая теория статистики: Практикум. [Текст]. – М.: ИНФРА-М, 1999. – 139 с.

3. Громыко, Г.Л. Теория статистики: практикум [Текст]. – М.: ИНФРА-М, 2001. – 160 с.

4. Гусаров, В.М. Теория статистики [Текст]: Учеб. пособие для ВУЗов. – М: Аудит, ЮНИТИ, 1998. – 247 с.

5. Ефимова, М.Р., Рябцев, В.М. Общая теория статистики. [Текст]. – М: Финансы и статистика, 1991. – 302 с.

6. Мармоза, А.Т. Практикум по математической статистике [Текст]: Учебное пособие. – К.: Выща школа, 1990. – 191 с.

7. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности [Текст]: Учебник / А.И. Харламов, О.Э. Башина, В.Т. Пабурин. Под ред. Спирина А.А., О.Э. Башиной / М.: Финансы и статистика, 1994. – 296 с.

8. Практикум по общей теории статистики [Текст]: Учеб. пособие / Н.Н. Ряузов и др. – 2-е изд. – М.: Финансы и статистика, 1981. – 278 с.

9. Салин, В.Н., Чурилова, Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля [Текст]: Учебник. – М.: Финансы и статистика, 2006. – 480 с.

10. Сборник задач по общей теории статистики [Текст]: Учебное пособие/ И.С. Пасхавер, А.Л. Яблочник, Н.Т.Иващенко и др. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1983. – 280 с.

11. Практикум по теории статистики [Текст]: /Под. ред. Р.А. Шмойловой – М.: Финансы и статистика, 1999. – 414 с.

12. Статистика [Текст]: Курс лекций / Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др. Под ред. к.э.н. В.Г. Ионина. – Новосибирск: изд-во НГА и У, 1996. – 310 с.

13. Статистик а [Текст]: Методические указания к выполнению практ. и лаб. работ. Часть 2 /Л.И. Бернасовская, Н.И. Гришакина, Г.В. Лебедева, О.Д. Притула, Г.В. Фетисова.- НовГУ им. Я.Мудрого, 2005.-56с.

14. Статистика рынка товаров и услуг [Текст]: Учебник / И.К. Белявский, П.Д. Кулагина, А.В. Коротков и др. Под ред. И.К. Белявской – М.: Финансы и статистика, 1995. – 432 с.

15. Статистика [Текст]: Учебное пособие./ А.В. Багат, М.М. Конкина, В.М. Симгира и др.; Под ред. В.М. Симгиры. – М.: Финансы и статистика, 2005. – 368 с.

16. Статистика [Текст]: Учебное пособие./ Под ред. проф. М.Р. Ефимовой. – М.: ИНФРА-М, 2000. – 336 с. – (Серия “Вопрос - ответ”).

17. Статистика [Текст]: Учебник/ И.И. Елисеева, И.И. Егорова и др.; Под ред. проф. И.и. Елисеевой. – М.: ТК Велби, Изд-во Проспект, 2003. – 448 с.

18. Теория статистики [Текст]: Учебник./ Под ред. профессора Г.Л. Громыко. – Москва: Инфра-М, 2000. – 414 с.

19. Теория статистики [ Текст]: Учебник./ Под ред. Р.А. Шмойловой.- 4-е издание, перераб. и доп. – М.: Финансы и статистика, 2004. – 656 с.

Приложение А

КРАТКИЙ СЛОВАРЬ ОСНОВНЫХ ПОНЯТИЙ

Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия и среднее квадратическое отклонение, квартильное отклонение.

Вариация – колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака – фактора.

Децили – варианты, делящие ранжированный ряд на десять равных частей.

Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины.

Закономерности распределения – закономерности изменения частот в вариационных рядах.

Квартили – значения признака, делящие ранжированную совокупность на четыре равновеликие части.

Квинтели –значения признака, делящие ранжированную совокупность на пять равновеликих частей.

Коэффициент вариации – процентное соотношение среднего квадратического отклонения к средней величине признака.

Коэффициент осцилляции (относительный размах вариации) – процентное соотношение размаха вариации к средней величине признака.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Критерии согласия – особые статистические показатели, характеризующие соответствие эмпирического и теоретического распределений. Известны критерии согласия К. Пирсона, В.И. Романовского, А.Н. Колмогорова, Б.С. Ястремского.

Линейный коэффициент вариации (относительное линейное отклонение) – процентное соотношение среднего линейного отклонения к средней величине признака.

Медиана – значение признака, приходящееся на середину ранжированной совокупности.

Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под действием признака – фактора, положенного в основание группировки.

Мода – значение изучаемого признака, повторяющееся с наибольшей частотой.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Относительные показатели вариации – это коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Перцинтили – значения признака, делящие ряд на сто частей.

Размах вариации – разность между наибольшим и наименьшим значениями варьирующего признака.

Среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Среднее квадратическое отклонение, дисперсия и среднее линейное отклонение могут определяться по формулам простой и взвешенной (в зависимости от исходных данных).

Среднее линейное отклонение – средняя арифметическая из абсолютных значений отклонений вариант признака от их средней.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающем влияние случайных факторов.

Эмпирическое корреляционное отношение – корень квадратный из эмпирического коэффициента детерминации.

Эмпирический коэффициент детерминации – доля межгрупповой дисперсии в общей дисперсии.

Энтропия – мера неопределенности данных наблюдения, которая может иметь различные результаты. Зависит от числа градаций признака и вероятности каждой их них.

Приложение Б

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое вариация признака в совокупности и в чем значение ее изучения?

2. В чем состоят различия в построении рядов распределения с дискретным и непрерывным характером вариации признака?

3. Какие группы обобщающих показателей используют для характеристики особенностей рядов распределения?

4. Как графически представить ряд распределения?

5. В чем состоят особенности расчета средней арифметической в вариационных рядах?

6. Как оценить степень неравномерности распределения признака?

7. В чем состоит значение относительных показателей вариации?

8. Что характеризуют показатели формы распределения?

9. Каковы особенности кривой нормального распределения?

10. В чем заключается разница между вариационным рядом и группировкой?

11. Какие показатели применяются для оценки асимметричности распределения?

12. Почему средняя арифметическая интервального ряда является приближенной средней, от чего зависит степень ее приближения?

13. Что представляет собой дисперсия альтернативного признака? Чему она равна?

14. Почему дисперсия и среднее квадратическое отклонение не всегда являются достаточными для характеристики вариации признака в изучаемых совокупностях?

15. На какие две большие группы делятся причины, факторы, вызывающие вариацию?

16. Что такое размах вариации, в чем его недостаток как показателя вариации?

17. Что представляет собой среднее линейное отклонение, в чем его недостатки как показателя вариации?

18. Что представляют собой медиана, квартили, децили, персентили?

19. Какой показатель используется для характеристики островершинности распределения?

20. Каким образом определяется существенность асимметрии и эксцесса?

Приложение В

ТЕСТОВые ЗАДАНия

1. Вариация – это:

а) изменение массовых явлений во времени;

б) изменение структуры статистической совокупности в пространстве;

в) изменение значений признака во времени и пространстве;

г) изменение состава совокупности.

2. Какой из показателей вариации характеризует абсолютный размер колеблемости признака около средней величины?

а) коэффициент вариации;

б) дисперсия;

в) размах вариации;

г) среднее квадратическое отклонение.

3. Что характеризует коэффициент вариации?

а) диапазон вариации признака;

б) степень вариации признака;

в) тесноту связи между признаками;

г) пределы колеблемости признака.

4. Если все значения признака увеличить в 16 раз, то дисперсия:

а) не изменится;

б) увеличится в 16 раз;

в) увеличится в 256 раз;

г) увеличится в 4 раза;

д) предсказать изменение дисперсии нельзя.

5. При анализе данных о дальности перевозок грузов морским транспортом получен коэффициент асимметрии As = 0,732 и показатель эксцесса Ex = 3,456. Это значит, что распределение:

а) нормальное;

б) имеет правостороннюю асимметрию;

в) имеет левостороннюю асимметрию;

г) островершинное;

д) плосковершинное.

6. Средний размер реализованной коммерческой организацией спортивной обуви равен 39, мода – 39, медиана – 39. На основании этого можно сделать вывод, что распределение проданной спортивной обуви по размеру:

а) симметричное;

б) приближенно симметричное;

в) с левосторонней асимметрией;

г) с правосторонней асимметрией;

д) данные не позволяют сделать вывод.

7. Количественно измерить закономерность распределения можно с помощью статистических характеристик:

а) центра распределения;

б) вариации;

в) асимметрии и эксцесса.

8. Среднее значение признака в двух совокупностях одинаково. Может ли быть различной вариация признака в этих совокупностях?

а) да;

б) нет.

9. Для измерения вариации в ряду несгруппированных данных используется:

а) размерность между крайними значениями;

б) среднее отклонение значений признака от центра распределения.

10. Распределение семей по числу детей в двух областях можно графически представить следующим образом:

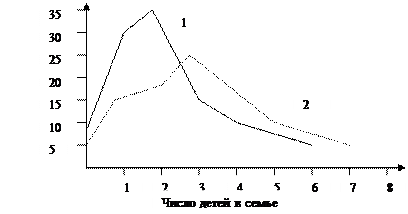Мода больше:

а) в первой области;

б) во второй области.

Вариация больше:

а) в первой области;

б) во второй области.

11. При расчете показателей вариации, изменяющих среднее отклонение значений признака от центра распределения, используется:

а) алгебраическая сумма отклонений индивидуальных значений признака от средней;

б) сумма абсолютных значений этих отклонений;

в) сумма квадратов этих отклонений.

12. Дисперсия может быть рассчитана:

а) только для количественного признака;

б) для количественного и атрибутивного признака.

13. Если в ряду распределения частоты заменить частостями, то дисперсия:

а) не изменится;

б) увеличится;

в) уменьшится;

г) предсказать изменение дисперсии нельзя.

14. Коэффициент асимметрии рассчитывается на основе центральных моментов распределения:

а) первого порядка;

б) второго порядка;

в) третьего порядка;

г) четвертого порядка.

15. Вычислены следующие показатели асимметрии для рядов распределения:

1. рабочих завода по проценту выполнения норм выработки As = 0,82;

2. магазинов торга по размеру товарооборота As = 0,02.

В каких случаях для описания характера распределения целесообразно использовать нормальную кривую?

а) 1,2;

б) 1;

в) 2;

г) –

Дата добавления: 2014-12-23