Функціонал оцінювання 2 страница

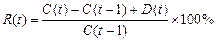, (4.1)

де C(t–1) — ціна ЦП в (t–1)-ий період, D(t) — дивіденди, нараховані в t-му періоді.

Сподівана норма прибутку цінних паперів

Введемо позначення:

Q = {q₁;q₂; …;q _n } — множина станів економічного середовища;

Р = { p ₁; p ₂; …; p_n } — розподіл ймовірностей станів економічного середовища;

R_i = { R_{i 1}; R_{i 2}; …; R_in } — множина значень норми прибутку і-го ЦП залежно від станів, що їх може приймати економічне середовище.

Величина

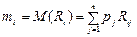(4.2)

має назву сподіваної норми прибутку і -го ЦП. Вона використовується в якості характеристики цього ЦП.

Приклад 1. Розглянемо дві акції виду А ₁ та А ₂. Для кожної з них можлива норма прибутку залежить від стану економіки. Експерти вказали на 5 можливих станів економіки, а також на ймовірність їх реалізації. Числові дані подано в табл. 4.1.

Таблиця 4.1

Стан економічного середовища	Ймовірність	Норма прибутку, % А 1 А2
Значне піднесення	0,1
Незначне піднесення	0,3
Стагнація	0,2
Незначна рецесія	0,3	– 2
Значна рецесія	0,1	– 10	– 5

Необхідно обчислити сподівану норму прибутку для цих ЦП.

Розв’язання. Сподівані норми прибутку позначимо відповідно через m ₁ та m ₂. Згідно з формулою (4.2) отримуємо, що m ₁ = 3,8%; m ₂ = 2,7%. Як бачимо, акція виду А ₁ характеризується вищою нормою прибутку, ніж акція виду А ₂, а тому, з точки зору максимізації прибутку, може бути обраною інвесторами акція виду А ₁.

Аналіз розв’язку. Невизначеність, пов’язана з величиною реалізованої норми прибутку, призводить до того, що інвестування в ЦП, а перш за все в звичайні акції, пов’язане з ризиком. Досить того, щоб настала стагнація або рецесія, тоді норма прибутку буде меншою, а прибуток перетвориться у збитки, причому ці збитки будуть більшими для акції виду А ₁. У зв’язку з цим слід зазначити, що акція виду А₁, приносячи більшу сподівану норму прибутку, обтяжена й більшим ризиком.

Якщо протягом Т періодів норма прибутку звичайної акції обчислюється згідно з формулою (1), то наближену оцінку сподіваної норми прибутку можна обчислити за формулою:

. (4.3)

Приклад 2. Розглянемо умовну акцію виду А, відносно якої маємо статистичну інформацію за останні 10 періодів (кварталів). Дані, а також обчислення норм прибутку, подано в табл. 4.2.

Користуючись формулами (4.1) та (4.2), отримуємо значення сподіваної норми прибутку для акції виду А: m _A = 0,1 × 43,29» 4,33 (%). -

Таблиця 4.2

Період	Ціна акції, грн.	Дивіденд, грн.	Приріст ціни, грн.	Прибуток, грн.	Норма прибутку, %
t	C (t)	D (t)	C (t) – C (t –1)	C (t)– C (t –1) + D (t)	R(t)
					6,9
					12,67
		4,5	– 10	– 5,5	– 3,33
					6,45
		4,5	– 8	– 3,5	– 2,16
					7,14
		4,5		4,5	2,81
					11,25
			– 7	-3	– 1,71
		3,5		5,5	3,27
Сума	43,29

Ризик цінних паперів в абсолютному вираженні

Другою, поряд із сподіваною нормою прибутку, важливою характеристикою кожного цінного паперу є його ризик. Що стосується системи кількісних оцінок ризику, то деякі з найбільш простих і важливих оцінок були приведені раніше. Однією з них є варіація (дисперсія). У даному випадку можна говорити про варіацію (дисперсію) норми прибутку цінного паперу. Для і -го ЦП її можна обчислити за формулою:

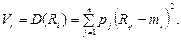(4.4)

Варіація (дисперсія) норми прибутку ЦП виражається у відсотках, піднесених до квадрата. Це, взагалі кажучи, дещо незручно з точки зору інтерпретації результатів. Цієї незручності позбавлена інша характеристика ступеня ризику — середньоквадратичне відхилення норми прибутку ЦП:

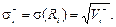
У випадку, коли є інформація про норму прибутку і -го ЦП у минулі Т періодів, варіацію можна обчислити за формулою:

.

Приклад 3. Виходячи з умови прикладу 1, обчислити ризик в абсолютному вираженні для кожного з ЦП виду А ₁ та А ₂ та порівняти їх між собою.

Розв’язання. Враховуючи, що m ₁ = 3,8%, m ₂ = 2,7%, згідно (4.4) отримуємо:

V₁ = 67,56; V₂ = 13,81;

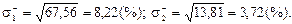
Як бачимо, ступінь ризику, пов’язаного з акцією виду А ₁, яка характеризується вищою сподіваною нормою прибутку, є значно вищим, ніж ризик, яким обтяжена акція виду А ₂.

Ризик цінних паперів у відносному вираженні

Розглянемо два цінних папери виду A ₁(m ₁; s₁) та A ₂(m ₂; s₂). Якщо для їх характеристик виконуються співвідношення m ₁ > m ₂ та s₁ < s₂, то в цьому випадку можна вважати, що ЦП виду A ₁ є кращим за ЦП виду A ₂ (символічно: A ₁f A ₂).

Якщо ж m ₁ > m ₂ і при цьому s₁>s₂, то для порівняння ризику цих ЦП можна скористатись однією з відносних оцінок ризику:

· коефіцієнт варіації:

; (4.5)

· коефіцієнт семіваріації:

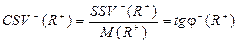; (4.6)

· модифікований коефіцієнт варіації:

; (4.7)

· модифікований коефіцієнт семіваріації:

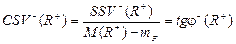, (4.8)

де m_F — норма прибутку безризикових або майже безризикових ЦП (наприклад, державних короткострокових облігацій, ЦП «старих фірм» тощо)

Приклад 4. Виходячи з умови прикладу 1, обчислити ризик у відносному вираженні для кожного із ЦП виду A ₁ та A ₂ і порівняти їх між собою.

Розв’язання. Оскільки згідно з умовою m ₁ = 3,8 > 2,7 = m ₂; s₁ = 8,22 > 3,72 = s₂, то для порівняння ЦП виду A ₁ та A ₂ скористаємось відносною оцінкою ризику, а саме — коефіцієнтом варіації:

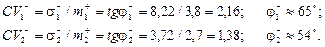
Рис. 4.1. Геометрична інтерпретація коефіцієнта варіації

На рис. 4.1 в системі координат «норма прибутку — ризик» акціям виду А ₁ відповідає точка А ₁ (m ₁;s₁), акціям виду А ₂ — точка А ₂(m ₂; s₂), тобто їм відповідають радіуси-вектори та .

Враховуючи, що коефіцієнт варіації має негативний інгредієнт, приходимо до висновку, що з позиції цієї міри ризику перевага надається тим акціям, для яких відповідний радіус-вектор має менший кут нахилу до осі абсцис, тобто перевага надається ЦП виду А ₂.

Приклад 5. Виходячи з умови прикладу 1, а також враховуючи, що норма прибутку державних облігацій m_F = 3%, обчислити ризик кожного з цінних паперів виду А ₁ та А ₂ і порівняти їх між собою.

Розв’язання. Скористаємось модифікованим коефіцієнтом варіації (рис. 4.2):

Враховуючи, що коефіцієнт варіації має негативний інгредієнт, перевагу слід надати акціям виду А₁.

Рис. 4.2. Геометрична інтерпретація модифікованого коефіцієнта варіації

Отриманий результат суперечить висновкам, зробленим у прикладі 3. Ця суперечність пояснюється тим, що модифікований коефіцієнт варіації за своєю суттю здійснює «фільтрацію» ЦП, відкидаючи ті акції, норма прибутку яких менша від фіксованої норми прибутку.

Зауваження 1. На рис. 4.1 наведено акції виду A ₃(m ₃; s₃) та A ₄(m ₄; s₄), для яких m ₃ = m ₄ < 0 та s₃ > s₄, але при цьому 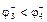. У цій ситуації для порівняння акцій формально скористаємось відносною оцінкою ризику (коефіцієнтом варіації чи семіваріації). З урахуванням того, що 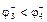, приходимо до висновку, що A ₃ f A ₄. Але здоровий глузд підказує, що має місце співвідношення A ₄ f A ₃.

Тому приходимо до висновку про недоцільність використання коєфіцієнта варіації (чи семіваріації) для порівняння ЦП у випадку, коли M (R⁺) < 0.

Слід також мати на увазі, що саме така ситуація виникла під час вивчення деяких ЦП Українських підприємств, виставлених на аукціон.

Аналогічна ситуація може виникнути і при використанні модифікованого коефіцієнта варіації (чи семіваріації). На рис. 4.2 порівняння ЦП виду A ₂ та A ₃ (які знаходяться в лівій півплощині по відношенню до прямої m = m_F) також приводить до протиріччя. А тому модифікований критерій слід використовувати лише для порівняння ЦП, що знаходяться праворуч по відношенню до прямої m = m_F (m = 3).

Кореляція цінних паперів та її застосування

Під час формування ПЦП істотну роль відіграє ще одна характеристика — кореляція ЦП. Вона характеризує взаємозв’язок між нормами прибутку двох цінних паперів. Міру щільності цього взаємозв’язку вимірюють за допомогою коефіцієнта кореляції.

Коефіцієнт кореляції є показником того, наскільки зв’язок між нормами прибутків акцій двох видів близький до строгої лінійної залежності. Він однаково ураховує і надто велику частку випадковості, і надто велику частку нелінійності цього зв’язку. Якщо розглядаються дві звичайні акції виду А ₁та А ₂, то їхній коефіцієнт кореляції визначається за формулою:

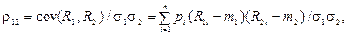
де r₁₂ — коефіцієнт кореляції для акцій виду А ₁ та А ₂, cov(R ₁, R ₂) — коваріація випадкових величин R ₁ та R ₂. Очевидно, що cov(R_k, R_k) = 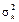, r _kk = 1, k = 1, 2.

Якщо коефіцієнт кореляції не дорівнює нулю, то він своєю величиною характеризує не тільки наявність, а й тісноту стохастичного зв’язку між R ₁ та R ₂.

Нагадаємо основні властивості коефіцієнта кореляції:

• коефіцієнт кореляції приймає значення в межах [– 1; 1];

• абсолютна величина коефіцієнта кореляції вказує на тісний взаємозв’язок норм прибутку акцій: чим більшою (ближчою до одиниці) є абсолютна величина, тим тісніше пов’язані між собою ці акції і чим меншою (ближчою до нуля) вона є, тим слабшим є зв’язок між цими акціями;

• знак коефіцієнта кореляції вказує напрямок взаємозв’язку норм прибутку акцій. Якщо він додатний, то маємо додатну кореляцію, коли зростання (зниження) норми прибутку однієї акції відбувається одночасно із зростанням (зниженням) норми прибутку другої акції. Коли ж коефіцієнт кореляції є від’ємною величиною, то маємо коефіцієнт так званої від’ємної кореляції акцій, коли зростання (зниження) норми прибутку однієї акції відбувається одночасно із зниженням (зростанням) норми прибутку другої.

Приклад 5. Розглянемо три різні акції виду А ₁, А ₂, А ₃. Дані стосовно їх норм прибутку та ймовірностей подано в табл. 4.3.

Необхідно обчислити відповідні коефіцієнти кореляції.

Таблиця 4.3

Стан економіки	Імовірність	Норма прибутку акцій, % А1 А2 А3
Значне піднесення	0,1
Незначне піднесення	0,3
Стагнація	0,3
Незначна рецесія	0,2
Значна рецесія	0,1	–10

Розв’язання. Після відповідних обчислень одержимо такі значення сподіваних норм прибутку та середньоквадратичних відхилень акцій:

m ₁ = 5,5%, m ₂ = 13%, m ₃ = 8%; s₁ = 7,567%, s₂ = 8,718%, s₃ = 1,732%.

Знайдемо коваріацію між нормами прибутку для акцій А ₁ та А ₂:

cov(R ₁, R ₂) = 0,1 × (20 – 5,5)(30 – 13) + 0,3 × (10 – 5,5)(20 – 13) +
+ 0,3 × (5 – 5,5)(10 – 13) + 0,2 × (0 – 5,5)(5 – 13) + 0,1 × (– 10 – 5,5)(0 – 13) = 63,5.

Аналогічно знаходимо коваріації між нормами прибутку акцій виду А ₁ та А ₃, А ₂ та А ₃:

cov(R ₁, R ₃) = – 13;cov(R ₂, R ₃) = – 14.

Знайдемо тепер відповідні коефіцієнти кореляції:

r₁₂ = cov(R ₁, R ₂)/s₁s₂ = 63,5 / (7,567 × 8,718) = 0,963;

r₁₃ = cov(R ₁, R ₃)/s₁s₃ = – 13 / (7,567 × 1,732) = – 0,992;

r₂₃ = cov(R ₂, R ₃)/ s₂s₃ = – 14 / (8,718 × 1,732) = – 0,927.

На практиці додатна кореляція зустрічається значно частіше, ніж від’ємна. Це пов’язано з так званою силою прискорення ринку. Наприклад, дослідження, проведені на Нью-Йоркській біржі, показали, що переважна частина акцій має коефіцієнт кореляції в межах від 0,4 до 0,6.

Аналогічно тому, як це було зроблено при обчисленні сподіваної норми прибутку та ризику, оцінку коефіцієнта кореляції для двох видів акцій — вибірковий коефіцієнт кореляції — можна знайти на основі інформації про норми прибутку акцій у минулому.

Формула для обчислення вибіркового коефіцієнта кореляції двох видів акцій така:

,

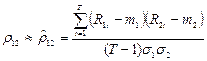де Т — кількість попередніх періодів, для яких маємо інформацію.

У зв’язку з випадковістю вибірки, вибірковий коефіцієнт кореляції може відрізнятися від нуля навіть тоді, коли між спостережуваними випадковими величинами відсутня кореляція.

Портфель цінних паперів

Узгодження максимізації норми прибутку і мінімізації ризику не є простим, оскільки на досить ефективному ринку цінні папери з високою нормою прибутку характеризуються відповідно високим ступенем ризику. Розсудливий інвестор шукає такі можливості щодо розміщення капіталу, при яких із збільшенням норми прибутку одночасно зменшувався б і ступінь ризику. Такі можливості дає йому формування портфеля цінних паперів. Сукупність придбаних цінних паперів становить портфель. Під структурою портфеля цінних паперів розуміють співвідношення часток інвестицій у цінні папери різних видів.

Математична модель ПЦП, сформованого з N цінних паперів, будується таким чином. Нехай R_k — норма прибутку k -го виду ЦП (k = 1, …, N), S_k — обсяг грошових активів, інвестованих в k- тий вид ЦП, S — обсяг всіх грошових активів, інвестованих в ПЦП. Покладемо

х_k = S_k / S, k = 1, …, N,

тобто х_k — це частка інвестицій у ЦП k -го виду. Очевидно, що x_k ³0 і при цьому

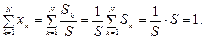
Структуру ПЦП відображає вектор X = { x ₁; ...; x_N }.

Тоді норма прибутку ПЦП, складеного з N видів ЦП

Cподівана норма прибутку цього ПЦП

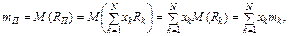
тобто

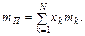
Ризик ПЦП згідно з класичним підходом обчислюється на основі дисперсії його норми прибутку:

V_П = D (R_П) = s²(R_П) = 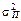= M (R_П – m_П)².

Легко показати [3], що

,

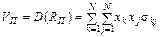де .

Однорідний портфель цінних паперів

Особливим випадком портфеля є однорідний портфель, тобто такий, який містить лише один вид цінних паперів.

Тоді для цього ПЦП

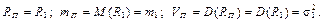
Портфель з двох видів цінних паперів

Нехай х ₁ та х ₂ частки інвестицій у ЦП виду А ₁ та А ₂, що складають портфель. Тоді, враховуючи що N = 2, отримуємо:

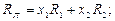
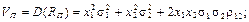
З урахуванням того, що х ₂ = 1 – х ₁, отримуємо:

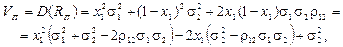(4.5)

тобто цільова функція V_П є функцією однієї змінної х ₁, а саме — параболою 2-го порядку. Оскільки х ₁ Î [0; 1], то для всіх значень параметрів s₁, s₂ і r₁₂ ця парабола проходить через точки А ₁(1; ) та А ₂(0; ), які відповідають однорідним ПЦП, складеним, відповідно, з ЦП виду А ₁ та виду А ₂.

Оскільки коефіцієнт кореляції r₁₂ приймає значення з проміжку [– 1; 1], то величина 1 – r₁₂ ³ 0. А тому коефіцієнт при 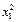для функції V_П

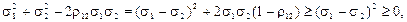
тобто парабола (4.5) є опуклою вниз і досягає свого мінімального значення у вершині . Функція V_П згідно зі своєю побудовою може набувати лише невід’ємних значень, а тому приходимо до висновку, що в системі координат (х ₁; V_П) вся парабола (4.5) лежить над віссю абсцис (рис. 4.3).

Надалі для визначеності щодо акцій виду A₁ та A₂ будемо вважати, що мають місце співвідношення:

М (R ₁) = m ₁ > m ₂ = М (R ₂);
s(R ₁) = s₁ > s₂ = s(R ₂).

Координати вершини параболи 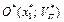обчислюються за формулами [4]:

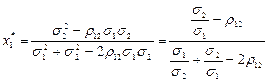; (4.6)

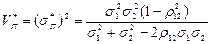(4.7)

Згідно з системою рівнянь

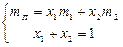
отримуємо, що

.

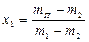Тоді

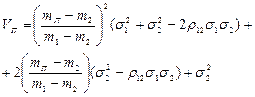. (4.8)

Отже, зв’язок між ризиком ПЦП V_П та його сподіваною нормою прибутку m_П також описується параболою другого порядку, і при цьому коефіцієнт при (m_П)² також набуває невід’ємного значення.

Легко переконатись, що графік функції (4.8) проходить через точки А ₁(m ₁; ) та А ₂(m ₂; ) (рис. 4.4).

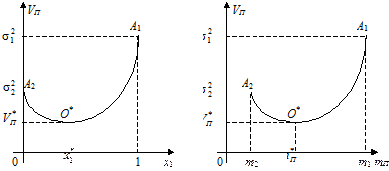
Рис. 4.3. Залежність ризику ПЦП від х 1(частки акції першого виду в ПЦП)

Рис. 4.4. Залежність ризику ПЦП від mП (сподіваної норми прибутку ПЦП)

Парабола (4.8) має вершину 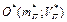, де

,

а значення 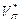обчислюється згідно з (4.7).

Сутність ефекту від диверсифікації при побудові ПЦП полягає в тому,що збільшення сподіваної норми прибутку m_П (починаючи з мінімально можливого допустимого значення) може привести (на певному етапі) до зменшення ризику V_П цього портфеля.

Згідно з рис. 4.4. при збільшенні m_П від значення m ₂ до m_П^* величина ризику ПЦП зменшується від 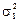до 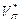= (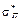)². Подальше збільшення m_П (від до m ₁) призводить до збільшення величини ризику портфеля (від (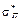)² до 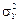). Отже, диверсифікація буде ефективною лише в тому разі, коли абсциса вершини О^* параболи (4.8) буде належати проміжку [ m ₂; m ₁] і, відповідно, абсциса вершини О^* параболи (4.5) — проміжку (0; 1).

Оскільки 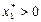, то з (4.6) випливає, що , тобто що r₁₂ Î [– 1; s₂/s₁). А тому можна зробити наступний висновок: для ПЦП, складеного з двох видів ЦП, диверсифікація дає ефективний результат щодо зменшення величини ризику лише в тому разі, коли коефіцієнт кореляції для норм прибутку цих ЦП r₁₂ Î [–1;r¢), де r¢ = .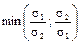

Приклад 6. Сподівана норма прибутку акцій виду А ₁ становить 60%, ризик цих акцій (середньоквадратчне відхилення) — 20%. Для акцій виду А ₂ відповідно сподівана норма прибутку — 40%, ризик — 15%. Коефіцієнт кореляції для цих акцій r₁₂ = 0,35. На основі цих акцій створюється ПЦП. Необхідно:

1) обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А₁ складають 20% вартості цього портфеля;

2) обчислити сподівану норму прибутку та ризик ПЦП, якщо акції виду А₁ складають 80% вартості ПЦП;

3) створити оптимальний ПЦП (тобто такий, що має мінімальний ризик).

Розв’язання. 1) Згідно з умовою частка акцій виду А ₁ в ПЦП х ₁ = 0,20, а тому частка акцій виду А ₂ х ₂ = 0,80. Тоді

2) Оскільки в цьому випадку х ₁= 0,80, х ₂ = 0,20, то отримуємо:

3) Оскільки 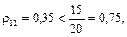то

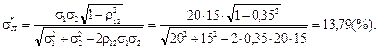
Приклад 7. Виходячи з умови прикладу 6, знайти структуру ПЦП:

а) сподівана норма прибутку якого становила б 50%; б) ризик якого становив би 16%.

Дата добавления: 2014-12-23