Порядок выполнения работы. Погрешности вычислений

Погрешности вычислений

Лабораторная работа № 2

Цель. Научиться решать прямую задачу теории погрешностей: научиться оценивать погрешность вычислений по действиям и с помощью дифференциального исчисления. Научиться решать обратную задачу теории погрешностей. Научиться округлять полученный результат.

Задание 1. Прямая задача теории погрешностей. Вычислить приближенное значение для функции нескольких переменных, оценить погрешность вычисления по действиям. Вычислить погрешность приближенного значения функции средствами дифференциального исчисления. Выполнить округление приближенного значения функции в соответствии с полученной оценкой погрешности.

Задание 2. Обратная задача теории погрешностей. Выяснить, используя принцип равных влияний, какой должна быть абсолютная погрешность переменных, для того чтобы погрешность функции не превышала 0,001.

1. Создать m-файл. Вычислить приближенное значение функции . Вычислить абсолютную и относительную погрешность функции по действиям, используя следующие формулы:

, , ,

,

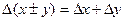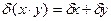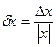– переход от относительной погрешности к абсолютной,

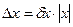– переход от абсолютной погрешности к относительной,

.

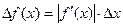m-file имеет вид:

a=4.07

b=2.6

c=3.7

adel=0.01

bdel=0.05

cdel=0.03

f=((a-c)*(b^2))/cos(4*c)

fdel=(((adel-cdel)/abs(a+c))+((abs(4*sin(4*c))*cdel)/abs(cos(4*c)))+((2*bdel)/abs(b)))*(abs((a-c)*(b^2)/cos(4*c)))

Fdel=fdel/abs(f)

После выполнения программы на экран выводятся значения переменных:

a =4.0700

b =2.6000

c =3.7000

adel =0.0100

bdel =0.0500

cdel =0.0300

f =-4.0647

fdel =0.7707

Fdel =0.1896

2. Создать m-файл. Вычислить приближенное значение функции . Вычислить абсолютную и относительную погрешность функции с помощью дифференциального исчисления, используя формулы:

; .

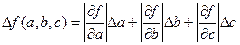m-file имеет вид:

a=4.07

b=2.6

c=3.7

adel=0.01

bdel=0.05

cdel=0.03

CHa=b^2/cos(4*c)

CHb=2*(a-c)*b/cos(4*c)

CHc=b^2/cos(4*c)+4*(a-c)*b^2/cos(4*c)^2*sin(4*c)

f=((a-c)*(b^2))/cos(4*c)

fdel=abs(CHa)*adel+abs(CHb)*bdel+abs(CHc)*cdel

Fdel=fdel/abs(f)

После выполнения m-file на экран выведется значения переменных:

a =4.0700

b =2.6000

c =3.7000

adel =0.0100

bdel =0.0500

cdel =0.0300

СHa =-10.9856

CHb =-3.1267

CHc =9.8414

f =-4.0647

fdel =0.5614

Fdel =0.1381

3. Выяснить значащие и верные цифры в приближенном значении функции , ориентируясь на большую из абсолютных погрешностей D, найденных в первом и втором пунктах. Выполнить округление приближенного значения функции. Вычислить полную погрешность вычислений, используя формулы:

; .

m-file имеет вид:

a=4.07

b=2.6

c=3.7

adel=0.01

bdel=0.05

cdel=0.03

CHa=b^2/cos(4*c)

CHb=2*(a-c)*b/cos(4*c)

CHc=b^2/cos(4*c)+4*(a-c)*b^2/cos(4*c)^2*sin(4*c)

f=((a-c)*(b^2))/cos(4*c)

fdel=abs(CHa)*adel+abs(CHb)*bdel+abs(CHc)*cdel

Fdel=fdel/abs(f)

okr_f=f-fdel

okr_del=abs(f-okr_f)

poln_del=fdel+okr_f

После выполнения m-file на экран выведется значение переменных:

a =4.0700

b =2.6000

c = 3.7000

adel =0.0100

bdel =0.0500

cdel =0.0300

CHa =-10.9856

CHb =-3.1267

CHc =9.8414

f = -4.0647

fdel =0.5614

Fdel =0.1381

okr_f =-4.6261

okr_del =0.5614

poln_del =-4.0647

4. Создать m-файл. Решить обратную задачу теории погрешностей: вычислить, используя принцип равных влияний, какими должны быть абсолютные погрешности переменных, для того чтобы погрешность функции не превышала 0,001. Использовать формулы:

, , .

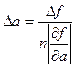m-file имеет вид:

a=4.07

b=2.6

c=3.7

CHa=b^2/cos(4*c)

CHb=2*(a-c)*b/cos(4*c)

CHc=b^2/cos(4*c)+4*(a-c)*b^2/cos(4*c)^2*sin(4*c)

f=-4.0647

fdel= 0.5614

Fdel=0.1381

adel=fdel/(3*abs(CHa))

bdel=fdel/(3*abs(CHb))

cdel=fdel/(3*abs(CHc))

После выполнения m-file на экран выведется значение переменных:

a=4.07

b=2.6

c=3.7

CHa=b^2/cos(4*c)

CHb=2*(a-c)*b/cos(4*c)

CHc=b^2/cos(4*c)+4*(a-c)*b^2/cos(4*c)^2*sin(4*c)

f=-4.0647

fdel= 0.5614

Fdel=0.1381

adel=fdel/(3*abs(CHa))

bdel=fdel/(3*abs(CHb))

cdel=fdel/(3*abs(CHc))

5. Составить отчет о выполнении лабораторной работы.

Замечание. В случае затруднений при вычислении частных производных можно использовать возможности символьных вычислений в Matlab.

Пример вычисления частных производных функции нескольких переменных в Matlab в символьном виде.

Код программы:

syms a b c % переменные a, b, c объявляются символьными

f=(a^2+b^(1/3))/(12*cos(x)) % создается функция в символьном виде

diff(f,a) % находится частная производная функции 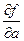в символьном виде

diff(f,b) % находится частная производная функции в символьном виде

diff(f,c) % находится частная производная функции 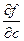в символьном виде

Вариант		a	b	c
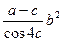
		4.07±0.01	2.6±0.05	3.7±0.03

Российский государственный университет инновационных технологий и предпринимательства

Пензенский филиал

Отчёт о лабораторной работе №2 по дисциплине «Математика»

Дата добавления: 2015-01-03