Изучение скольжения тележки по наклонной плоскости

Лабораторная работа №1

Цель работы.

1. Экспериментальная проверка равноускоренности движения тележки по наклонной

плоскости.

2. Определения ускорения свободного падения.

Теоретические основы лабораторной работы.

Как известно, при равноускоренном движении тела вдоль оси Ox проекция его скорости

vx от времени t определяется выражением

vx (t) = v 0 x + ax t (1)

где v 0 x

- проекция скорости на ось Оx в начальный момент времени. Зависимость координаты x от

времени t имеет вид

x = x

a t 2

+ v t + x. (2)

0 ox

 

Рассмотрим тележку, скользящую по наклонной плоскости (рис. 1.). Второй закон Ньютона, описывающий движение тележки:

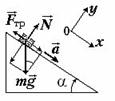
r r

РИС.1.

ma = mg + N + F òð, (3)

где N – сила реакции опоры, а сила трения скольжения F тр = m N. Проекции уравнения (3) на координатные оси:

Oy: N = mg cos a;

Ox: ma = mg sin a - m mg cos a;

где a – угол между наклонной плоскостью и горизонтом. Из последнего уравнения следует

a = g sin a - m g cos a. (4)

Описание установки

Общий вид экспериментальной установки показан на рис.2.

РИС.2.

1. рельс с сантиметровой шкалой на лицевой стороне;

2. тележка;

3. воздушный насос;

4. источник питания насоса ВС 4-12;

5. опоры рельса;

6. опорная плоскость;

7. фиксирующий электромагнит;

8. оптические ворота;

9. цифровой измерительный прибор ПКЦ-3;

10. пульт дистанционного управления;

11. угольник.

По рельсу 1 скользит тележка 2. Для уменьшения трения между поверхностями рельса и

тележки создается воздушная подушка с помощью воздушного насоса 3, подключенного к источнику питания 4. Высота рельса над опорной плоскостью 6 регулируется с помощью винтовых ножек опор 5. Электромагнит 7 фиксирует тележку в начале шкалы. Тележка снабжена флажком с черными вертикальными рисками. Цифровой измерительный прибор 9 фиксирует момент времени, скорость и ускорение тележки при прохождении флажка через оптические ворота 8. Запуск тележки и изменение режимов осуществляется пультом дистанционного управления 10. Угольник 11 используется для измерения вертикальной координаты точек рельса.

Порядок выполнения работы.

Упражнение 1. Измерение ускорения тележки при движении по рельсу с фиксированным углом наклона.

1. Выбрать на источнике питания воздушного насоса напряжение 12 В и включить насос (тумблер

«сеть» на источнике). Установить направляющий рельс горизонтально. Для этого поместить

тележку на рельс около точки с координатой 0,6 м (приблизительно в середине рельса) и, вращая винт правой опоры, добиться неподвижности тележки. Выключить насос.

2. Установив угольник вертикально на опорной плоскости, измерить с его помощью вертикальные

координаты h 0 и

h 0¢верхнего края шкалы, соответственно, в точках x = 0,220 м и x ¢= 1,000 м.

Измеренные величины h 0, h 0¢занести в таблицу 1.

Таблица 1.

x, м	x ¢, м	h 0, мм	h 0¢, мм

Приборные погрешности: D x

=D x ¢=1 мм, D h =0

D h 0¢= 0,5 мм.

3. Под обе ножки левой опоры подложить стандартную пластину толщиной d» 1 см.

4. Включить тумблер цифрового прибора (на правой боковой панели). Нажать последовательно

кнопки на пульте управления: «режим работы: 0», «механика: сброс», «индикация: время t1,t2».

5. Установить первые оптические ворота на x1 = 0,150 м, вторые – на x2 = 0,400 м. Установить на

источнике питания напряжение 4 В.

6. Нажать кнопку «механика: сброс». Включить воздушный насос. Тележку установить в крайнем

левом положении и зафиксировать электромагнитом. Нажать кнопку «механика: пуск». Тележка начнет двигаться, последовательно пройдет левые и правые оптические ворота и на дисплее прибора отразятся промежутки времени t1 и t2 от начала движения до прохождения ворот. Выключить воздушный насос. Величины x1, x2, t1,t2 занести в таблицу 2.

Таблица 2.

№ опыта	Измеренные величины	Рассчитанные величины
x 1, м	x 2, м	t 1, с	t 2 ,, с	2(x 2 - x 1) м	(t - t 1) с 2 2 2

Приборные погрешности: D x 1 = D x 2 = 5 мм, D t 1 = D t 2 = 0, 05 с.

7. Установить вторые оптические ворота последовательно в точках x2 = 0,500 м; 0,700 м; 0,900 м;

1,100 м и для каждого положения выполнить пункт 6.

Упражнение 2. Исследование зависимости ускорения тележки от угла наклона плоскости к горизонту. Определение ускорения свободного падения.

1.Установить первые оптические ворота на x 1 = 0,150 м, вторые – на x 2 = 1,100 м.

2. Установив угольник вертикально на опорной плоскости, измерить с его помощью

вертикальные координаты h и h ¢верхнего края шкалы, соответственно, в точках x = 0,220 м и x ¢ = 1,000 м (под ножками левой опоры должна лежать одна стандартная пластина). Значения координат занести в таблицу 3.1..

3. Включить воздушный насос (напряжение питания 4 В).

4. Нажать кнопку «механика: сброс». Тележку установить в крайнем левом положении и зафиксировать электромагнитом. С помощью пульта (кнопка «пуск») запустить движение тележки и зафиксировать промежутки времени t1 и t2 (см. пункт 6. упражнения 1.). Величины t 1 ,t 2 занести в таблицу 3.1.. Повторить еще четыре раза измерение t 1 ,t 2 и результаты также занести в таблицу

3.1..

Таблица 3.1.

h, мм	h ¢,мм	№ опыта	t1,с	t2,с

5. Последовательно увеличивая число пластин под ножками левой опоры до пяти, для каждого набора пластин выполнить пункты 2 – 4, занося результаты в таблицы 3.2. – 3.5., подобные таблице 3.1. Выключить насос.

Обработка результатов измерений.

Упражнение 1.

1. По измеренным величинам, представленным в таблице 2, рассчитать Y = 2 (x 2 - x 1) и

2 2

X = t 2 - t 1

занести их значения в таблицу 2.

2. Если тележка движется равноускоренно и ее начальная скорость равна нулю, то из формулы

(2) следует

() (2 2)

2 x 2 - x 1

= a t 2 - t 1

или Y = aX, (5)

где a величина ускорения тележки. Таким образом, теоретический график зависимости Y от X представляет собой прямую линию, проходящую через начало координат, а угловой коэффициент этой прямой равен ускорению тележки.

3. Нанести экспериментальные точки на диаграмму Y от X и провести через начало координат

 

«на глаз» наилучшую аппроксимирующую прямую Y %(X) так, чтобы она проходила как можно ближе ко всем экспериментальным точкам (см.

рис.3.). Выбрать на аппроксимирующей прямой

точку А, достаточно удаленную от начала

координат. По её координатам

X A и YA

вычислить ускорение как угловой коэффициент прямой Y %(X):

a гр =

Y

A. (6)

X A

РИС.3. Крестиками отмечены экспериментальные точки. Y %(X) – аппроксимирующая прямая.

N

Чем больше расстояние точки A от начала координат, тем меньше погрешность вычисления углового коэффициента прямой по формуле (6). Эта погрешность в дальнейшем не учитывается.

4. По отклонениям Yi - Y %(Xi) ординат

i

экспериментальных точек Yi от соответствующих ординат точек Y %(X) аппроксимирующей прямой рассчитать

погрешность ускорения:

(Y - Y (X))2

гр

D a =

a гр ×

å i % i

i =1

, (7)

YA N -1

где N = 5 – количество экспериментальных точек.

5. Записать доверительный интервал для ускорения: a = a гр ± D a гр.

Упражнение 2.

1. Для каждой серии измерений в таблицах 3.1 – 3.5 вычислить значение синуса угла наклона рельса к горизонту по формуле

h 0 - h -(h 0¢- h ¢)

sin a=

x ¢- x

. (8)

Результаты занести в таблицу 4.

Таблица 4.

Количество пластин	sin a	t 1, с	t 2, с	a, м с2

2. Для каждой серии измерений вычислить среднее значение времени t 1 по формуле

N

å t 1 i

t 1 =

i =1

N

, (9)

где N – количество измерений в серии.

Вычислить случайную погрешность по формуле

N

å(t 1 i

- t)2

D t = K (a

N) i =1

()

, (10)

1сл

S дов,

N N -1

где

KS (aдов, N) – коэффициент Стьюдента для доверительной вероятности aдов= 0,7 и

количества измерений N. Если результаты отдельных измерений в серии не отличаются друг от друга, то случайную погрешность можно положить равной нулю.

Найти полную погрешность по формуле

1 1сл

1пр

D t = (D t)2

+ (D t)2

, (11)

где D t 1пр

– приборная погрешность измерения t 1.

Доверительные интервалы

t 1 ± D t 1 занести в третий столбец таблицы 4.

3. По каждой серии измерений с помощью формул аналогичных формулам (9) – (11) найти

доверительные интервалы t 2 ± D t 2

таблицы 4.

для времени t 2 и результаты занести в четвертый столбец

4. Для каждой серии измерений вычислить значение ускорения и погрешности по формулам

2 (x 2 - x 1)

(D x

)2 + (D x)2

4 ((t 1D t 1)

+ (t 2D t 2))

a =;

2 1

D a a ×

2 = 1 +

2 1

((t 2)

2 2

- (t 1))

(12)

(t)2 - (t)2

(x - x)2

2 2 2

 

Найденные результаты в виде доверительных

интервалов a ± D a

таблицы 4.

занести в последний столбец

5. Пользуясь результатами из второго и пятого столбцов таблицы 4 нанести экспериментальные точки на диаграмму a от sin a. Показать погрешность найденных значений a на графике, изобразив доверительные интервалы для ускорения отрезками, параллельными оси a (см. рис. 4). Провести

аппроксимирующую прямую

a %(sina).

РИС.4.

6. Поскольку коэффициент трения m и угол a

достаточно малы, cos a в формуле (4) можно заменить единицей. С учетом этого теоретическая формула для ускорения имеет вид

a = g (sina -m). (14)

Следовательно, зависимость a от sin a является линейной, и угловой коэффициент этой зависимости равен ускорению свободного падения g.

7. Выбрать на аппроксимирующей прямой a %(sina) достаточно удаленные друг от друга точки А и В (см. рис. 4). По их координатам вычислить ускорение свободного падения как угловой коэффициент прямой:

g = aB - aA

. (15)

B A

гр sin a - sin a

8. По отклонениям ai - a %(sin a i) ординат экспериментальных точек от соответствующих ординат точек аппроксимирующей прямой рассчитать погрешность:

g гр

2 ((sin))2

D g гр

= ×

- 2

N

aB - aA

å

N

i =1

ai - a %

a i. (16)

9. Записать найденный доверительный интервал для ускорения свободного падения:

g = g гр ± D g гр.

Проверить попадает ли табличное значение в этот интервал.

Замечание. Угловые коэффициенты и их погрешности для аппроксимирующих прямых в упражнениях 1 и 2 можно рассчитать точнее по методу наименьших квадратов.

В соответствии с этим методом при обработке результатов в упражнении 1 необходимо использовать формулы

=

a гр

N

å X iYi

i =1

N

D a гр =

N

å (Yi - a гр X i)

i =1

N

, (17)

X

;

2

å

i i =1

(N -1)

X

å

i i =1

где

X i, Yi

– соответственно, абсциссы и ординаты экспериментальных точек на диаграмме Y от X.

При обработке результатов по методу наименьших квадратов в упражнении 2 следует применить формулы

N

é(sin a - sin a) a

(D a)2 ù

é(a - g

sin a - (A - g

sin a))2

(D a)2 ù

=

g гр

åë

i =1

N

i i i

2 2

û

; D g гр =

å i

i =1

N

гр i

N

гр i

û

2 2

, (18)

ë

û

åêé(sin a i - sin a) (D ai) úù

i =1

N N

(N - 2)åêé(sin a i -sin a) (D ai) úù

ë

i =1

ésin a

(D a)2 ù

é a (D a)2 ù

åë

где sin a= i =1

i i û

;

åë i i

A = i =1

û

; sin a, a, D a

– соответственно, абсциссы,

N

åé1 (D a)2 ù

N

åé1 (D a)2 ù

i i i

ë i û

i =1

ë i û

i =1

ординаты и погрешности ординат экспериментальных точек на диаграмме a от sin a.

Дата добавления: 2015-01-03