Функция выигрыша в матричных играх без седловой точки. Смешанные и оптимальные смешанные стратегии. Метод сведения решения матричных игр к задаче линейного программирования

Матричной называют антагонистическую (противоборство) парную игру с нулевой суммой (сумма выигрышей 2х игроков=0) что каждый игрок имеет конечное число чистых стратегий. Парная игра с нулевой суммой задается формально матрицей игры – матрицей А = { a_ij }, элементы которой определяют выигрыш первого игрока (и проигрыш второго), если первый игрок выберет i -ю (х) стратегию, а второй - j -ю (у) стратегию. Пара (i ₀, j ₀) называется седловой точкой матрицы (решением игры), если выполняются условия: 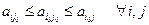(max по столбцу (I игрок), min по строке (II игрок)) или Седловой точкой функции f(x,y), опред-ной на множ-ве X (множ-во стратегий первого игрока) 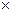Y(второго), наз-ся пара (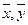) такая, что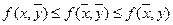

Значение функции выигрыша в седловой точке называется ценой игры.

Седловая точка обеспечивает равновесие в игре, но она существует не всегда (н-р, в 2-х пальцевой игре Морра ее нет).

Задача Морра: каждый из 2-х игроков в одно и тоже время показывает 1 или 2 пальца и произносит цифру вслух, пытаясь тем самым угадать сколько пальцев покажет противник. В случае угадывания игрок получает кол-во очков равное сумме пальцев. (сказал, показал)

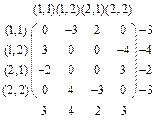
по Теореме о седловой точке: для того чтобы функция f(x,y) имела седловую точку необх и дост, чтобы выполнялось рав-во 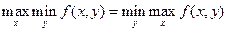. Здесь -2 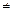2, т.е. седловой точки нет.

В дан. случае игрокам не выгодно пользоваться одной и той же стратегией, так как в этом случае противник будет выбирать наилучший для себя вариант. Тогда выбор стратегий должен быть вероятностным – выбор осуществляется случайным образом с определенными вероятностями.

Если обозначить через 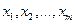вероятности выбора i -ой стратегии первым игроком. При этом:

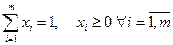Сумма=1, т.к. он обязан что-то выбрать.

А через 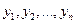вероятности выбора j -ой стратегии вторым игроком:

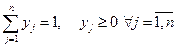
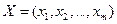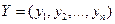то наборы и называются смешанными стратегиями первого и второго игроков соответственно. Смешанная стратегия – это набор вероятностей чистых стратегий.

Тогда выигрыш первого игрока при условии, что он выбирает i -ю стратегию, а второй – j -ю стратегию составит .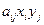

Функция выигрыша первого игрока 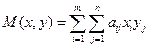– мат. ожидание выигрыша первого игрока. Соответственно средний выигрыш второго игрока = – M (x, y)

Любая матричная игра имеет решение в смешанных стратегиях, т.е. существует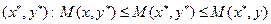

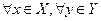
Решение задачи (нахождение оптимальных смешанных стратегий) заключается в нахождении седловой точки функции M (x, y) на множестве 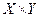. Оптимальность понимается в том смысле, что набор устраивает игроков, никто не хочет выбирать другие стратегии.

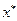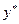Тогда и называются оптимальными смешанными стратегиями игроков. Задачи заключается в нахождении оптимальных смешанных стратегий игроков и цены игры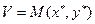

Т. [о необходимых и достаточных условиях оптимальности смешанных стратегий] Пусть игра определена матрицей 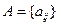и ценой игры V. Для того, чтобы смешанная стратегия 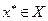была оптимальной стратегией 1-го игрока 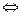выполнение следующего неравенства:

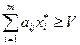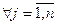, (1)

Для того, чтобы смешанная стратегия 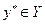была оптимальной стратегией 2-го игрока 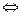выполнение следующего неравенства:

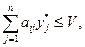
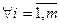(2).

СЛЕДСТВИЕ: Если для смешанных стратегий (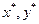) и числа V одновременно выполняются (1) и (2), то (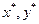) будут оптимальными стратегиями игроков, а V – цена игры.

Метод сведения решения матричных игр к задаче линейного программи­рования. (II метод)

Пусть игра определена матрицей 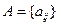и ценой игры V. Из теоремы об оптимальности смешанных стратегий: для оптим.смешан.стратегий должно вып-ся двойное нерав-во: (*)

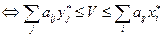1) Рассмотрим левую часть:

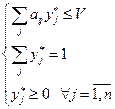
Решение СЛАУ сводится к задаче ЛП.

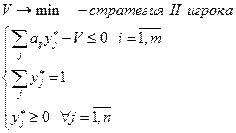(1)

2) Рассмотрим правую часть (аналогично):

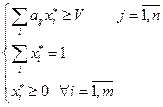
V меняем на W, так как системы (1)-(2) независимы, поэтому они имеют разные переменные.

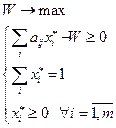(2)

Допустим, решили задачи и получили:

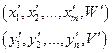
Если в этих решениях последние координаты совпадали бы, то выполнялись бы неравенства:

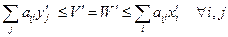
Тогда для каких-то 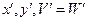выполнялось бы следствие теоремы оптимальности.

Покажем двойственность.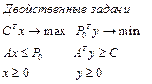

Обозначим

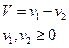
{неравенства (3)-(4) лучше написать в развернутом виде, чтобы была видна двойственность}

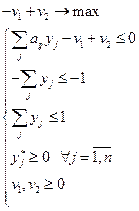
(3)

ЗАМ: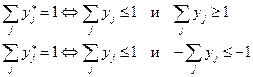

Аналогично для второй задачи:

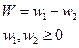
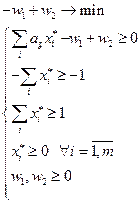(4)

Задачи (3) и (4) – двойственные, т.е. решение одной можно найти из решения другой (в последней симплекс-таблице в строке оценок на местах, соответствующих дополнительным переменным). Значения линейных форм в оптимальной точке совпадут. Поэтому, получив решения 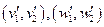, получим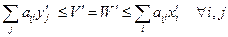

Алгоритм решения:

4. по матрице А построить задачи (3) и (4)

5. найти решения задач

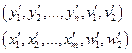
тогда 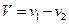– цена игры, оптимальные стратегии игроков:

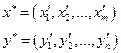
Преимущества и недостатки метода:

+ сразу получаем решение игры, т.е. не надо переобозначать

+ можно решать игры с любой ценой игры

– больше на 2 переменные

– надо вводить дополнительные переменные, так как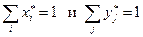

Дата добавления: 2015-01-03