Основные определения выпуклого программирования

Методы наискорейшего и координатного спуска для минимизации выпуклой функции без ограничений. Их алгоритмы и геометрическая интерпретация

Предположим, что имеется функция многих переменных .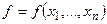

Производной вектора 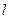в точке х называется следующий предел: .

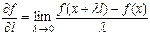Абсолютная величина производной по направлению есть скорость изменения функции в этом направлении, а знак показывает либо возрастание, либо убывание.

Градиентом функции 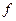называется следующий вектор:

Направление градиента есть направление наискорейшего возрастания функции.

Производная функции по направлению градиента есть модуль (длина)градиента.

Градиент функции направлен по нормали к линии уровня.

Множество Х называется выпуклым, если вместе с любыми двумя точками 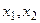содержит также их выпуклую линейную комбинацию:

Функция 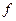, определенная на выпуклом множестве Х, называется выпуклой, если для любых точек 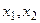из множества Х и выполняется следующее неравенство:

Функция 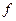, определенная на выпуклом множестве Х, называется вогнутой, если для любых точек 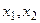из множества Х и выполняется следующее неравенство:

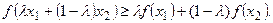
Выпуклая функция не может принимать больших значений, чем прямая, соединяющая любые две точки (если есть касательная, то она лежит выше касательной).

Вогнутая функция не может принимать меньших значений, чем прямая, соединяющая любые две точки (если есть касательная, то она лежит ниже касательной).

Свойства:

1) Если функция 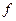дифференцируема во внутренних точках множества Х, то для любых внутренних точек 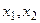справедливо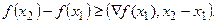

2) Выпуклая функция, определенная на выпуклом множестве, достигает своего глобального минимума в точке, в которой градиент обращается в ноль.

Дата добавления: 2015-01-03