Пряма і обернена задачі теорії похибок

Основи теорії похибок, класифікація похибок, джерела похибок

Під похибкою будемо розуміти величину, що характеризує точність результату. Похибки, що виникають при розв’язуванні задачі, можна поділити на три групи:

1. неусувна похибка

2. похибка методу

3. похибка обчислень

Неусувна похибка є наслідком: а)неточності вхідних даних, що входять до математичного описання задачі, б)невідповідності математичної моделі реальній задачі (інколи цю похибку називають похибкою математичної моделі). Похибка методу пояснюється тим, що для розв’язування математичної задачі доводиться використовувати наближені методи, оскільки отримання точного розв’язку необмеженої або неприйнятно великої кількості арифметичних операцій, а в багатьох випадках і просто неможливо. Похибка обчислень виникає при вводі-виводі даних до ПЕОМ та при виконанні математичних операцій. Основна задача теорії похибок – знаходження області невизначеності результату. Розглянемо процес заокруглення чисел. Якщо число x=4,167493 і його потрібно заокруглити до п’яти десяткових знаків після коми, то будемо мати x*=4,16749. Тобто, якщо старший розряд, що відкидається менше 5, то попередня цифра не змінюється. Якщо x=4,167493 потрібно заокруглити до чотирьох знаків після коми, то x*=4,1675. Тобто, якщо старший розряд, що відкидається дорівнює, або більше 5, то попередня цифра в числі збільшується на 1. Під помилкою чи похибкою Da наближеного числа a загалом розуміють різницю між відповідним точним числом та даним наближеним числом: Da = A – a Якщо A > a, то Da > 0, якщо A < a, то Da < 0. У багатьох випадках знак помилки невідомий, тому вводиться поняття абсолютної похибки та граничної абсолютної похибки. Абсолютною похибкою D наближеного числа a називається абсолютна величина різниці між відповідним точним числом A та числом a: D = |A - a|. Граничною абсолютною похибкою Da наближеного числа називається число, не менше абсолютної похибки цього числа. Таким чином, якщо Da - гранична абсолютна похибка наближеного числа a, яке замінює точне A, то D = |A - a| £ Da.

Під похибкою будемо розуміти величину, що характеризує точність результату. Похибки, що виникають при розв’язуванні задачі, можна поділити на три групи:

1. неусувна похибка

2. похибка методу

3. похибка обчислень

Основна задача теорії похибок – знаходження області невизначеності результату. Розглянемо процес заокруглення чисел. Якщо число x=4,167493 і його потрібно заокруглити до п’яти десяткових знаків після коми, то будемо мати x*=4,16749. Тобто, якщо старший розряд, що відкидається менше 5, то попередня цифра не змінюється. Якщо x=4,167493 потрібно заокруглити до чотирьох знаків після коми, то x*=4,1675. Тобто, якщо старший розряд, що відкидається дорівнює, або більше 5, то попередня цифра в числі збільшується на 1. Під помилкою чи похибкою Da наближеного числа a загалом розуміють різницю між відповідним точним числом та даним наближеним числом: Da = A – a Якщо A > a, то Da > 0, якщо A < a, то Da < 0. У багатьох випадках знак помилки невідомий, тому вводиться поняття абсолютної похибки та граничної абсолютної похибки. Абсолютною похибкою D наближеного числа a називається абсолютна величина різниці між відповідним точним числом A та числом a: D = |A - a|. Граничною абсолютною похибкою Da наближеного числа називається число, не менше абсолютної похибки цього числа. Таким чином, якщо Da - гранична абсолютна похибка наближеного числа a, яке замінює точне A, то D = |A - a| £ Da. Обернена задача теорії похибок полягає в наступному: з якою точністю потрібно задати значення аргументів 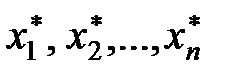функція 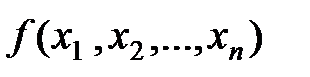, щоб похибка значення функції 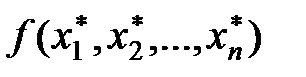не перевищувала заданої величини ε.

Для функції однієї змінної y=f(x) абсолютну похибку можна наближено обчислити за формулою

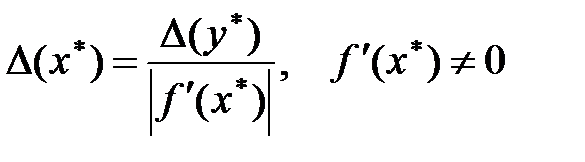. Для функції декількох змінних 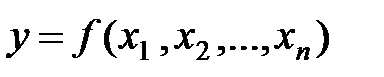задача розв’язується за допомогою наступних рекомендацій:

а)Принцип рівних впливів, тобто вважаємо, що всі доданки 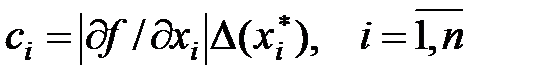рівні між собою. Тоді абсолютні похибки всіх аргументів визначаються формулою

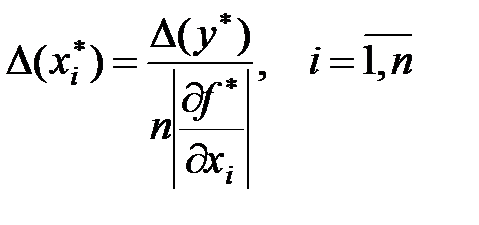; б)Вважаємо всі похибки рівними, причому максимально можливими, тобто покладемо

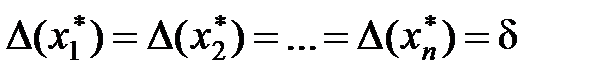, де .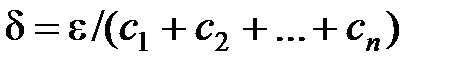

Дата добавления: 2015-01-03