Інтерполювання у випадку рівновіддаленихвузлів: друга інтеполяційна формула Ньютона

Первая интерполяционная формула Ньютона для x, расположенных далеко от 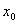, даёт малую точность. В этом случае обычно применяется вторая интерполяционная формула Ньютона.

Пусть имеем систему значений для равноотстоящих значений независимой переменной 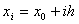, 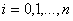. Построим интерполяционный полином следующего вида:

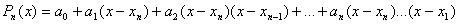. (4.20)

Используя обобщённую степень выражение (4.20) запишем так:

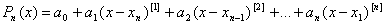. (4.21)

Задача состоит в определении коэффициентов , ,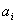

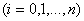таким образом, чтобы были выполнены равенства (4.13). Для этого необходимо и достаточно, чтобы

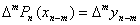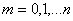, . (4.22)

Положим 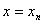в формуле (4.21). Тогда будем иметь:

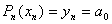. Далее берём от левой и правой части формулы (4.21) конечные разности первого порядка

.

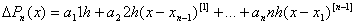В последнем выражении, полагая и учитывая соотношение (4.22), будем иметь: 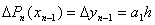. Следовательно 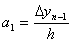. Аналогично составим вторую разность от 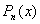, получим:

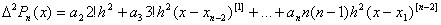
Полагая 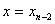, находим 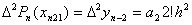. Таким образом, . Характер закономерности коэффициентов 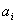достаточно ясен. Применяя метод математической индукции, можно строго доказать, что

, .

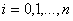Подставляя эти значения в формулу (4.20), будем иметь окончательно:

.(4.23)

Формула (4.23) носит название второй интерполяционной формулы Ньютона. Введём более удобную запись формулы (4.23). Пусть , тогда 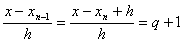, , 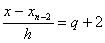и т.д. Подставляя эти выражения в формулу (4.23), получаем

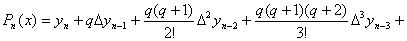
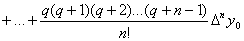, (4.24)

Вторая формула Ньютона используется для интерполирования функции в окрестности . Погрешность второй интерполяционной формулы Ньютона имеет вид:

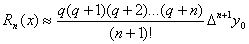. (4.25)

Замечание. Как первая, так и вторая интерполяционные формулы Ньютона могут быть использованы для экстраполирования функции, т.е. для нахождения значений функции для значений аргументов x, лежащих вне пределов таблицы. Ниже приводится схема использования формул.

13.Інтерполяційний поліном Лагранжа. Побудова полінома Лагранжа для функції, значення якої подано таблицею

Для построения интерполяционного многочлена прямым методом необходимо предварительно решить систему линейных уравнений (2.16). Интерполяционная формула Лагранжа не требует решения системы уравнений (2.16). В общем виде полином Лагранжа можно представить формулой:

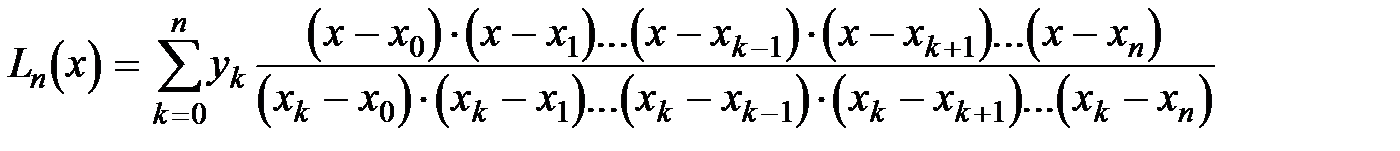(2.17)

где - узлы интерполяционной сетки, - значения функции 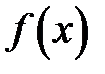в узловых точках.

Каждый из слагаемых формулы (2.17), как нетрудно убедиться, является полиномом степени n, следовательно 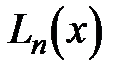- также есть полином n-ой степени (как сумма многочленов n-ой степени). Структура формулы (2.17) построена таким образом, чтобы выполнялось условие , в чем нетрудно убедиться.

Если функция 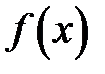достаточно гладкая, т.е. имеет непрерывные производные вплоть до (n+1)- порядка включительно, то погрешность интерполяции (остаточный член), определяемую формулой

,

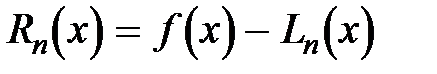можно оценить следующим образом:

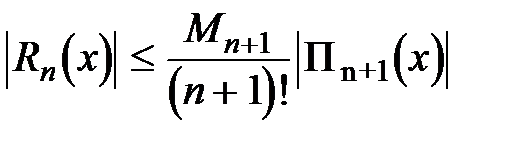, (2.18)

где

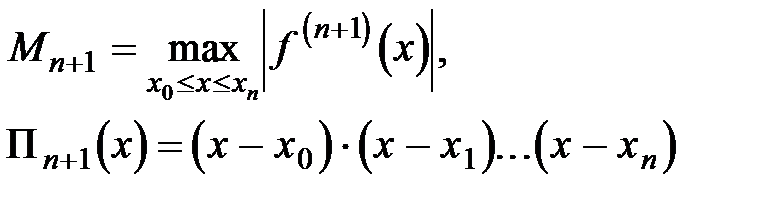
Полином Лагранжа полезен тем, что в явном виде содержит значение функции .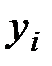

Дата добавления: 2015-01-03