
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратурні формули з рівновіддаленими вузлами: формула Ньютона
|
|
|
|
Пусть имеем функцию f(x), заданную в равноотстоящих точкая xi отрезка [a,b], с помощью значений yi=f(xi). Для нахождения производных y'(x)=f'(x), y''(x)=f''(x) и т.д., функцию y приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов x0, x1,..., xk(k≤n).
Имеем
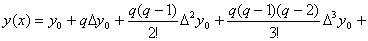
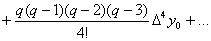 ,
,
где 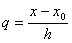 , h=xi+1-xi.
, h=xi+1-xi.
Производя перемножение биномов, получим:

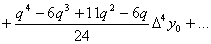 .
.
Так как 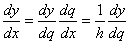 , то
, то
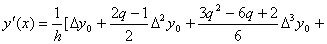
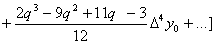 .
.
Аналогично, так как 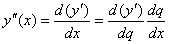 .
.
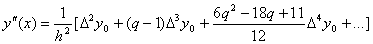 .
.
Таким же способом в случае необходимости можно найти производные любого порядка. Заметим, что при нахождении производных в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента. Иногда требуется находить производные функции y в основных табличных точках, т.е. в узлах 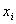 . В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, получаем q=0. Тогда будем иметь:
. В этом случае формулы численного дифференцирования упрощаются. Так как каждое табличное значение можно считать за начальное, то положим x=x0, получаем q=0. Тогда будем иметь:
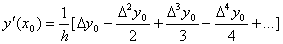 .
.
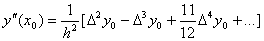 .
.
Если Pn(x) - интерполяционный полином Ньютона, содержащий конечные разности до n - го порядка включительно, то его погрешность выражается формулой:
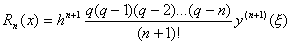 .
.
Находим погрешность формулы:

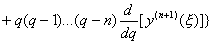 .
.
Полагая в (5.9) x=x0 и учитывая, что q=0 и  , будем иметь
, будем иметь
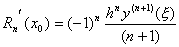 .
.
Так как  , то
, то
 .
.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 466; Нарушение авторских прав?; Мы поможем в написании вашей работы!