
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поліноми Ньютона. Залишковий член формули Ньютона. Точність інтерполяції
|
|
|
|
Інтерполяційний поліном Ньютона
Нехайf(x) - функція; (0)
- поділена різниця; (1)
- друга поділена різниця; (2)
f(x) = f(x0) + (x - x0) f(x, x0);
f(x, x0) = f(x0, x1) + (x - x1) f(x, x0, x1);
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x, x0, x1);
Аналогічно:
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x, x0, x1) + (x - x0) (x - x1) (x - x2) f(x, x0, x1, x2);
…
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x0, x1, x2) + (x - x0) (x - x1) (x - x2) f(x0, x1, x2, x3) + … + (x - x0) (x - x1)… (x - xn-1) f(x0, x1,…, xn) + (x - x0) (x - x1)… (x - xn) f(x, x0,…, xn),(3)
причому підкреслена частина є деяким поліномом n-го порядку:
f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x0, x1, x2) + (x - x0) (x - x1) (x - x2) f(x0, x1, x2, x3) + (x - x0) (x - x1)… (x - xn-1) f(x0, x1,…, xn) = Pn(x).
Якщо x = x0, x1, …, xn, то f(xi) = Pn(xi) = yi, тому що (x - x0) … (x - xn) f(x, x0, …, xn) = 0!
Права частина виразу (3) і є інтерполяційним поліномом Ньютона.
Якщо x0 < x1 < … < xn, то це – формула інтерполяції вперед, якщо навпаки –назад.
Точність інтерполяції
График интерполяционного полинома у = (х) проходит через заданные точки, т. е., значения полинома (х) и данной функции у = (х) совпадают в узлах х = хi (i = , ,..,. n). Если функция (х) сама является полиномом степени n, то имеет место тождественное равенство (х) = (х). В общем случае в точках, отличных от узлов интерполяции
R(x) = (х) - (х).
Эта разность и есть погрешность интерполяции, и называется остаточным членом интерполяционной формулы. Оценим его значение.
Предположим, что заданные числа yi являются значениями некоторой функции y = (х) в точках х = хi. Пусть эта функция непрерывна и имеет непрерывные производные до n + 1 порядка включительно. Можно показать, что в этом случае остаточный член интерполяционного полинома Лагранжа имеет вид:
RL (x) = 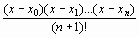 (n+)()
(n+)()
где (n+) () - производная (n+)-го порядка функции (х) в некоторой точке х = , [x, xn]. Если максимальное значение этой производной равно:
Mn + = 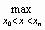 (n+) (x),
(n+) (x),
то можно записать формулу для оценки остаточного члена интерполяционного полинома Лагранжа
RL (x) 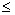 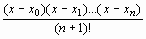 Mn+ Mn+
| (17) |
Остаточный член первой интерполяционной формулы Ньютона можно записать в виде:
RP (x) = 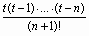 (n+) () h n + ,
(n+) () h n + , 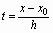 . (18)
. (18)
Остаточный член второй интерполяционной формулы Ньютона:
RP (x) = 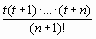 (n+) () h n + ,
(n+) () h n + , 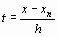 . (19)
. (19)
Если предположить, что разности n + уn почти постоянны для функции y = f(x) и h достаточно мало, и учитывая, что
(n+) (х) =  ,
,
приближенно можно положить:
(n+) () 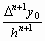 .
.
В этом случае можно записать следующую формулу остаточного члена первой интерполяционной формулы Ньютона:
RP (x) 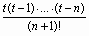 n+у.
n+у.
Формула остаточного члена второй интерполяционной формулы Ньютона имеет вид:
RP (x) 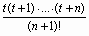 n+уn.
n+уn.
24.Задача Коші для звичайних диференціальних рівнянь
Задача Коші - одна з основних задач теорії диференціальних рівнянь полягає в пошуку розв'язку (інтеграла) диференціального рівняння, що задовольняє початковим умовам (початковим даним). Задача Коші зазвичай виникає при аналізі процесів, обумовлених диференціальним законом і початковим станом, математичним виразом яких і є рівняння та початкова умова (звідси й термінологія та вибір позначень: початкові дані задаються при t = 0, а розв'язок знаходиться при t > 0). Від крайових задач задача Коші відрізняється тим, що область, в якій повинен бути визначений шуканий розв'язок, тут заздалегідь не вказується. Проте, задачу Коші можна розглядати як одну з крайових задач. Основні питання, що позв'язані з задачею Коші, такі:
Чи існує (хоч би локально) розв'язок задачі Коші?
Якщо розв'язок існує, то яка область його існування?
Чи існує єдиний розв'язок?
Якщо розв'язок єдиний, то чи буде він коректним, тобто неперервним (в якому-небудь змісті) щодо початкових даних?
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 964; Нарушение авторских прав?; Мы поможем в написании вашей работы!