Використання рядів Тейлора. Оцінка похибки при використанні рядів Тейлора

Використання рядів Тейлора. Оцінка похибки при використанні рядів Тейлора

Задача численного дифференцирования состоит в приближенном вычислении производных функции f(x) по заданным в конечном числе точек значениям этой функции.

Один из универсальных способов построения формул численного дифференцирования состоит в том, что по значениям функции f(x) в некоторых узлах x0, x1,..., xN строят интерполяционный полином PN(x) (обычно в форме Лагранжа) и приближенно полагают f(r)(x)»P(r)N(x), 0 ≤ r ≤ N (4.1)

В ряде случаев наряду с приближенным равенством удается (например, используя формулу Тейлора) получить точное равенство, содержащее остаточный член R (погрешность численного дифференцирования):

f(r)(x) = P(r)N(x) + R, 0 ≤ r ≤ N

Такие формулы называются формулами численного дифференцирования с остаточными членами. Формулы с отброшенными остаточными членами называются просто формулами численного дифференцирования.

Ниже приводятся несколько распространенных формул численного дифференцирования с остаточными членами для первой (r=1) и второй (r=2) производных в узлах, расположенных с постоянным шагом hiºh > 0 [6, стр.58]:

r=1, N=1 (два узла): f '(x0) = (f1 - f0)/h - hf ''(x)/2 (4.2)

f '(x1) = (f1 - f0)/h + hf ''(x)/2 (4.3)

r=1, N=2 (три узла): f '(x0) = (-3f0 + 4f1 - f2)/2h + h2f '''(x)/3 (4.4)

f '(x1) = (f2 - f0)/2h - h2f '''(x)/6 (4.5)

f '(x2) = (f0 - 4f1 + 3f2)/2h + h2f '''(x)/3 (4.6)

r=2, N=2 (три узла): f ''(x0) = (f0 - 2f1 + f2)/h2 - hf '''(x) (4.7)

f ''(x1) = (f0 - 2f1 + f2)/h2 - h2f (4)(x)/12 (4.8)

f ''(x2) = (f0 - 2f1 + f2)/h2 + hf '''(x) (4.9)

r=2, N=3 (четыре узла): f ''(x0) = (2f0 - 5f1 + 4f2 - f3)/h2 + 11h2f (4)(x)/12 (4.10)

f ''(x1) = (f0 - 2f1 + f2)/h2 - h2f (4)(x)/12 (4.11)

f ''(x2) = (f0 - 2f1 + f3)/h2 - h2f (4)(x)/12 (4.12)

f ''(x3) = (-f0 + 4f1 - 5f2 + 2f3)/h2 + 11h2f (4)(x)/12 (4.13)

Наиболее простым и достаточно эффективным способом приближения функций является использование формулы Тейлора для разложения функций в степенной ряд.

Пусть задана непрерывная функция , имеющая непрерывные производные до порядка включительно. Из математического анализа известно, что такую функцию можно разложить в окрестностях точки по степеням в ряд Тейлора:

, (2.1)

где - ошибка ограничения, связанная с заменой при вычислении бесконечного степенного ряда, первыми его n членами. Ошибку ограничения можно оценить по формуле:

. (2.2)

где x находится между и .

Формула Тейлора не только дает возможность организовать численный метод вычисления значений функции , но и оценить величину ошибки ограничения по формуле (2.2). При ее использовании от вычислителя требуется определить точку , в окрестностях которой будет производиться разложение функции. При выборе 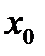следует руководствоваться соображениями точности представления коэффициентов ряда (2.1) и величиной рабочего диапазона, внутри которого будут производиться вычисления.

Дата добавления: 2015-01-03