Порядковая функция графа

ТЕМА 2-2.

Методы оптимизации на графах.

Методы оптимизации находят широкое применение при проектировании сложных систем обработки и передачи информации, в частности: вычислительных систем и сетей, сетей передачи и распределения электроэнергии, товаров и т.д.

Их применение связано с поиском оптимальных решений по эффективному использованию имеющихся технических и программных средств системы.

Методы оптимизации в значительной степени базируются на теории графов и комбинаторном анализе.

Методы оптимизации базируются на ряде дополнительных понятий теории графов: порядковой функции графа, числовых функциях графа. Рассмотрим их подробнее.

Пусть задан граф G=(X,s), а N₀, N₁,..., N_r - такие подмножества, что:

N₀={x_i/x_i Î X, s ^(-1)_xi=Æ}

N₁={x_i/x_i Î X-N₀, s ^(-1)_xiÌ N₀}

N₂={x_i/x_i Î X-(N₀ È N₁), s ^(-1)_xiÌ (N₀ È N₁)}

.......................................................

N_r={x_i/x_i Î X- 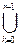N_k, s ^(-1)_xiÌ 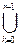N_k }

Суть задания множеств N₀, N₁,..., N_r: в множество N₀ ни одна дуга не входит. В любое из оставшихся множеств могут входить дуги только из множеств, номера индексов которых меньше номера индекса рассматриваемого множества. Сказанное даёт возможность разбить всё множество вершин графа Х на (r +1) ярусов со связями между ярусами по типу "с предыдущего в последующие".

Графически множества N₀, N₁,..., N_r могут быть проиллюстрированы так:

Функция О(х), определяемая равенством

(x_iÎN_k)Þ (O(x_i)=k)

называется порядковой функцией графа без контуров.

Пример. Задан граф G.

Множество Х, можно, например, разбить на подмножества N₀, N₁,..., N₃, т.е. задать порядковую функцию следующим образом:

Подмножества N₀, N₁,..., N_r называются обычно уровнями.

Рассмотрим алгоритм нахождения уровней графа:

1. Задать граф матрицей смежности.

2. Образовать дополнительную к матрице смежности строку l₀, в каждой её клетке записать число единиц по соответствующему столбцу матрицы смежности. Вершины графа, соответствующие нулевым клеткам строки l₀, образуют подмножество N₀.

3. Вычеркнуть из матрицы смежности строки, соответствующие вершинам графа, вошедшим в N₀.

4. Образовать дополнительную строку l₁, заменив в ней нулевые клетки строки l₀ крестиками. В остальные клетки строки l₁ вписать число единиц по соответствующему столбцу матрицы смежности графа. Вершины графа, соответствующие нулевым клеткам строки l₁, образуют подмножество N₁.

5. Процесс образования дополнительных строк l_i прекратить, когда все строки матрицы смежности будут вычеркнуты.

Пример. Задан граф G (из предыдущего примера).

l0

N₀={1}

l1

Х

N₁={2,3,4}

l2

Х

Х

Х

Х

N₂={5,6}

l3

Х

Х

Х

Х

Х

Х

N₃={7}

Примечание: если граф содержит контур, то обязательно появится строка без нулей. Поэтому предложенный алгоритм даёт возможность установить наличие контуров в графе. Петля также определяется как контур.

Дата добавления: 2015-01-03