Алгоритм Флетчера-Кларка

Эвристические методы оптимизации.

Пример.

Найти минимальный путь из x₀ в x₆.

1 шаг. Вершине x₀ приписывается метка l₀ =0. Всем остальным x_i приписывается l_i=¥.

2 шаг. Рассматриваем вершину x₁ и дугу x₀®x₁. Вершине x₁ приписываем метку l₁¢=l₀+l(x₀,x₁) =0+4=4.

3 шаг. Рассматриваем вершину x₃ и дугу x₀®x₃. Тогда l₃¢=l₀+l(x₀,x₃) =0+2=2.

4 шаг. Рассматриваем вершину x₂ и дугу x₀®x₂. Тогда l₂¢=l₀+l(x₀,x₂) =0+5=5.

5 шаг. Рассматриваем вершину x₅ и дугу x₀®x₅. Тогда l₅¢=l₀+l(x₀,x₅) =0+4=4.

6 шаг. Рассматриваем вершину x₄ и дугу x₁®x₄. Тогда l₄¢=l₁+l(x₁,x₄) =4+2=6.

7 шаг. Рассматриваем вершину x₆ и дугу x₄®x₆. Тогда l₆¢=l₄+l(x₄,x₆) =6+1=7.

Разметка вершин показана на рисунке кружками. Выбор дуги (x_i,x_j) при разметке вершины x_j осуществляется совершенно произвольно. Единственное ограничение: метка l_i вершины x_i не должна быть равна ¥.

8 шаг. Рассматриваем вершину x₂ и стремимся уменьшить её метку. Для этого рассматриваем все дуги, ведущие в x₂: выписываем все возможные выражения для метки l₂¢: l₂¢=l₀+l(x₀,x₂) =0+5=5.

l₂¢=l₃+l(x₃,x₂) =2+1=3.

l₂¢= min = 3, поэтому заменяем метку вершины x₂ на 3.

9 шаг. Аналогично для x₄: l₄¢=l₁+l(x₁,x₄) =4+2=6.

l₄¢=l₂+l(x₂,x₄) =3+2=5.

l₄¢= min = 5, поэтому заменяем метку вершины x₄ на 5.

10 шаг. Аналогично для x₅: l₅¢=l₃+l(x₃,x₅) =2+1=3.

l₅¢=l₄+l(x₄,x₅) =5+2=7.

l₅¢= min = 3, поэтому заменяем метку вершины x₅ на 3.

11 шаг. Аналогично для x₆: l₆¢=l₄+l(x₄,x₆) =5+1=6.

l₆¢=l₂+l(x₂,x₆) =3+3=6.

l₆¢=l₅+l(x₅,x₆) =3+5=8.

l₆¢= min = 6, поэтому заменяем метку вершины x₆ на 6.

12 шаг. Для x₁ понижение невозможно.

Дальнейшее понижение меток вершин невозможно, поэтому прекращаем разметку.

13 шаг. Ищем минимальный путь из x₆ в x₀.

(x₆ , x₄, x₂, x₃, x₀) длина пути: 2+1+2+1=6

(x₆ , x₂, x₃, x₀) длина пути: 3+2+1=6

Пример для самостоятельной работы:

На практике иногда нужно найти оптимальное решение задачи, для которой метод оптимизации неизвестен.

В этом случае могут быть использованы эвристические методы. Такие методы могут не дать оптимального решения, но позволяют получить достаточно хороший практический результат.

В качестве примера будем рассматривать эвристический метод для задачи о перевозках, которая называется задачей Флетчера-Кларка.

Общая постановка задачи:

Предприятие Р₀ снабжает n складов: Р₁, Р₂, Р₃,....Р_n. Количество машин, используемых для перевозки, не ограничено. Все машины имеют одинаковую грузоподъёмность, для каждой машины она равна С.

Стоимость перевозки между P_i и P_j равна d_ij ¹ d_ji.

Каждая отправляемая с предприятия Р₀ машина должна вернуться обратно.

Вместимость склада P_i равна С_i.

При какой минимальной общей стоимости перевозок можно заполнить все склады при условии, что маршруты перевозок представляют собой контуры, попарно пересекающиеся только в точке Р₀?

Примечание: можно рассматривать различные обобщения этой задачи, вводя дополнительные ограничения на грузоподъёмность, проходимость дорог, количество заездов на один склад.

Работу метода рассмотрим на примере: задача о перевозках задана таблицами вместимости складов С_i и стоимости перевозок d_ij. Для удобства на рисунке они совмещены.

Ci		P0	P1	P2	P3	P4	P5	P6
¥	P0
	P1
	P2
	P3
	P4
	P5
	P6

C =10 - вместимость одной машины.

В каждой клетке на пересечении P_i и P_j указана стоимость перевозки d_ij.

На рисунке приведено одно из возможных решений:

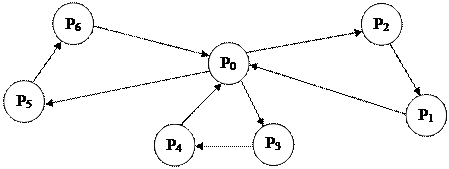С₆=2 С₂=6

С₅=8 С₁=4

С₄=1 С₃=3

Такие перевозки возможны, так как вместимость складов в контурах не превышает 10.

Значение стоимости перевозок по каждому из контуров рисунка:

(Р₀,Р₂,Р₁,Р₀)= d₀₂ + d₂₁ + d₁₀ =6+3+4=13;

(Р₀,Р₃,Р₄,Р₀)= d₀₃ + d₃₄ + d₄₀ =8+8+2=18;

(Р₀,Р₅,Р₆,Р₀)= d₀₅ + d₅₆ + d₆₀ =4+4+5=13;

Общая стоимость перевозок: 13+18+13=44.

Рассмотрим теперь метод Флетчера-Кларка.

Алгоритм:

1. Для каждой пары вершин (P_i, P_j), таких, что i¹j, i¹0, j¹0 определить параметр l_ij= d_i0 + d_0j - d_ij и занести его в таблицу.

2. В качестве начального решения выбрать тривиальное решение S вида S={(P₀,P₁,P₀,), (P₀,P₂,P₀,),........, (P₀,P_п,P₀,)}.

3. Для каждого маршрута в найденном решении S вычислить значение параметров g _i, i ¹0 по формуле:

g _i= 0, если (P_i, P₀) Ï S

1, если (P_i, P₀) Î S

4. Все вершины P_m1, P_m2,......., P_mk каждого маршрута из S (исключая P₀) объединяются в класс { P_m1, P_m2,......., P_mk } и вычисляется объёмность перевозки

Q { P_m1, P_m2,......., P_mk }= C_m1 + C_m2 +.......+ C_mk,

где C_mi вместимость склада P_mi.

5. Выбрать в таблице значений l_ij величину l_ij = maximum > 0 (если таких величин несколько, то выбрать любую). Если для выбранной величины l_ij склады P_i и P_j принадлежат разным классам, то объединить эти классы в один при выполнении условий:

а). g _i =g _j =1

б). Q { P_i, P_l, P_k.,......... } + Q { P_j, P_m,. P_v.,.....} £ C,

выделив l_ij в таблице меткой

Если одно из условий а) или б) не выполняется, то зачеркнуть клетку l_ij в таблице

6. Найти новое значение g _i, i ¹0.

7. Повторять пункты 4 и 5 до тех пор, пока есть возможность выбора величины l_ij > 0

Дата добавления: 2015-01-03