
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство
|
|
|
|
Зашифуем каждую комбинацию с помощью нулей и единиц: для каждого типа напишем столько единиц, сколько предметов этого типа входит в комбинацию, а предметы различных типов отделить нулями. При этом число единиц будет k, а число нулей – n–1. Различным комбинациям будут соответствовать различные перестановки с повторениями из k элементов первого вида и n–1 элементов второго вида, а каждой перестановке с повторениями – своя комбинация. Итак, 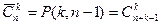 .
.
Встречаются задачи, в которых на сочетания с повторениями накладывается дополнительное условие, например, когда в комбинацию обязательно должны входить элементы r фиксированных типов, где r≤n. Эта задача легко сводится к уже решенной. Для того чтобы обеспечить присутствие заданных r типов, возьмем с самого начала по одному элементу каждого такого типа. Тем самым в k-сочетании окажутся заняты r мест. Поэтому ответом на задачу будет число 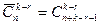 . В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится
. В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится 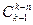 .
.
Задача.
Сколько существует различных бросаний двух одинаковых кубиков?
Решение.
Переформулируем задачу. Всего при подбрасывании одного кубика возможны шесть ситуаций – имеем предметы шести различных типов. Подбрасывают два кубика, следовательно, из данных шести типов предметов необходимо выбрать два, причем нас не интересует порядок выбора, и допускается выбор одинаковых предметов. Таким образом, это задача на сочетания с повторением. По формуле для вычисления количества сочетаний с повторением имеем 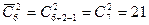 различных бросаний двух одинаковых кубиков.
различных бросаний двух одинаковых кубиков.
Комбинаторика разбиений
Многим комбинаторным задачам можно придать вид стандартной схемы. В этой схеме объекты (предметы) помещаются в ящики. Из-за наложения различных ограничений получаются различные задачи. Рассмотрим некоторые из них.
Имеется n1 предметов одного сорта, n2 – другого,..., nk – k-го сорта. Сколькими способами можно разложить их в два ящика?
Так как в каждый ящик может попасть от 0 до ni предметов i-го сорта (во второй все оставшиеся), по правилу произведения получаем (n1+1)∙(n2+1)∙...∙(nk+1) способов раскладки.
Задача.
Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они могут разделить эти цветы?
Решение.
Необходимо 10 предметов одного вида, 15 – второго и 14 – третьего разложить в два ящика. Применяя рассуждения, аналогичные приведенным выше, получаем 11×16×15=2460 способов раздела цветов.
Следствие 1. Если все предметы различны (n1=n2=...=nk=1), то их можно разложить 2k способами.
Следствие 2. Если в каждый ящик нужно положить не менее si предметов i-го сорта, то получим формулу: (n1-2s1+1) × (n2-2s2+1) ×...× (nk-2sk+1).
Даны n различных предметов и k ящиков. Надо положить в первый ящик n1 предметов, во второй – n2,..., в k-ый – nk, где n1+...+nk=n. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике?
Выложим все предметы в один ряд. Это можно сделать n! способами. Первые n1 предметов положим в первый ящик, вторые n2 предмета – во второй ящик, …, k-ые nk предметов – в к-ый ящик. Так как нас не интересует порядок предметов в ящике, то любая перестановка первых n1 предметов не меняет результат раздела. Точно так же его не меняет любая перестановка вторых n2 предметов,..., k-ых nk предметов. По правилу произведения получаем n1! ×n2!×...×nk! перестановок, не меняющих результата раздела. Таким образом, n! перестановок делятся на группы по n1! ×n2!×...×nk! перестановок в каждой группе, причем перестановки из одной группы приводят к одинаковому распределению предметов. Следовательно, число раздела предметов равно 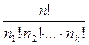 =P(n1,...,nk).
=P(n1,...,nk).
Задача.
При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?
Решение.
Переформулируем задачу: необходимо разложить 28 предметов в 4 ящика по 7 предметов в каждый, причем порядок предметов в ящике не важен. Получаем 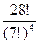 способов распределения костей домино.
способов распределения костей домино.
Можно было рассуждать другим способом. Первый игрок выбирает себе 7 костей из 28, это можно сделать 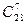 способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать
способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать 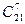 способами. Третьему 7 из 14 –
способами. Третьему 7 из 14 – 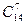 способов. А четвертый заберет оставшиеся. По правилу произведения получаем
способов. А четвертый заберет оставшиеся. По правилу произведения получаем 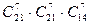 .
.
Даны n различных предметов и k одинаковых ящика. Надо положить в каждый ящик n1 предметов, где n1= 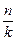 . Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике, и все ящики одинаковы?
. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике, и все ящики одинаковы?
Задача отличается от предыдущей только тем, что ящики не пронумерованы. Так как k ящиков можно переставить k! способами, то полученный в предыдущей задаче результат необходимо разделить на k!. Всего 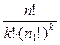 способов распределения.
способов распределения.
Задача.
Сколькими различными способами можно разделить 8 книг на 4 бандероли по 2 книги в каждой?
Решение.
Если бы интересовал порядок бандеролей, то существовало бы  способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого
способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого 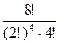 способов разделить 8 книг на 4 бандероли по 2 книги.
способов разделить 8 книг на 4 бандероли по 2 книги.
Сколькими способами можно разложить n одинаковых предметов в k ящиков?
Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных одинаковых предметов и k–1 разделяющих. Каждая такая перестановка определяет один из способов распределения. А именно предметы, расположенные до первого разделителя, положим в первый ящик, предметы, расположенные между первым и вторым разделителем, – во второй ящик и так далее, предметы расположенный после k–1 разделителя, – в k ящик. По формуле перестановок с повторениями число таких перестановок равно P(n, k-1)= 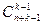 . Значит, всего имеем
. Значит, всего имеем 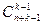 способов разложить n одинаковых предметов в k ящиков.
способов разложить n одинаковых предметов в k ящиков.
Задача.
Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут их разделить, если все яблоки считаются одинаковыми (то есть нас интересует, сколько яблок получит каждый, а не какие именно)?
Решение.
Добавим два разделяющих предмета, тогда получаем Р(40, 2)=780 способа разделить яблоки.
Следствие 1. Если в каждый ящик надо положить не менее r предметов, то получим: P(n-k×r,k-1) способов.
Следствие 2. Если в каждый ящик надо положить хотя бы один предмет, то r=1 и получим P(n-k,k-1)= 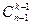 способов распределения.
способов распределения.
Сколько существует способов разложить n различных предметов в k ящиков, если нет никаких ограничений?
Каждый предмет можно положить в любой из k ящиков. Получаем kn способов распределения предметов по ящикам.
Задача.
Сколькими способами можно разделить 8 различных пирожных между 5 детьми?
Решение.
Необходимо разложить 8 предметов по 5 ящикам. Это можно сделать 58=390 625 способами.
Сколькими способами можно поместить n различных предметов в k ящиков, если не должно быть пустых ящиков?
Данные r ящиков остаются пустыми, если в k–r ящиков предметы кладутся без ограничений. r пустых ящиков можно выбрать Cnk способами. В оставшиеся k–r ящиков предметы можно разложить (k–r)n способами. По формуле включений и исключений число распределений, при которых хотя бы один ящик остается пустым, равно 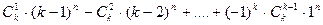 . Тогда количество распределений, при которых ни один ящик не окажется пустым, равно
. Тогда количество распределений, при которых ни один ящик не окажется пустым, равно
kn-(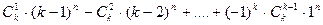 ).
).
Задача.
Сколькими способами можно послать по почте 8 различных фотографий, использовав 5 конвертов?
Разбор.
Переформулируем задачу: необходимо 8 предметов разложить в 5 ящиков. Посылать пустые конверты не рационально, поэтому накладывается запрет на пустые ящики.
Применяя полученную выше формулу, получаем
58-  ×48+
×48+ 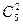 ×38-
×38- 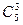 ×28+
×28+ 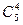 ×18=126 020.
×18=126 020.
Имеется n1 предметов одного сорта, n2 – другого,..., ns – s-го сорта. Сколькими способами их можно разложить по k ящикам, если не должно быть пустых ящиков?
Применяя рассуждения, аналогичные предыдущей задаче, получим следующую формулу
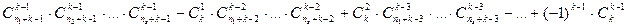 .
.
Задача.
Сколькими способами можно разделить 8 яблок, 10 груш и 7 апельсинов между 4 детьми, если каждый должен получить хотя бы один фрукт?
Решение.
Требуется 8 предметов одного сорта, 10 второго и 7 третьего разложить в 4 ящика так, чтобы ни один ящик не оказался пустым. По предыдущей формуле получаем
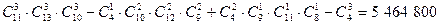 способов такого распределения.
способов такого распределения.
Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем все n предметов должны быть использованы?
Добавим к n предметам k–1 одинаковых разделяющих предмета. Рассмотрим все возможные перестановки из n различных предметов и k–1 одинаковых. Каждая такая перестановка определяет один из способов распределения. Всего таких перестановок 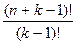 . Значит, n различных предметов можно разложить в k ящиков, с учетом расположения их в ящиках,
. Значит, n различных предметов можно разложить в k ящиков, с учетом расположения их в ящиках, 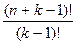 =
= 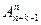 способами.
способами.
К тому же результату можно было прийти и другим путем. Переставим всеми возможными способами данные n предметов (n! способов). Теперь считаем предметы неразличимыми, их можно разложить в k ящиков Р(n, k–1) способами. Получаем n!∙Р(n,k–1)= 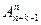 способов распределения этих вещей по к различным ящикам с учетом порядка их расположения в ящиках.
способов распределения этих вещей по к различным ящикам с учетом порядка их расположения в ящиках.
Задача.
Имеются 6 различных сигнальных флагов и 3 мачты, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке вывешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?
Решение.
Имеем 6 предметов, которые необходимо разложить в 3 ящика, причем порядок предметов в ящике важен. Это можно сделать 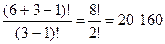 способами.
способами.
Следствие. Если не должно быть пустых ящиков, то выберем k предметов и разложим по одному в каждый ящик. Это можно сделать 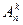 способами. Оставшиеся n–k предметов разложим в k–1 ящик, причем теперь некоторые ящики могут оказаться пустыми. Это распределение можно осуществить
способами. Оставшиеся n–k предметов разложим в k–1 ящик, причем теперь некоторые ящики могут оказаться пустыми. Это распределение можно осуществить 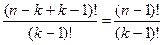 способами. Всего имеем
способами. Всего имеем 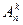
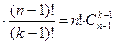 способов распределения.
способов распределения.
Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем не все n предметов могут быть использованы и некоторые ящики могут оказаться пустыми?
Разобьем все возможные комбинации на классы. В s класс войдут комбинации, в которых использованы ровно s предметов. Из предыдущей задачи известно, что s предметов можно разложить по k ящикам 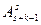 способами. s предметов из данных n можно выбрать
способами. s предметов из данных n можно выбрать 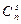 способами. Всего в s класс войдут
способами. Всего в s класс войдут 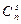 ×
× 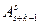 комбинаций. По правилу суммы имеем
комбинаций. По правилу суммы имеем
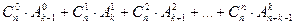 способов распределения n различных предметов по k различным ящикам с учетом порядка их расположения в ящиках, если не все n предметов могут быть использованы.
способов распределения n различных предметов по k различным ящикам с учетом порядка их расположения в ящиках, если не все n предметов могут быть использованы.
Задача.
Имеются 6 различных сигнальных флагов и 3 мачты, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке вывешены флаги. Сколькими способами можно развесить флаги, если не все флаги могут быть использованы и некоторые из мачт могут оказаться пустыми?
Решение.
Имеем 6 различных предметов, которые необходимо разложить в 3 ящика, причем порядок предметов в ящике важен и не все ящики и предметы могут быть использованы. По формуле получаем
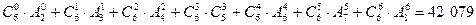
Следствие. Если не должно быть пустых ящиков, то в этом случае имеем
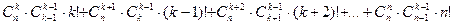 способов распределения.
способов распределения.
Вероятность
Частотой появления события в серии испытаний называется отношение числа наступления этого события в данной последовательности испытаний к общему числу испытаний.
Вероятностью случайного события называется отношение числа равновозможных элементарных событий, благоприятствующих этому событию, к числу всех равновозможных элементарных событий.
Равновозможными элементарными событиями будем считать такие события, любое из которых по отношению к другим событиям не обладает никаким преимуществом появляться чаще другого при многократных испытаниях, проводимых в одинаковых условиях.
Например, при бросании игральной кости возможны шесть различных результатов; из них лишь в одном случае выпадает шестёрка. Поэтому вероятность выпадения шестёрки равна 1/6.
Задача.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 4950; Нарушение авторских прав?; Мы поможем в написании вашей работы!