Достижимость и связность. 36. Являются ли изоморфными графы?

Изоморфизм графов

36. Являются ли изоморфными графы? Ответ обосновать.

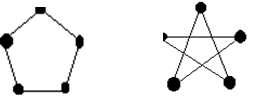37. Докажите, что графы являются изоморфными.

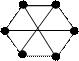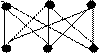38. Докажите, что графы являются изоморфными.

39. 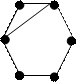Докажите, что графы не изоморфны.

40. Докажите, что графы не изоморфны.

41. Дана матрица смежности графа. Не изображая граф, ответьте на следующие вопросы:

• Какова степень пятой вершины? Назовите смежные с ней вершины.
• Существует ли путь из вершины 2 в вершину 8?

42. Изобразите матрицу достижимости графа.

43.

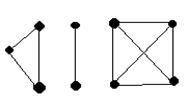Дана матрица смежности графа. Найти все вершины, входящие в одну компоненту связности с вершиной 7.

44. Выделите компоненты связности графа (3 балла)

45. Дана матрица смежности графа. Найдите матрицу достижимостей этого графа, не изображая его.

46. В стране Семерка 15 городов, каждый из которых соединен дорогами не менее чем с 7 другими. Докажите, что из любого города можно добраться до любого другого (возможно, проезжая через другие города).

47. Докажите, что граф с n вершинами, степень каждой из которых не менее (n–1)/2- связен.

48. В некотором государстве лишь один вид транспорта – автомобиль. Из столицы выходит 21 автомобильная дорога, из города Дальний - одна, а из всех остальных городов - по 20. Докажите, что из столицы можно доехать в Дальний (возможно, с пересадками).

49. В стране из каждого города выходит 100 дорог и от любого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь от любого города можно добраться до любого другого.

50. Докажите, что если в графе все вершины имеют четную степень, то в графе нет ребра, удаление которого приводит к увеличению количества компонент связности.

51. В одной стране каждая пара городов соединена только одним транспортным маршрутом: или железнодорожным, или автобусным. Докажите, что существует вид транспорта, которым можно доехать из любого города страны в любой другой (возможно, с пересадками)

52. Докажите, что либо сам граф, либо дополнение к нему является связным.

53. На конференции по новым информационным технологиям студент Иванов познакомился с 52 студентами из разных городов России. По окончании конференции некоторые пары студентов обменялись адресами, причем у каждого из участников конференции оказалось не менее 26 адресов. Через некоторое время Иванову понадобилось узнать адрес студента Петрова, который также участвовал в конференции. Докажите, что Иванов может узнать адрес Петрова.

54. Каждый из семи мальчиков имеет не менее трех братьев. Докажите, что все мальчики – братья.

55. Докажите, что если выполняется соотношение q>(p-1)∙(p-2)/2, где q – количество ребер, а p количество вершин, то граф связен.

56. Докажите, что если граф с q ребрами и p вершинами связен, то (p-1)<=q<=(p-1)∙p/2.

57. 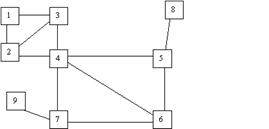На рисунке изображен граф. Найдите:

· ребра графа, являющиеся мостами;

· точки сочленения графа;

· двусвязные компоненты.

58. Докажите, что ребро в графе является мостом тогда и только тогда, когда оно не содержится ни в одном из циклов.

59. На озере 7 островов (1 – 7), которые соединены мостами:

1 с 2 и 4;

2 с 1, 3 и 5;

с 2 и 4;

4 с 1 и 3;

5 с 2, 6 и 7;

6 с 5 и 7;

7 с 5 и 6.

Определить, можно ли с любого острова добраться на любой и существует ли мост, при уничтожении которого это сообщение между островами нарушается.

Дата добавления: 2015-01-03