Правило суммы

Правило произведения

Семенова Ольга Геннадьевна

Элементы дискретной математики

Редактор Иванова Н.А.

Подписано в печать 30.11.05 Формат бумаги 80х64 1/16

Печ. л. 5.5 Заказ 123 Тираж 100 экз.

Редакционно-издательский отдел Ярославского государственного педагогического университета имени К.Д.Ушинского (ЯГПУ)

150000, Ярославль, Республиканская, 108

ЛР №020080 от 19.12.97

Задача.

В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?

Решение.

Чашку можно выбрать 5 способами. Для каждого способа выбора чашки существует 3 способа выбора блюдца. Таким образом, имеем 5∙3=15 способов выбора пары предметов.

Если некоторый объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А, В) можно осуществить m∙n способами. Это утверждение называют правилом произведения.

Для доказательства правила произведения заметим, что каждый из m способов выбора объекта А можно совместить с n способами выбора объекта В. А это приводит к m∙n способам выбора пары (А, В).

Может возникнуть ситуация, когда необходимо составить комбинацию из большего числа элементов.

Задача

В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?

Решение.

Из решения предыдущей задачи известно, что существует 5∙3=15 способов выбора пары предметов чашка – блюдце. Для каждого способа выбора этой пары существует 4 способа выбора ложки. Таким образом, по правилу произведения имеем 5∙3∙4=60 способов выбора комплекта из чашки, блюдца и ложки.

Задача.

Из города А в город Б ведет 6 дорог, а из города Б в город В – 4 дороги, Из города А в город Г – 2 дороги, и из города Г в город В – тоже 2 дороги. Сколькими способами можно проехать от А до В?

Решение.

Из города А в город В можно попасть либо через город Б, либо через город Г. По правилу произведения через город Б можно проехать 6∙4=24 способами, через город Г – 2∙2=4 способами. Тогда из города А в город В можно попасть 24+4=28 способами.

Часто удается разбить все изучаемые комбинации на несколько классов, причем каждая комбинация входит в один и только один класс. В этом случае общее число комбинаций равно сумме чисел комбинаций во всех классах. Это утверждение называют правилом суммы.

Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами.

При использовании правила суммы необходимо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-нибудь способом выбора объекта В.

В рассмотренной выше задаче число выборов после каждого шага зависит от того, какие элементы были выбраны на предыдущих шагах. Рассмотрим пример ещё одной такой задачи.

Задача.

Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая по правилам игры комбинация.

Решение.

Шахматное поле имеет 64 клетки, поэтому белого короля можно поставить 64 способами. Как известно, король бьет клетки, расположенные непосредственно рядом с ним. Таким образом, если король находится в углу, то под боем находятся 3 клетки, если у стены, то – 5, если в центре, то – 8. Очевидно, что ставить черного короля нельзя в ту же клетку, где находится белый король и в клетку, которая находится под боем. Так как существует 4 способа поставить короля в угол, 24 способа – у стены и 36 способов – в центре поля, то ответ на вопрос задачи вычисляется следующим образом: 4∙(64-4)+24∙(64-6)+36∙(64-9)=3612

Рассмотрим теперь вопрос, как вычислить количество способов выбора объекта «либо А, либо В», если известно, что некоторые из способов выбора объекта А совпадают с некоторыми способами выбора объекта В?

Формула включения и исключения.

Задача.

Из-за различия программ в школах Ярославской области студенты первого курса физико-математического факультета разделились на следующие группы: 47 человек знают алгоритмический язык, 35 – язык программирования Паскаль и 23 – оба языка программирования. Сколько человек на курсе знают хотя бы один язык программирования?

Решение.

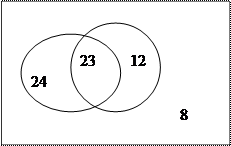Разобьем всех студентов на группы. Первую из них составят те, кто знает только алгоритмический язык, вторую – те, кто знает только Паскаль, третью – те, кто знает оба языка, четвертую – те, кто не знает ни одного.

Количество студентов, знающих хотя бы один язык программирования, можно записать в виде

59=23+24+12=23+(47-23)+(35-23)=47+35-23.

Таким образом, к числу студентов, знающих алгоритмический язык необходимо прибавить число знающих язык Паскаль. При этом некоторые студенты попадают в оба списка и оказываются «прибавленными дважды». Это как раз те, которые знают оба языка программирования. Вычитая их число, получаем число студентов, знающих хотя бы один язык.

Запишем формулу в общем виде.

Обозначим через а1 свойство студента знать алгоритмический язык, через а2 – свойство студента знать Паскаль, через N(а1) – количество студентов, знающих алгоритмический язык, через N(а2) – количество студентов, знающих Паскаль. Тогда

N(а1или а2)= N(а1)+N(а2)-N(а1и а2).

Эту формулу называют формулой включения и исключения.

Задача.

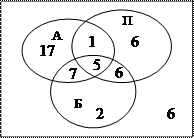Теперь усложним задачу. Пусть 47 студентов знают алгоритмический язык, 35 – язык Паскаль, 23 – Паскаль и алгоритмический язык, 20 – знают Бейсик, 12 – алгоритмический язык и Бейсик, 11 – Паскаль и Бейсик, 5 – все три языка. Вопрос тот же: Сколько человек на курсе знают хотя бы один язык программирования?

Решение.

Решая эту задачу аналогично предыдущей, получим: 47+35+20-23-12-11+5=61.

Используя обозначения, предложенные выше, получаем следующую формулу для трех свойств:

N(а1или а2 или а3)= N(а1)+N(а2)+N(а3)-N(а1и а2) -N(а1и а3) -N(а2и а3) +N(а1и а2 и а3)

Дата добавления: 2015-01-03