Единицы измерения информации

Одну и ту же информацию можно представить и передать по-разному. В старинном телеграфе с помощью азбуки Морзе—в виде точек и тире. В книгах в виде текстов и изображений и т.д.

В современной вычислительной технике информация чаще всего кодируется с помощью последовательностей сигналов всего двух видов:: намагничено или не намагничено, включено или выключено, высокое или низкое напряжение и т.д. Принято обозначать одно состояние цифрой 0, а другое —цифрой 1. Такое кодирование называется двоичным кодированием, а цифры 0 и 1 битами ( от англ. bit—binary digit —двоичная цифра).

При двоичном кодировании текстовой информации каждому символу сопоставляется его код — последовательность из фиксированного количества нулей и единиц. В большинстве современных ЭВМ (электронная вычислительная машина)каждому символу соответствует последовательность из 8 нулей и единиц, называемая байтом (англ. byte), т.е. 1 байт=8 бит. Всего существует 256 (2⁸) разных последовательностей из 8 нулей и единиц — это позволяет закодировать 256 разных символов (большие и малые буквы русского и латинского алфавитов, цифры, знаки препинания и т.д.). Соответствие байтов и символов задается с помощью таблицы, в которой для каждого кода указывается соответствующий символ. Очень часто используется код ASCII (American Standard Code for Information Interchange – американский стандартный код обмена информацией).

Последовательностями нулей и единиц можно закодировать и графическую информацию. Если это только черные и белые точки, то каждую из них можно закодировать 1 битом. Два бита позволяют закодировать 4 оттенка точек: 00-белый цвет, 01- светло-серый, 10- темно-серый, 11-черный.

3 бита позволяют закодировать 8 оттенков и т.д.

Как узнать количество информации в сообщении, в каких единицах измерять информацию? Для двоичных сообщений в качестве такой числовой меры используется количество бит в сообщению. Это количество называют информационным объемом сообщения.

Биты и байты используются также для измерения “емкости” памяти и для измерения скорости передачи двоичных сообщений (бит/сек).

Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа "орел"—"решка", "чет"—"нечет" и т.п.).

В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд.

Бит — количество информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза.

Наряду с битами и байтами для измерения количества информации в двоичных сообщениях используются и более крупные единицы:

Бит, байт, килобайт, мегабайт, гигабайт—много это или мало?

В коде ASCII каждый символ—это 1 байт. На странице учебника помещается порядка 50 строк, в каждой строке примерно 60 знаков(60 байт).
Одна страница учебника имеет информационный объем порядка 3000 байт

Если на условной шкале изобразить бит как 1.25 мм, то байт=8 бит на этой шкале равен 1 см, килобайт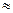

10 м, мегабайт

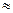10 км, гигабайт

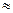10000 км (это расстояние от Москвы до Владивостока) и т.д.

Какое количество информации содержится, к примеру, в тексте романа "Война и мир", во фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро. А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является следующий вывод:

В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.

В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте. Эти подходы используют математические понятия вероятности и логарифма. Если вы еще не знакомы с этими понятиями, то можете пока пропустить этот материал.

Подходы к определению количества информации. Формулы Хартли и Шеннона. Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли: I = log₂N Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log₂100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. Приведем другие примеры равновероятных сообщений: 1. при бросании монеты: "выпала решка", "выпал орел"; 2. на странице книги: "количество букв чётное", "количество букв нечётное". Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины. Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона: I = — (p₁log₂ p₁ + p₂ log₂ p₂ +... + p_N log₂ p_N), где p _i — вероятность того, что именно i -е сообщение выделено в наборе из N сообщений. Легко заметить, что если вероятности p₁,..., p_N равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.

Обработка информации — получение одних информационных объектов из других информационных объектов путем выполнения некоторых алгоритмов [15].

Обработка является одной из основных операций, выполняемых над информацией, и главным средством увеличения объёма и разнообразия информации.

Средства обработки информации — это всевозможные устройства и системы, созданные человечеством, и в первую очередь, компьютер — универсальная машина для обработки информации.