Решение задач 139—154 из учебника

Задача 139. Ученики впервые встречаются с конструкцией повторения, поэтому необходимо проследить, все ли правильно понимают её смысл. Например, стоит обсудить, зачем в конструкции нужно слово КОНЕЦ или зачем конструкция заключена в отдельную оболочку. Если у ребят возникнет затруднение, попросите записать программу Т без оболочек и слова КОНЕЦ и поинтересуйтесь, какие команды будет повторять Робик и сколько раз: Робик повторит все команды, следующие за строкой ПОВТОРИТЬ 4 РАЗА, и результат выполнения программы будет совершенно иным, нежели при выполнении исходной программы Т. Слово КОНЕЦ указывает, что команды, которые нужно повторять, закончились. Заключение конструкции в отдельную оболочку-бусину, с одной стороны, подчёркивает целостность оператора повторения (от слов ПОВТОРИТЬ... РАЗ до слова КОНЕЦ). С другой стороны, такая оболочка оставляет программу, содержащую конструкцию повторения, по-прежнему цепочкой — на этот раз бусинами цепочки являются как отдельные команды, так и целые конструкции. Выделение служебных слов конструкции (ПОВТОРИТЬ, КОНЕЦ) другим шрифтом несёт важную смысловую нагрузку. Цель — отделить эти служебные слова от собственно команд исполнителя. Все эти вопросы необязательно сразу обсуждать со всем классом. Возможно, кто-то из самых любопытных учеников задаст вопросы — вам нужно быть к ним готовым.

Ученикам, которые запутались, предложите обводить на поле повторяющиеся рисунки, получаемые при выполнении конструкции повторения: так будет несложно проверить, во-первых, что они получаются одинаковыми, а во-вторых, что их получилось именно 4.

Решение задачи:

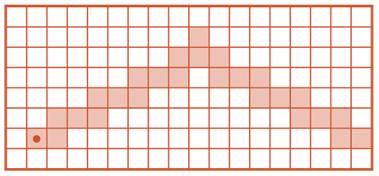
Задача 140. Чтобы избежать ошибок при выполнении программы с конструкцией повторения, можно не только обводить повторяющиеся рисунки на поле. Можно ставить пометки и в программе: например, ставить галочку около слова КОНЕЦ в тот момент, когда очередное выполнение внутренних команд цикла закончено. Как только галочек станет столько, сколько указано после слова ПОВТОРИТЬ, выполнение этой конструкции повторения нужно закончить.

Решение задачи:

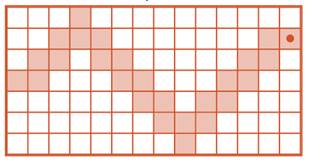
Задача 141. Дети начинают учиться писать программы с новой конструкцией. В этой задаче они опираются на готовую структуру и лишь вписывают команды в окна, но и этого вполне достаточно, чтобы почувствовать себя соавторами программы О. Результаты выполнения программы будут совершенно разными, в зависимости от того, какие именно команды впишет учащийся. Размеры поля позволяют выполнить любую из возможных программ. Однако такая свобода для ребёнка будет сильно осложнять вам этап проверки. Можно попробовать осуществить парную проверку, когда после окончания решения ученики меняются решениями и выполняют программы друг друга на запасном поле со вкладыша тетради проектов, а потом сопоставляют результаты.

Задача 142. Чтобы быстро и аккуратно просматривать слова в столбике и фиксировать наличие в них двух одинаковых букв, нужно придумать какой-то способ. Например, помогут пометки: можно ставить точку около уже просмотренного слова и даже отмечать в нём две одинаковые буквы. Некоторая логическая тонкость может состоять в том, чтобы прекращать просмотр столбца, как только в нём найдётся слово, в котором нет двух одинаковых букв.

Слова, находящиеся в мешках, знакомы детям, но кто-то может не знать или неправильно понимать значения слов «фуфайка», «деверь», «касторка». Хорошо бы найти непонятные слова в словаре и вообще приучить ребят не пропускать в речи или тексте непонятные слова.

Ответ: условию задачи удовлетворяет мешок Q.

Задача 143. В задаче впервые встречается то, что в программировании называется вложенным циклом, — мы несколько раз выполняем программу, а сама эта программа содержит участки, выполняемые по несколько раз. Надеемся, что задача не вызовет у детей трудностей, ведь они уже видели и цепочки внутри цепочки, и мешки внутри мешка, и (в математике) скобки внутри скобок.

Начать решение нужно с выполнения программы Ж. Позиция после выполнения программы Ж показана на рисунке.

Дальнейшее решение состоит из двух этапов. Первый — убедиться с помощью рассуждений, что при выполнении программы Р Робик проходит тот же путь, что и при выполнении программы Ж. Второй — ещё раз убедиться в этом, выполнив программу Р. Возможно, интереснее попросить ребят сначала выполнить программу Р, поскольку некоторым ученикам может быть скучно выполнять программу с заранее известным результатом и они отнесутся к заданию формально. Приготовьтесь к тому, что при всей простоте выполнение программы Р может вызвать вопросы из-за новой конструкции вложенного цикла. Интересно и необходимо выслушать рассуждения ребят, почему результаты выполнения программ получились одинаковыми. После того как задача решена, можно спросить ребят, какую из программ легче читать, понимать и выполнять.

Задача 144. Некоторые дети нарисуют бусины первого уровня, потом к ним присоединят заданные бусины второго уровня, а к ним приделают листья. Таким детям нужно предложить снова вернуться к условию — в дереве должно быть ровно два уровня бусин.

Если ребёнок любит рассуждать, то он, скорее всего, использует следующие соображения. Так как дерево имеет два уровня, то все бусины второго уровня — листья. Однако не все листья — бусины второго уровня, значит, остальные листья — бусины первого уровня. В данном случае корневая жёлтая круглая бусина — лист, а синяя квадратная — не лист.

Задача 145. Заготовка для программы задаёт число конструкций повторения: их должно быть пять. Поскольку узор тоже состоит из пяти прямых участков, по содержанию задача не слишком сложная. Здесь важно только не сбиться и правильно подсчитать число выполнений того или иного повторяющегося участка. Для этого, во-первых, нужно правильно подсчитать число клеток на поле по вертикали и по горизонтали, а во-вторых, сообразить, что на первую клетку каждого отрезка пути Робику не надо шагать — он на ней уже стоит. Для проверки предлагается выполнить написанную программу на запасном поле и сравнить результаты. Главное, чтобы учащиеся не отнеслись к заданию формально, просто подогнав результат под данную в условии позицию.

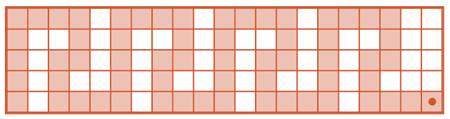
Решение задачи:

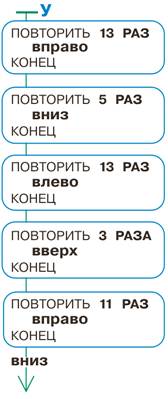
Задача 146. Место для буквы В найдётся быстро. Дальше ребята начнут действовать каждый по-своему. После того как получится ответ — слово ТЕТЕРЕВ, можно спросить, что оно означает, попросите найти это слово в большом толковом словаре.

Задача 147. Эта задача на толкование слов из числа несложных. Все толкования в ней либо совпадают со словарными, либо полностью им противоречат. Поэтому данную задачу можно использовать для текущей проверки темы «Толкования слов» — к настоящему моменту с подобными задачами должны справлять все учащиеся.

Ответ: предпоследнее и последнее утверждения истинные, а остальные ложные.

Задача 148. В задаче требуется преобразовать программу, найдя в ней повторяющиеся участки и переписав их с использованием конструкции повторения. Кто-то может отметить, что при этом программа не стала короче, она занимает столько же, или почти столько, или даже больше места. Спросите, стала ли программа понятнее, легче ли её читать. Постарайтесь добиться понимания того, что программа стала лучше восприниматься человеком и что такую программу проще выполнять и машине.

Дети могут по-разному выделить циклические участки. Здесь не ставится задача достичь полной оптимальности, важны лишь правильность преобразования, эквивалентность исходной программы и полученной. Например, условию удовлетворяет следующая программа:

Вопрос об оптимальности программы, пожалуй, слишком сложный, чтобы мы могли его на этом этапе обсудить со всеми детьми — дать лист определений, достичь общей договорённости. Мы можем сравнивать две программы, дающие один результат, только как цепочки — по их длине. При этом каждая конструкция повторения считается одной бусиной. Но такое сравнение похоже на сравнение программ по оптимальности только в случае, если все конструкции в них одинарные, т. е. внутри конструкции повторения нет других конструкций, как, например, в программе Р задачи 143.

В связи с этим в курсе нет заданий на создание минимальной или оптимальной программы. Вы можете попросить сильных учеников написать другую, более короткую программу. Для работы со всем классом задачу можно использовать как повод дополнительно поиграть или порассуждать с учащимися. Например, можно попросить ребят выписать все различные варианты своих программ на доске, затем выбрать экспертов (которые будут в роли Робиков) и попросить выбрать, на их взгляд, наиболее понятную и простую для исполнения программу. В данном случае наиболее простой, понятной и одновременно наиболее короткой будет программа, данная на следующем рисунке.

Задача 149. Задача на повторение листа определения «Склеивание цепочек», использующая русские слова. Обратите внимание, что разбиение слова здесь происходит не по правилам русской морфологии.

Задача 150. В этой задаче стоит уделить внимание первому утверждению: «Антрацит — это каменный уголь». Как видите, здесь предложено неполное толкование, дети уже встречали такие неполные толкования в задаче 134. В словаре написано: «Антрацит — лучший сорт каменного угля» (это истинное утверждение). Верно ли, что «антрацит — это каменный уголь»? Да, верно. Значит, наше утверждение тоже истинно. С определением истинности остальных утверждений ученики вполне справятся самостоятельно.

Ответ: первое, третье и пятое утверждения истинны, остальные ложны.

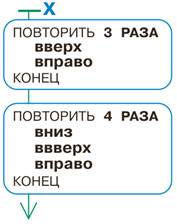
Задача 151. Необходимо выполнить программу с вложенным циклом, но в отличие от задачи 144 результат неизвестен и его нельзя предугадать. Дети должны аккуратно выполнить программу. Трудности возникнут у ребят, которые попытаются одновременно считать количество повторений внешнего и внутреннего циклов. Посоветуйте им обводить на поле рисунок после выполнения всех команд начиная от записи ПОВТОРИТЬ 4 РАЗА и до записи КОНЕЦ. Это поможет не допустить ошибок при переходе от одной такой части к следующей. Кроме того, можно ставить пометку около слова КОНЕЦ всякий раз после выполнения всех команд, находящихся после записи ПОВТОРИТЬ 4 РАЗА и до записи КОНЕЦ. Как только наберётся четыре пометки, нужно остановиться. Для быстрой проверки спросите, где теперь находится Робик.

Решение задачи:

Задача 152 и задача 153 (необязательная). В отличие от предыдущих подобных задач на склеивание/разрезание слов для решения этих задач необходимо использовать информацию из курса русского языка. Если в вашей школе есть возможность проведения интегрированных уроков, эту и подобные задачи (которые встречаются и дальше) можно выбрать для решения на таких уроках.

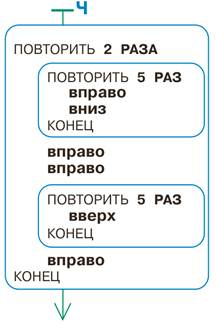
Задача 154. Эта задача напоминает задачу 145. Но здесь заготовка программы вынуждает ребёнка использовать конструкцию вложенного цикла. Это означает, что рисунок, закрашенный Робиком, должен состоять из нескольких одинаковых частей (и в каждой части есть ещё мини-циклы). Сначала надо выделить в узоре такие части и сосчитать их число (2). Одна такая часть — рисунок, который закрашивает Робик, выполняя внутренние команды большого (внешнего) цикла 1 раз. Осталось написать эти команды — теперь задача стала аналогична задаче 145.

Решение задачи:

Уроки «Склеивание мешков цепочек»

Дети уже знакомились в курсе с операцией над цепочками. Теперь им предстоит освоить ещё одно действие, но теперь уже над мешками цепочек. Как видно из листа определений, в результате склеивания двух мешков цепочек получается снова мешок цепочек. В нём лежат все такие цепочки, начало которых — это цепочка из первого мешка, а конец — цепочка из второго мешка. Из этого следует сразу несколько важных свойств (отражённых на листе определений). Операция склеивания мешков не обладает переместительным свойством, т. е. от перемены мест аргументов результат меняется. Во многом (кроме переместительного свойства) эта операция напоминает умножение. Первое сходство — количество цепочек в мешке-результате. Нетрудно догадаться, что для подсчёта достаточно перемножить число цепочек в первом и втором мешках. Второе сходство — наличие элементов, поведение которых сходно с поведением нуля и единицы при умножении. Пустой мешок при склеивании с любым мешком дает пустой мешок ровно так же, как ноль при умножении на любое число дает ноль. Мешок с одной пустой цепочкой в нём при склеивании с любым мешком даёт тот же самый мешок, как единица при умножении на любое число даёт то же число.

Операция склеивания мешков имеет комбинаторный характер: чтобы правильно её выполнить, нужно построить все пары из цепочек первого мешка и цепочек второго мешка. Чтобы не забыть никаких цепочек и не написать лишних, удобно использовать дерево, таблицу или некоторую стратегию, позволяющую не сбиваться. Вот один из таких способов. Берём одну цепочку первого мешка (ставим около неё галочку) и начинаем по очереди приклеивать к ней цепочки второго мешка, перебирая их сверху вниз. Как только очередная цепочка второго мешка использована, ставим около неё галочку. Когда мы добрались до конца второго мешка и около каждой его цепочки стоит по одной галочке, берём вторую цепочку первого мешка и снова склеиваем её с каждой цепочкой второго мешка и т. д. Нетрудно заметить, что процесс склеивания мешков напоминает процесс умножения многочлена на многочлен.

Дата добавления: 2015-01-03