Ex. 17. Translate into English

Monomials and Polynomials

Ex. 16. Translate into Russian.

1. Algebraic expressions are divided into two groups according to the last operation indicated. 2. A monomial is an algebraic expression whose last operation is neither addition not subtraction. 3. So, a monomial is either a separate number represented by a letter or by a figure, for example -x, +9, or a product, for example ab, (x+y), or a quotient, for example 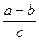, or a power x³, but must never be either a sum or a difference. 4. An algebraic expression which consists of several monomials connected by the plus and minus signs, is known as a polynomial. 5. Such is, for instance, the expression x + yz + c-3 + 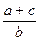6. Terms of a polynomial are separate expressions which form the polynomial by the aid of the + and - signs. 7. Usually the terms of a polynomial are taken with the signs preceding them; for instance, we say: term -a, term +b³ and so on. 8. When there is no sign before the first term it is xy or + xy.

1. Алгебра – это система правил, касающихся действий с числами. 2. В алгебре числа обозначаются буквами, а не цифрами. 3. Поскольку буквы обозначают числа, все законы арифметики годны для действий с буквами. 4. Знаки, которые обозначают действия с цифрами, также употребляются для букв. 5. Операции сложения, вычитания, умножения, деления, возведения в степень и извлечения корней называются алгеб­раическими операциями. 6. В алгебре мы применяем следующие знаки: плюс, минус, знак равенства, знак умножения, знак деления, скобки круглые, квадратные и фигурные, знак «больше, чем», знак «меньше, чем» и другие. 7. Алгебраическому выражению можно придать более простую форму путём приведения подобных членов. 8. Алгебраическая сумма нескольких одночленов называется многочленом. 9. Двучлен – это алгебраическое выражение, состоящее из двух членов, трёхчлен – алгебраическое выражение, состоящее из трёх членов.

Дата добавления: 2014-12-23