Решение. 1) Рассчитаем показатели оборачиваемости оборотных средств: коэффициент оборачиваемости, коэффициент закрепления

1) Рассчитаем показатели оборачиваемости оборотных средств: коэффициент оборачиваемости, коэффициент закрепления, продолжительности одного оборота.

К_об.п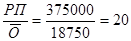р = обор.

К_об.отч. = 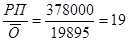обор.

К _зак.пр.= обор.

К _{зак.отч.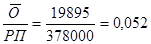} = обор.

П пр.= 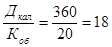дней

П пр.= дней.

2) Определим сумму оборотных средств, высвободившихся вследствие ускорения их оборачиваемости:

= (0,052-0,05)*378000=756 тыс. руб.

Итак, в отчетном году по сравнению с предыдущим годом использование оборотных средств улучшилось.

Задача 1

При выборочном бесповторном собственно-случайном отборе 5% коробок конфет со стандартным весом 20 кг получены следующие данные о недовесе

Недовес 1 коробки, кг	0,4-0,6	0,6-0,8	0,8-1,0	1,0-1,2	1,2-1,4
Число обследованных коробок

Определите:

1) средний недовес одной коробки конфет и его возможные пределы (с вероятностью Р=0,954);

2) долю коробок с недовесом до 1 кг;

2) возможные пределы доли коробок с недовесом до 1 кг (с вероятностью 0,683). Сделайте выводы.

Решение:

Для проведения расчетов заполним вспомогательную расчетную таблицу, предварительно заменив интервалы недовеса одной коробки на их средние значения:

Недовес 1 коробки, кг	fi	xi	хifi	(xi-x)^2*fi
0,4 – 0,6		0,5		1,73056
0,6 – 0,8		0,7	12,6	0,839808
0,8 – 1,0		0,9	32,4	0,009216
1,0 – 1,2		1,1	28,6	0,880256
1,2 – 1,4		1,3		1,47456
Итого		-	91,6	4,9344

1) Средний недовес одной коробки конфет:

(кг)

Пределы для генеральной средней задаются формулой:

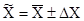
или

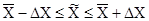
Предельная ошибка выборки для средней:

Дисперсия:

N = 100×100/5 = 2000

При вероятности: P = 0,954 → коэффициент доверия: t = 2

∆Х =

Пределы для средней: = 0,916 ± 0,044 или

0,916 – 0,044 < < 0,916 + 0,044

0,872 < < 0,96

2) Доля коробок с недовесом до 1 кг:

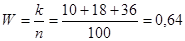(64%)

3) пределы для доли:

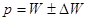
или

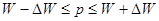
При P = 0,683 → t = 1

Предельная ошибка для доли:

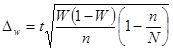
Пределы для доли:

p = 0,64 ± 0,047

или

0,64 – 0,047 £ p £ 0,64 + 0,047

0,593 £ p £ 0,687

или

59,3% £ p £ 68,7%

Выводы: на основании проведённых расчётов можно сказать, что средний недовес одной коробки конфет составил 0,916 кг. Средний недовес одной коробки конфет в генеральной совокупности колеблется в пределах от 0,872 до 0,96 кг. - с вероятностью 95,4%; доля коробок с недовесом до 1 кг – в пределах от 59,3% до 68,7% - с вероятностью 68,3%.

Задача 2

Ежегодные темпы прироста реализации товара «А» составили в % к предыдущему году: 1998 –5,5; 1999– 6,2; 2000- 8,4; 2001 – 10,5; 2002 – 9,2.

Исчислите за приведенные годы базисные темпы роста по отношению к 1997 году и среднегодовой темп прироста за 1998-2002 гг.

Решение:

На основании вышеприведённых данных, для удобства необходимых расчётов, составим расчётную таблицу, в которой разместим имеющиеся данные и рассчитанные показатели.

Для расчета базисных темпов роста по отношению к 1997 году применяем взаимосвязь: произведение последовательных цепных темпов роста (в коэффициентах) равно заключительному базисному темпу: 1,055×1,062×1,084×1,105×1,092=1,465 или 146,5%.

Таблица 1.

Годы	Темпы прироста, %	Темпы роста, %
к предыдущему году (цепная система)	к первому (1997 г.) году (базисная система)	к предыдущему году (цепная система)	к первому (1997 г.) году (базисная система)
	-	-	-	100,0
	5,5	5,5	105,5	105,5
	6,2	12,0	106,2	112,0
	8,4	21,4	108,4	121,4
	10,5	34,2	110,5	134,2
	9,2	46,5	109,2	146,5

Рассчитаем среднегодовой темп роста по формуле:

, где

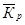- среднегодовой коэффициент роста равен: 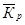= , где

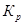(ц.с.) - цепные коэффициенты роста;

тогда среднегодовой темп роста равен:

=107,9%.

Рассчитаем среднегодовой темп прироста по формуле:

=107,9%-100%= 7,9%

Выводы: за исследуемый период времени уровни ряда прирастали в среднем на 7,9%.

Задача 3

Имеются следующие выборочные данные о расходах на платные услуги домохозяйств района:

Домохозяйство	Обследовано домохозяйств	Доля расходов на платные услуги, %
Городское
Сельское

Определите для домохозяйств района:

1. общую дисперсию;

2. среднюю из групповых дисперсий;

3. межгрупповую дисперсию, используя правило сложения дисперсий;

4. эмпирический коэффициент детерминации;

5. эмпирическое корреляционное отношение.

Поясните полученные показатели.

Решение:

Определим для домохозяйств района:

1. Общую дисперсию: =p×(1-p)

Определим среднюю долю расходов на платные услуги:

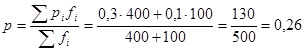, тогда дисперсия равна:

=0,26×(1-0,26)=0,1924

2. Среднюю из групповых дисперсий:

групповая дисперсия для городских домохозяйств:

=p₁×(1-p₁)=0,3×(1-0,3)=0,21

групповая дисперсия для сельских домохозяйств:

=p₂×(1-p₂)=0,1×(1-0,1)=0,09

Тогда средняя из групповых дисперсий:

Межгрупповую дисперсию определим, используя правило сложения дисперсий:

Т. к. , Þ

4. Эмпирический коэффициент детерминации:

5.Эмпирическое корреляционное отношение:

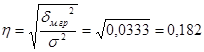
Выводы: по полученным результатам можно сказать, что связь между признаками слабая.

Задача 4

По отделению банка имеются следующие данные о вкладах населения:

Виды вкладов	Базисный период	Отчетный период
Количество счетов	Остаток вкладов, тыс. руб.	Количество счетов	Остаток вкладов, тыс. руб.
Депозитный
Срочный
Выигрышный

Определите

1) Средний размер вклада в базисном и отчетном периодах.

2) Индексы среднего размера вклада:

- переменного состава;

- постоянного состава;

- структурных сдвигов.

Покажите взаимосвязь рассчитанных индексов.

Решение:

Проведем решение задачи в табличной форме:

Вид вкладов	q0	p0q0	q1	p1q1	p0	p1	p0q1
Депозитный					1,02	1,067
Срочный					2,16	1,381
Выигрышный					0,5	0,7
Итого

Определим:

1) средний размер вклада:

в отчетном периоде: тыс. руб.;

в базисном периоде: тыс. руб.

2) Индексы среднего размера вклада:

Индекс переменного состава:

или 93,85%

Индекс постоянного состава равен

или 86,48%

Индекс структурных сдвигов

или 108,54%

Взаимосвязь рассчитанных индексов:

I _пер.с = I _{пост. с} × I_стр.= 0,8648×1,0854 = 0,9386 или 93,86%.

Выводы: в отчетном периоде по сравнению с базисным произошло уменьшение среднего размера вклада на 6,15% (93,85%–100%) всего, в том числе за счет уменьшения размеров вкладов по каждому виду в отдельности на 13,52% (86,48%-100%), но благоприятные изменения в структуре вкладов привели к увеличению среднего размера вкладов на 8,54% (108,54%–100%).

Задача 5

Валовой выпуск товаров и услуг в рыночных ценах в производственной сфере Российской Федерации за отчетный период составил 5130,2 млрд руб., в непроизводственной сфере –1520,9 млрд руб. Условно исчисленная продукция финансового посредничества в экономике составила 126,8 млрд. руб.

Определите валовую добавленную стоимость по сферам деятельности и в целом по экономике, если промежуточное потребление в производственной сфере составило 2790,5 млрд руб., в непроизводственной – 680,3 млрд руб.

Решение:

Валовая добавленная стоимость: ВДС = ВВ-ПП.

Валовая добавленная стоимость в производственной сфере:

ВДС = 5130,2 - 2790,5 = 2339,7 (млрд. руб.)

Валовая добавленная стоимость в непроизводственной сфере:

ВДС = 1520,9 – 680,3 = 840,6 (млрд. руб.)

Валовая добавленная стоимость в целом по экономике:

ВДС = 2339,7+840,6+126,8 = 3307,1 (млрд. руб.)

Задача 6

Имеются следующие данные по области на начало текущего года (тыс. чел.):

Население рабочего возраста
Нетрудоспособное население рабочего возраста	58,5
Фактически работающие пенсионеры и подростки	31,8
Из общей численности трудоспособного населения занято работой и учебой в других областях	12,8
Занято частным предпринимательством	181,8
Занято на производственных предприятиях	564,1
Учащиеся с отрывом от производства рабочего возраста	35,9
Занято в домашнем хозяйстве и уходом за детьми	68,4
Из общей численности занятых и учащихся проживает в других областях	9,3

Определите:

1. численность трудовых ресурсов двумя методами;

2. коэффициенты занятости трудовых ресурсов (с учетом и без учета учащихся).

Решение:

1. Определим численность трудовых ресурсов двумя методами:

Численность трудовых ресурсов определяется следующим образом:

ТР = Т _{трудоспособного возраста} + Т _{неработающих инвалидов 1 и 2 гр. (рабочего возраста)} + Т _{пенсионеров трудоспособного возраста, получающих пенсии по возрасту на льготных условиях} + Т _{фактически работающих подростков и лиц пенсионного возраста}

Численность трудовых ресурсов 1-ым методом определим следующим образом:

ТР = 880-58,5+31,8-12,8 = 840,5 (тыс. чел.) или

Численность трудовых ресурсов 2-ым методом определим следующим образом:

ТР = 181,8+564,1+35,9+68,4-9,3 = 840,9 (тыс. чел.)

2. Коэффициент занятости трудовых ресурсов:

К_з.т.р. = S_з.н.*100/ТР, где S_з.н.- численность занятого населения

- с учетом учащихся:

К_з.т.р. = (181,8+564,1+35,9-9,3)*100/840,9 = 91,9%

- без учета учащихся:

К_з.т.р. = (181,8+564,1-9,3)*100/840,9 = 87,6%

Выводы: часть населения данной области, которая фактически занята в экономике или же незанята, но способна к труду по возрасту и состоянию здоровья, за данный период времени составила 841 тыс. чел. Занятость трудовых ресурсов с учетом учащихся составила - 91,9%, без учета учащихся – 97,6%.

Задача 7

Имеются следующие данные о движении основных производственных фондов (ОПФ) по предприятию в отчетном году (тыс. руб.):

Полная первоначальная стоимость на начало года
Износ ОПФ на начало года
Введено в действие новых ОПФ
Выбыло ОПФ по полной стоимости
Остаточная стоимость выбывших ОПФ
Норма амортизации	9%
Объем продукции (работ, услуг)
Удельный вес активной части ОПФ	55%

Определите:

1) коэффициенты годности ОПФ на начало года;

2) коэффициенты ввода и выбытия ОПФ;

3) фондоотдачу всех ОПФ и активной части;

4) фондоемкость продукции.

Постройте баланс основных производственных фондов по полной и остаточной первоначальной стоимости.

Решение:

1) Остаточная стоимость ОПФ на начало года: ОС_н.г.=3875-2075=1800 тыс. руб.

Коэффициент годности ОПФ на начало года: 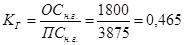или 46,5%

2) Определим наличие ОПФ по полной стоимости на конец года:

ПС_к=ПС_н+П-В=3875+1090-670=4295 тыс. руб.

Коэффициент поступления: 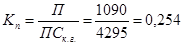или 25,4%

Коэффициент выбытия: 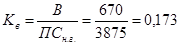или 17,3%

3) фондоотдача вычисляется как отношение объема продукции к среднегодовой стоимости основных фондов. Определим среднегодовую стоимость основных фондов:

тыс. руб., тогда фондоотдача будет равна

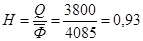руб.

Фондоотдача активной части ОПФ:

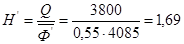руб.

4) фондоемкость продукции

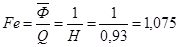руб.

Построим баланс ОПФ по полной первоначальной стоимости

Наличие на начало года	Поступило в отчетном году	Выбыло в отчетном году	Наличие на конец года
Всего	В том числе новых основных фондов	Всего	В том числе ликвидировано

Построим баланс ОПФ по остаточной первоначальной стоимости

Наличие на начало года	Поступило в отчетном году	Выбыло в отчетном году	Износ за год	Наличие на конец года
Всего	В том числе новых основных фондов	Всего	В том числе ликвидировано
					3875×0,09=348,75	2241,25

Задача 1

Уточнение величины валового внутреннего продукта региона провели с использованием распределения малых предприятий по объему выпуска продукции (товаров, работ, услуг), полученного на основе 10 % выборочного наблюдения:

Группы предприятий по объему выпуска продукции (работ, услуг), тыс. руб.	Количество предприятий
До 100,0
100,0-200,0
200,0-300,0
300,0-400,0
400,0-500,0
500,0 и более
Итого:

Определите по предприятиям, включенным в выборку:

а) средний размер произведенной продукции (товаров, работ, услуг) на одно предприятие;

б) долю предприятий с объемом производства продукции более 400 тыс. руб.;

в) средние ошибки показателей объема произведенной продукции и доли предприятий с объемом производства продукции свыше 400 тыс. руб. (с вероятностью 0,954).

Сделайте выводы.

Дата добавления: 2014-12-23