Средние индексы

Средние индексы применяют в том случае, если нет достаточной информации для расчета агрегатного индекса. Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. При вычислении средних индексов применяют 2 формы средних:

1) средняя арифметическая

2) средняя гармоническая

,

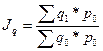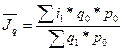- индекс продаж

средний индекс физического объема товарооборота.

Средние арифметические индексы определяются для качественных показателей. Для количественных показателей осуществляется расчет средних гармонических индексов.

НАПРИМЕР: индексные цены

- индекс цены, - индекс себестоимости

По данным предыдущей задачи рассчитать средний индекс цены и средний индекс физический объем производства.

Экономические показатели изменяются во времени и при их изучении необходимо осуществить анализ нескольких индексов. С этой целью строится система индексов. В зависимости от базы сравнения различают систему базисных индексов и систему цепных индексов. Система базисных индексов - это ряд последовательных временных индексов одного и того же явления с постоянной базой сравнения. Система цепных индексов - это ряд индекс одного и того же явления вычисленных с меняющейся базой сравнения.

Система базисных индексов по ; ;

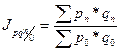
Система базисных методов: ; ;

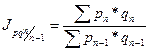
Формирование системы индексов цен физического объема производства, себестоимости и т.д. несколько отличается, т.к. при их построении можно использовать постоянные и переменные веса. Система индексов с постоянными весами - это система общих индексов одного и того же явления, вычисленных с весами, неменяющимися при переходе от одного индекса к другому. Постоянные веса позволяют исключить влияние изменения структуры на величину индекса:

● базисный с постоянными весами: ; ;

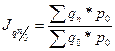
● цепной с весами. В системе индексов с переменными весами. Веса последовательно меняются от одного индекса к другому.

● базисный с переменными весами ;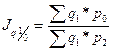

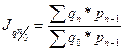
● цепной с переменными весами: ;

Составить системы базисных и цепных индексов цен с постоянными и переменными весами и рассчитать изменение цены по следующим данным.

товар		цена за ед.р.			объем выборки
	январь	февраль	март	апрель	январь	февраль	март	апрель
крупный лесоматериал
тех.цена
дрова

Изменение экономических показателей обусловлено влиянием на них ряда факторов, к которым относят изменение отдельных групп в натуральных единицах измерения и измерение структуры социально экономического явления. При построении индексов возможно определить степень влияния этих двух групп факторов путем построения индекса переменного состава, индекса постоянного состава и индекса структурных сдвигов. Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, которые относятся к разным периодам времени:

- индекс переменного состава

Индекс фиксированного состава - это индекс, рассчитанный с весами, зафиксированными на уровне первого периода, который характеризует влияние группы единиц на явления.

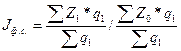- характеризует влияние изменения структуры на динамику среднего уровня явления. Структурный сдвиг будет иметь следующий вид:

Индекс переменного состава на индекс структурного сдвига

ПРИМЕР:

Определить уровень влияния факторов на среднюю цену единицы продукции по предприятию по следующим данным

вид продукции	план		факт
	цена за ед.продукции	объем пр-ва	цена за ед.продукции	объем пр-ва
шерсть
пряжа
скат

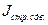, - индекс структурных сдвигов.

1,05- то есть объем производства возрос на 5%

Если из числителя вычесть знаменатель то получим сколько в рублях произошел объем производства это составляет 7600р = 5%

Влияние неучтенных факторов снизилось на 2%, цены на единицу продукции возросли на 7%, что составило 10600.

Динамику изменения показателей по территориям изучают путем построения территориальных индексов. В основу территориальных индексов положены относительные величины, сравнения. При построении территориальных индексов.

,

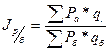Рассчитать индекс физического объема производства и производства пиломатериалов и определить динамику зменения данного показателя по территориям взяв за базу данные территории А

продукт		А	Б		С
	объем пр-ва	цена, р.	объем пр-ва	цена, р.	объем пр-ва	цена, р.
I
II
III

Показателем динамики с применением индексного метода применяется - Фишера и расчет показателей по индексу Фишера позволяет исключить вместе неучтенных факторов: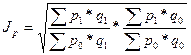

По методике Фишера

Дата добавления: 2014-12-23