Постановка задачи. Тема: «Приближенное вычисление производной от таблично заданной функции на основе интерполяционных многочленов Лагранжа и Ньютона»

Лабораторная работа № 11

Тема: «Приближенное вычисление производной от таблично заданной функции на основе интерполяционных многочленов Лагранжа и Ньютона»

Пусть исследуемая функция либо задана таблично на интервале с постоянным шагом , либо имеет достаточно сложный функциональный вид, затрудняющий определение производной .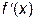

Необходимо построить алгоритм вычисления значения производной в заданной точке , воспользовавшись интерполяционным многочленом:

а) – Лагранжа:

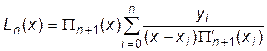, где ; (11.1)

б) – Ньютона (первая и вторая формулы соответственно):

, (11.2)

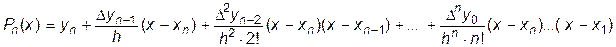. (11.3)

Предполагается, что исходная таблица функции содержит достаточно большое количество отрезков интерполирования, например . Очевидно, что для решения нашей задачи строить интерполяционные многочлены степени 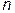нерационально и, кроме того, погрешность самих арифметических операций может существенно возрастать при больших степенях многочленов.

В качестве условия задачи примем следующие границы для степени интерполяционных многочленов (11.1)–(11.3), аппроксимирующих нашу табличную функцию .

Напомним, что для построения интерполяционного многочлена степени нам необходимо использовать отрезков интерполирования (или, что то же, узел интерполирования).

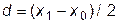Программа, разработанная Вами, должна вычислять таблицу значений производной в узлах исходной таблицы данных, а также в средних ее точках, т.е. для , где и .

Таблиц производных должно быть две – для метода интерполирования по Лагранжу и для метода интерполирования по Ньютону соответственно. В каждой таблице должны приводиться точные значения производной, а также абсолютная и относительная погрешности их вычисления.

Исходные данные (аппроксимируемые функции) необходимо брать из таблицы «Вариантов заданий» к Лабораторной работе № 8. Значения параметров 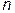и задаются пользователем при непосредственном выполнении программы.

Дата добавления: 2014-12-23