Предварительные рекомендации

Для успешного выполнения данной лабораторной работы Вам следует ознакомиться со следующими рекомендациями.

Рассмотрим особенности реализации алгоритма интерполирования по Лагранжу.

Пусть установлено, что исследуемое значение аргумента 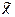принадлежит -му отрезку интерполирования, т.е. .

Введем обозначение 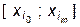для частичного интервала интерполирования, содержащего в себе отрезок 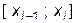, а также ровно отрезков интерполирования ( узел) из исходной таблицы данных:

Наша первоочередная задача – вычислить индексы 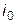и 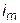узлов-границ частичного интервала 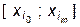при условии, что отрезок 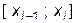должен располагаться «посередине» этого интервала.

Такой подход обеспечит наилучшее для многочлена Лагранжа «качество» аппроксимации табличной функции и ее производной 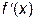для значения аргумента .

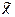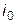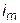Таким образом, алгоритм вычисления значений индексов и представляет собой самостоятельную проблему. По этой причине мы будем его разрабатывать и отлаживать в рамках отдельного, вспомогательного консольного приложения (например, на Fortran).

Указанный алгоритм должен учитывать следующие моменты:

· порядок интерполяционного многочлена может быть как четным, так и нечетным числом;

· значение 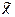аргумента может быть близко к границам ( 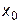или ) исходной таблицы данных, так что указанный выше принцип размещения отрезка 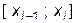«посередине» интервала 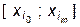не может быть реализован.

Будем определять индексы 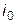и 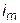с использованием известных арифметических функци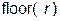й и , выполняющих преобразование действительного числа к целому:

(11.4)

где для четных значений будет (11.5)

а для нечетных значений будет (11.6)

Например, при имеем см. рисунок выше по тексту, (11.7)

а при 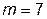имеем 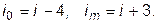(11.8)

Такие результаты обусловлены правилами функци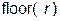й и . Их суть легко усвоить из примера:

(11.9)

Следовательно, первая функция – 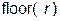– у положительного действительного числа 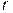просто «отбрасывает» дробную часть, а вторая функция – – увеличивает 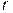до ближайшего целого.

Если при реализации алгоритма (11.4) индекс 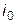оказывается отрицательным, то это означает, что значение аргумента 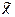размещается «близко» к узлу 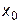и интервал 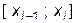нельзя расположить «посередине» интервала .

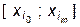В таком случае мы в качестве индекса 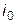будем брать , т.е. , а индексу 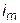дадим значение , т.е. 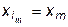. (11.10)

Если же при реализации алгоритма (11.4) индекс 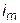окажется больше, чем 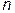, то это означает, что значение аргумента 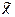размещается «близко» к узлу и интервал 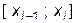также нельзя расположить «посередине» интервала .

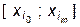В этой ситуации мы поступим аналогично предыдущему случаю: индексу 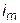дадим значение 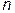, т.е. , а индексу 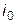– значение 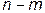, т.е. 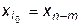. (11.11)

Во всех трех перечисленных случаях для частичного интервала интерполирования будет выделено из основной таблицы ровно интервалов ( узел интерполирования).

Все выше сказанное реализуем в отдельном проекте AddAlgorithm_11 консольного приложения на языке программирования Fortran.

Для простоты анализа результатов массив узлов исходной таблицы разместим в точках с целыми значениями координат, например, равными их индексу, а в качестве «исследуемых» точек 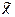будем выбирать середины полученных отрезков интерполирования.

При таких условиях код основной программной единицы будет следующим:

Ниже приводятся результаты для одного из тестовых расчетов:

Вернемся теперь к формуле (11.1). С использованием новой безразмерной переменной ее можно представить в ви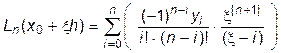де:

, где 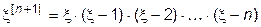. (11.12)

Каждое е слагаемое, стоящее под знаком суммы в (11.12) представляет собой произведение коэффициента на многочлен степени 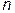, записанный в виде произведения 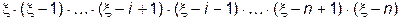, в котором отсутствует скобка .

Производная от многочлена Лагранжа будет иметь вид:

. (11.13)

Таким образом, каждое е слагаемое, стоящее под знаком суммы в (11.13) будет представлять собой произведение коэффициента 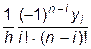на производную от произведения .

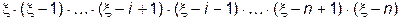Отметим, что в этом произведении всего 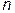сомножителей, поскольку отсутствует скобка .

Производная произведения, в свою очередь, может быть представлена в виде следующей суммы:

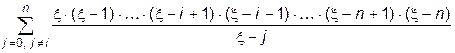. (11.14)

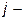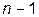Каждое е слагаемое такой суммы является произведением из сомножителей, в котором отсутствуют скобки и .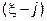

Подведем общий итог рассуждениям. Формула (11.13) представляет собой сумму из 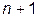слагаемого (по от 0 до 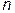), каждое из которых представляет собой сумму (11.14) из 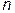слагаемых (по от 0 до 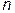, без слагаемого с 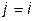), каждое из которых, в свою очередь, есть произведение из 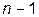сомножителей (по от 0 до 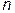, без сомножителей и ).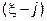

Если при построении многочлена (11.13) мы будем использовать только отрезков интерполирования, непосредственно примыкающих к значению 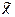, то нам придется воспользоваться уже отлаженным алгоритмом определения границ 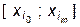частичного интервала интерполирования.

В этом случае параметр 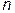в формулах (11.13) и (11.14) будет принимать значение , а безразмерная переменная 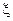будет вычисляться как 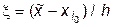, а сама формула (11.13) примет вид

. (11.15)

Остается только реализовать формулу (11.15) в виде соответствующей программной единицы.

Обратимся теперь к формулам (11.2) и (11.3) интерполирования по Ньютону. Выполним в этих формулах замену переменной следующего вида:

· для первой интерполяционной формулы – 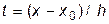, когда ;

· для второй интерполяционной формулы – 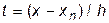, когда .

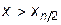Тогда будем иметь (с учетом того, что степень интерполяционного многочлена будет ):

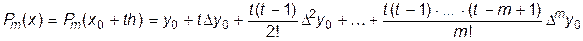, (11.16)

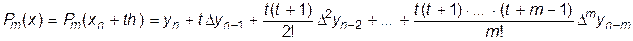. (11.17)

Дифференцирование обеих формул дает следующие выражения:

, (11.18)

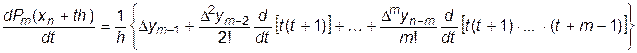. (11.19)

Выше мы уже обсуждали вид производной от произведения нескольких сомножителей. В данном случае каждое из слагаемых (кроме первых) в суммах (11.18) и (11.19) содержит производную от произведения сомножителей, количество которых равно – «номеру» слагаемого в этой сумме. При этом, в отличие от случая Лагранжа, в этом произведении нет «отсутствующих» скобок.

Поэтому алгоритм вычисления слагаемых в суммах (11.18) и (11.19) будет проще:

для го слагаемого в (11.18) ; (11.20)

для го слагаемого в (11.19) 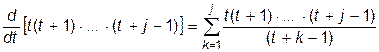. (11.21)

Следующее соображение касается построения таблицы конечных разностей. Поскольку степень интерполяционного многочлена задана, то нет смысла вычислять разности порядков, старше чем .

Теперь Вы можете приступать к непосредственному программированию по данной работе.

Пример выполнения лабораторного задания на Fortran

Воспользуемся уже разработанными компонентами из лабораторных работ № 8 и № 9, а в качестве исследуемой функции возьмем зависимость

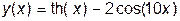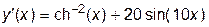, . (11.22)

Стартуем среду разработки MS Visual Studio. Создадим новый проект LabTask_11f и сгенерируем в нем файл основной программной единицы – main_11.f90.

Включим в проект файл y(x)_dy(x).f90 со следующими программными единицами, представляющими собой функции (11.22):

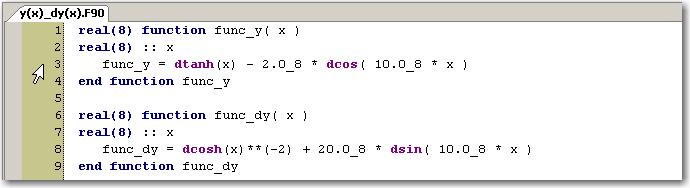
Реализуем алгоритм (11.15) интерполирования по Лагранжу для производной от таблично заданной функции следующим образом:

Здесь переменная xx есть исследуемое значение аргумента .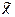

Обозначения всех остальных переменных выполнены максимально близко к обозначениям, принятым в выше приведенных формулах.

Алгоритмы (11.18)–(11.21) интерполирования по Ньютону объединим в рамках одной программной единицы:

Объединим интерфейсы к разработанным программным единицам в рамках одного модуля:

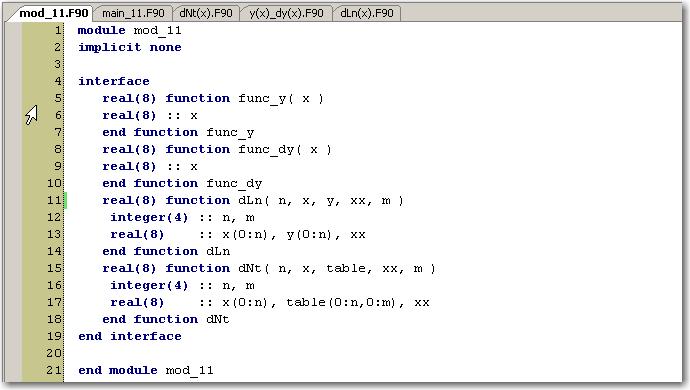
Раздел описаний основной программной единицы может быть следующим:

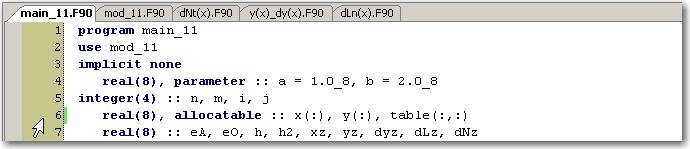
Основные действия программы указаны в комментариях, поэтому мы предоставляем Вам возможность самостоятельно разобраться в сути производимых преобразований над числовыми данными:

Выполнение данной программной единицы требует ввода данных, например:

Таблица результатов (файл Table_dy.txt) интерполирования по Лагранжу для производной функции (11.22) будет иметь следующий вид:

n = 21 m = 7

x y(x) y'(x) Ln'(x) abs_err otn_err

1.0000 2.439737 -10.460448 -10.466503 0.006056 0.058 %

1.0238 2.145598 -14.126488 -14.125279 0.001209 0.009 %

1.0476 1.773570 -16.972276 -16.971319 0.000957 0.006 %

1.0714 1.345186 -18.838069 -18.838239 0.000170 0.001 %

1.0952 0.885142 -19.619399 -19.619747 0.000348 0.002 %

1.1190 0.419897 -19.272966 -19.272930 0.000036 0.000 %

1.1429 -0.023813 -17.819080 -17.818854 0.000226 0.001 %

1.1667 -0.420483 -15.340516 -15.340512 0.000005 0.000 %

1.1905 -0.747283 -11.977845 -11.978087 0.000242 0.002 %

1.2143 -0.985341 -7.921499 -7.921496 0.000002 0.000 %

1.2381 -1.120807 -3.401028 -3.401374 0.000347 0.010 %

1.2619 -1.145637 1.327850 1.327850 0.000000 0.000 %

1.2857 -1.058046 5.997679 5.997304 0.000375 0.006 %

1.3095 -0.862603 10.344354 10.344351 0.000003 0.000 %

1.3333 -0.569982 14.122023 14.121704 0.000319 0.002 %

1.3571 -0.196350 17.116960 17.116955 0.000005 0.000 %

1.3810 0.237539 19.159618 19.159425 0.000193 0.001 %

1.4048 0.707520 20.134202 20.134196 0.000006 0.000 %

1.4286 1.187377 19.985196 19.985172 0.000024 0.000 %

1.4524 1.650325 18.720498 18.720493 0.000006 0.000 %

1.4762 2.070521 16.410976 16.411127 0.000151 0.001 %

1.5000 2.424524 13.186463 13.186460 0.000004 0.000 %

1.5238 2.692615 9.228438 9.228730 0.000292 0.003 %

1.5476 2.859913 4.759781 4.759780 0.000001 0.000 %

1.5714 2.917213 0.032199 0.032568 0.000368 1.130 %

1.5952 2.861505 -4.687973 -4.687972 0.000001 0.000 %

1.6190 2.696149 -9.134808 -9.134445 0.000362 0.004 %

1.6429 2.430680 -13.057780 -13.057776 0.000004 0.000 %

1.6667 2.080273 -16.235910 -16.235634 0.000276 0.002 %

1.6905 1.664887 -18.490230 -18.490224 0.000006 0.000 %

1.7143 1.208140 -19.693879 -19.693751 0.000128 0.001 %

1.7381 0.735975 -19.779267 -19.779261 0.000006 0.000 %

1.7619 0.275198 -18.741884 -18.741932 0.000048 0.000 %

1.7857 -0.148035 -16.640556 -16.640551 0.000005 0.000 %

1.8095 -0.509694 -13.594127 -13.594341 0.000214 0.002 %

1.8333 -0.789229 -9.774757 -9.774754 0.000003 0.000 %

1.8571 -0.970728 -5.398202 -5.398533 0.000332 0.006 %

1.8810 -1.043821 -0.711645 -0.711714 0.000069 0.010 %

1.9048 -1.004256 4.020248 4.020814 0.000567 0.014 %

1.9286 -0.854145 8.530264 8.530586 0.000322 0.004 %

1.9524 -0.601842 12.563720 12.561988 0.001732 0.014 %

1.9762 -0.261473 15.892830 15.890370 0.002460 0.015 %

2.0000 0.147863 18.329556 18.341838 0.012282 0.067 %

Другая таблица, для интерполирования по Ньютону, будет содержать следующие данные:

x y(x) y'(x) Nt'(x) abs_err otn_err

1.0000 2.439737 -10.460448 -10.466503 0.006056 0.058 %

1.0238 2.145598 -14.126488 -14.125279 0.001209 0.009 %

1.0476 1.773570 -16.972276 -16.971319 0.000957 0.006 %

1.0714 1.345186 -18.838069 -18.835940 0.002129 0.011 %

1.0952 0.885142 -19.619399 -19.617813 0.001585 0.008 %

1.1190 0.419897 -19.272966 -19.270390 0.002576 0.013 %

1.1429 -0.023813 -17.819080 -17.817218 0.001861 0.010 %

1.1667 -0.420483 -15.340516 -15.338067 0.002449 0.016 %

1.1905 -0.747283 -11.977845 -11.976122 0.001723 0.014 %

1.2143 -0.985341 -7.921499 -7.919721 0.001777 0.022 %

1.2381 -1.120807 -3.401028 -3.399826 0.001201 0.035 %

1.2619 -1.145637 1.327850 1.328560 0.000710 0.053 %

1.2857 -1.058046 5.997679 5.998091 0.000412 0.007 %

1.3095 -0.862603 10.344354 10.343839 0.000515 0.005 %

1.3333 -0.569982 14.122023 14.121555 0.000468 0.003 %

1.3571 -0.196350 17.116960 17.115335 0.001625 0.009 %

1.3810 0.237539 19.159618 19.158373 0.001245 0.006 %

1.4048 0.707520 20.134202 20.131828 0.002374 0.012 %

1.4286 1.187377 19.985196 19.983451 0.001744 0.009 %

1.4524 1.650325 18.720498 18.717904 0.002595 0.014 %

1.4762 2.070521 16.410976 16.409120 0.001856 0.011 %

1.5000 2.424524 13.186463 13.184225 0.002238 0.017 %

1.5238 2.692615 9.228438 9.226884 0.001554 0.017 %

1.5476 2.859913 4.759781 4.760035 0.000254 0.005 %

1.5714 2.917213 0.032199 0.030950 0.001249 4.036 %

1.5952 2.861505 -4.687973 -4.686562 0.001411 0.030 %

1.6190 2.696149 -9.134808 -9.141842 0.007034 0.077 %

1.6429 2.430680 -13.057780 -13.055525 0.002255 0.017 %

1.6667 2.080273 -16.235910 -16.247165 0.011254 0.069 %

1.6905 1.664887 -18.490230 -18.487633 0.002596 0.014 %

1.7143 1.208140 -19.693879 -19.706850 0.012970 0.066 %

1.7381 0.735975 -19.779267 -19.776907 0.002361 0.012 %

1.7619 0.275198 -18.741884 -18.753684 0.011800 0.063 %

1.7857 -0.148035 -16.640556 -16.638956 0.001599 0.010 %

1.8095 -0.509694 -13.594127 -13.602132 0.008005 0.059 %

1.8333 -0.789229 -9.774757 -9.774275 0.000482 0.005 %

1.8571 -0.970728 -5.398202 -5.400630 0.002428 0.045 %

1.8810 -1.043821 -0.711645 -0.712387 0.000742 0.104 %

1.9048 -1.004256 4.020248 4.023936 0.003689 0.092 %

1.9286 -0.854145 8.530264 8.528463 0.001801 0.021 %

1.9524 -0.601842 12.563720 12.572705 0.008985 0.071 %

1.9762 -0.261473 15.892830 15.890370 0.002460 0.015 %

2.0000 0.147863 18.329556 18.341838 0.012282 0.067 %

Анализ двух представленных таблиц свидетельствует в пользу алгоритма по Лагранжу. Причина этого – принцип размещения значения 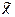«посередине» частичного интервала интерполирования 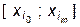, реализованный нами в функции dLn().

Можно отметить, что качество интерполирования по Ньютону может быть всегда улучшено за счет увеличения порядка для старшей конечной разности, участвующей в вычислениях.

Пример выполнения лабораторного задания на языке C#

В имеющемся рабочем пространстве NMM_PetrovIS сгенерируем (добавим) новый проект LabTask_11с консольного приложения на языке программирования C#.

Включим в проект класс – Class_11, в котором разместим программные компоненты – аналоги разработанных выше алгоритмов. Никакие принципиально новые приемы программирования мы здесь использовать не будем, поэтому коды программных компонентов приводим без комментариев:

Кроме того, коды функций func_y() и func_dy() в соответствии с формулами (11.22) Вам уже под силу сформировать самостоятельно.

Напомним здесь, что для сохранения результатов вычислений в виде файла на жестком диске, нам необходимо подключить в основной программной единице пространство имен System.IO.

Аналог основной программной единицы main_11 (на Fortran) на языке C# может иметь, например, следующий вид:

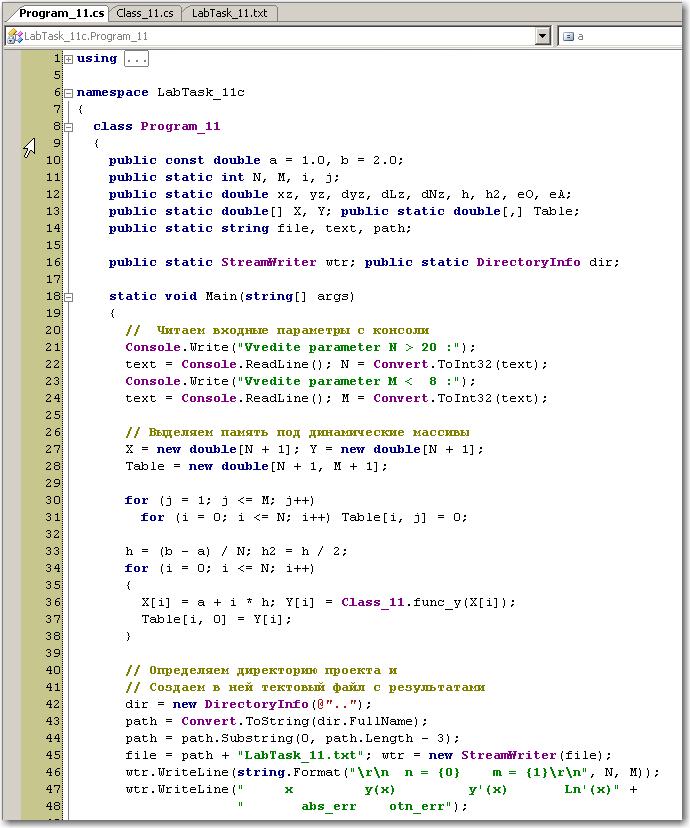
Сравнение кодов на C# и Fortran, реализующих операции форматного вывода в текстовый файл, безусловно, говорит в пользу Fortran. В частности, операторы format позволяют более гибко организовывать форматный ввод/вывод и не «загромождают» основной код программы, поскольку могут быть записаны в любом месте программной единицы (неисполняемые операторы).

Компиляция проекта LabTask_11с и тестовый расчет дают результаты (файл LabTask_11с.txt), идентичные тем, что были получены в проекте LabTask_11f и приведены выше в виде таблиц (файл Table_dy.txt).

Последнее свидетельствует в пользу того, что цель данной лабораторной работы достигнута.

Отладка данной лабораторной работы (на обоих языках программирования) должна производиться на функциях (11.22), а затем на функциях из Вашего варианта.

Только после того, как Вами будут получены результаты, совпадающие с приведенными выше, Вы можете приступать к вычислениям для своих данных.

Контроль выполнения варианта лабораторного задания № 11

Для контроля правильности Вашего выполнения лабораторной работы № 11 воспользуйтесь уже известным Вам приложением NMM_Labs.

Выберите требуемую лабораторную работу и свой вариант. После этого – нажмите на кнопку «Выполнить» – перед Вами появится следующая форма:

Пользователю предоставляется возможность вычислять значение для таблично заданной функции, а также ее производной, при помощи одного из двух интерполяционных многочленов. Выбор многочлена производится путем «включения» соответствующей радио-кнопки из группы «Интерполяционный многочлен».

Напомним, что вводимое значение аргумента должно быть в пределах отрезка интерполирования.

Кроме того, Вы можете задать другое «Количество интервалов основной таблицы», например – 25, которое при начальной загрузке имеет минимальное значение – 20.

Для исследования влияния степени многочлена на относительную погрешность вычисления Вы можете увеличивать этот параметр (от 4 до 9).

После того, как выбран интерполяционный многочлен, например – Лагранжа, и задано конкретное значение аргумента, необходимо нажать на кнопку «Вычислить значение функции и ее производной»:

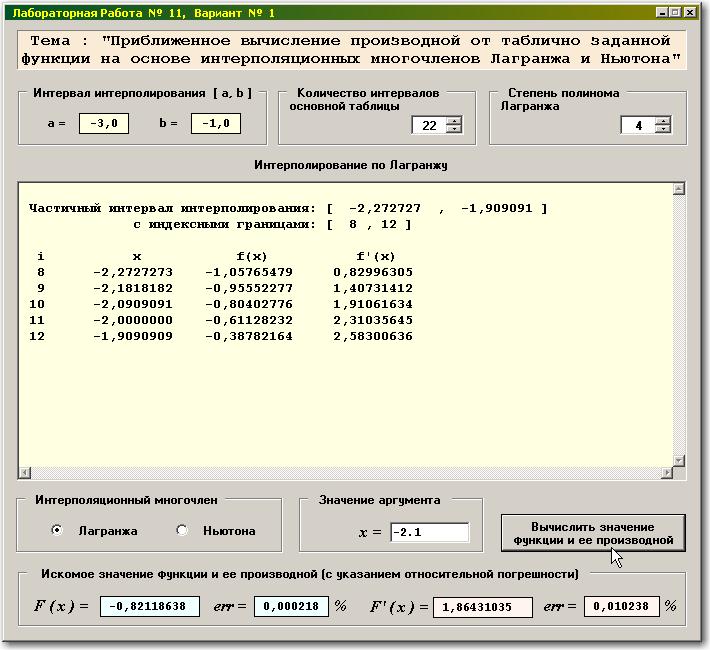
Основной результат интерполирования размещается внизу формы.

Для наглядности работы данного расчетного алгоритма (интерполирования по Лагранжу), а также для облегчения отладки Вашей программы, выводится таблица функции и ее производной, рассчитанные по аналитическим формулам.

Если же был выбран многочлен Ньютона, то форма с результатами будет иметь вид:

Здесь также выводится дополнительная информация, раскрывающая особенности интерполирования по Ньютону, и позволяющая производить отладку подобной программы.

Вам следует выполнить ряд вычислений для различных значений аргумента и для обоих методов интерполирования, чтобы убедиться в корректности работы Вашей программы по данной лабораторной работе.

Работа считается выполненной, если результаты, полученные Вашей программой для значений аргумента из «верхней», «средней» и «нижней» частей расчетных таблиц (файлов Table_dy.txt или LabTask_11с.txt) совпадут с результатами программы NMM_Labs.

Дата добавления: 2014-12-23