Общие указания

Курск 2002

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ

М ышления

Т ворческого

И ндивидуального

Р азвитие

ЖЕЛАЮ ВАМ УСПЕХА И УДАЧИ В ДАЛЬНЕЙШИХ ЗАРАОТКАХ!!!

Индивидуальные задания к модулю №15.1

Составители: Е.А.БОЙЦОВА, В.И.ДРОЗДОВ

УДК 510(083)

Рецензент:

Кандидат физико-математических наук, доцент кафедры высшей математики.Дмитриев В.И

Операционное исчисление. Методические указания к выполнению модуля 15.1/ Курск. гос. техн. ун.-т; Сост. Е.А Бойцова., В.И. Дроздов. Курск, 2002. 26 с.

Работа предназначена для студентов всех специальностей.

Библиогр. 6 назв.

Текст печатается в авторской редакции

ИД № 06430 от 10.12.2001. ПЛД № 50-25 от 1. 04. 97.

Подписано в печать. Формат 60х84 1/16. Печать офсетная.

Усл. печ. л. 0,56. Уч. изд. л.0,52. Тираж 100 экз. Заказ. Курский государственный технический университет.

Издательско-полиграфический центр Курского государственного технического университета. 305040 г. Курск, ул. 50 лет Октября, 94.

СОДЕРЖАНИЕ

Общие указания……………………………………………………… 4

Общие теоретические положения……………………….…………...4

Теоретические вопросы………………………………………………8

Задание №1…………………………………………………………..9

Задание №2…………………………………………………………..9

Задание №3………………………………………………………… 15

Задание №4………………………………………………………… 18

Задание №5………………………………………………………… 20

Примеры выполнения заданий……………………………………..23

Библиографический список……………………………………….. 26

Настоящее пособие предназначено для студентов, изучающих курс операционного исчисления и работающих в системе «Ритм». Оно содержит теоретические вопросы, теоретические упражнения и расчетные задания к модулю 15.1 – «Операционное исчисление». Самостоятельное выполнение этих заданий послужит закреплению у студентов умения использовать теорию преобразования Лапласа в прикладных вопросах высшей математики.

Теоретические сведения по данному разделу курса высшей математики см. в работах [1,3,4,5].

ОБЩИЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Определение. Любая комплексная функция f (t) действительного аргумента t называется оригиналом, если она удовлетворяет следующим условиям:

1) f (t) – кусочно-непрерывная функция, т.е. на любом конечном отрезке имеет лишь конечное число точек разрыва 1-го рода;

2) f (t)=0 при t <0;

3) f (t) – функция ограниченного роста, т. е. существуют такие постоянные M >0 и s, что для всех t выполняется соотношение

| f (t) |< М×е^st (1)

Нижняя грань s ₀ всех чисел s, для которых справедливо неравенство (1), называется показателем роста функции f (t).

Простейшей функцией-оригиналом является так называемая единичная функция Хевисайда:

Очевидно, умножение функции j (t) на h (t) “гасит” эту функцию при t <0 и оставляет без изменения при при t ³0, т. е.

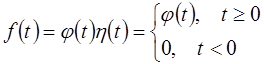
Определение. Изображением функции f (t) (по Лапласу) называется функция комплексного переменного p=s+is, определяемая соотношением:

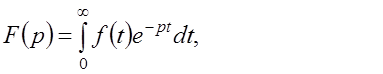(2)

где интеграл берется по положительной полуоси. Фразу “функция f (t) имеет своим изображением F (p)” будем записывать символом:

f (t) ÷ F (p) или F (p) ÷ f (t).

Теорема 1. Для всякого оригинала f (t) изображение F (p) определено в полуплоскости Re p>s ₀, где s ₀ - показатель роста для f (t), и является в этой полуплоскости аналитической функцией.

Теорема 2. Если функция f является оригиналом и F (p) служит ее изображением, то в любой точке t, в которой функция f непрерывна, справедливо равенство:

(3)

где интеграл берется вдоль любой прямой Re p=а>s ₀ и понимается в смысле главного значения, т. е. как предел интеграла вдоль отрезка [ a-ib; a+ib ] при b ®¥.

Теорема 3. Оригинал f (t) вполне определяется своим изображением F (p) с точностью до значений в точках разрыва f (t).

Теорема разложения. Пусть функция F (p):

1) мероморфна и правильна в некоторой полуплоскости Re p>s ₀;

2) существует система окружностей С_п: | p |< R_n, R ₁< R ₂<…< R_n ®¥, на которой F (p) стремится к нулю равномерно относительно arg p;

3) для любого а > s ₀ абсолютно сходится интеграл Тогда оригиналом F (p) служит (умноженная на h (t)) функция

(4)

где сумма вычетов берется по всем особым точкам р_k функции F (p) в порядке неубывания их модулей.

1. Свойство линейности. Для любых (комплексных) постоянных a и b: a×f (t)+ b×g (t)¸ a×F (p)+ b×G (p).

2. Теорема подобия. Для любого постоянного a >0

(5)

3. Дифференцирование оригинала. Если функция f (t) непрерывна при t >0 и f’ (t) или вообще f ^(п) (t) является оригиналом, то

f’ (t) ÷ pF (p)- f (0) (6)

или

f ^(п) (t) ÷ pⁿF (p)- p^n-1f (0)- p^n-2f¢ (0)-…- f ^(n-1) (0), (7)

где под f ^k (0) понимается правое предельное значение .

4. Дифференцирование изображения: Дифференцирование изображения сводится к умножению на – t оригинала, или вообще

F^(п) (p) ÷ (-1) ^пtⁿf (t). (8)

5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р

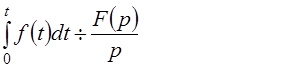(9)

6. Интегрирование изображения. Если интеграл сходится, то он служит изображением функции f (t)/ t:

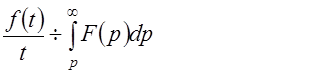(10)

(интегрирование изображения равносильно делению на t оригинала).

7. Теорема запаздывания. Для любого положительного t

f (t-t) ÷ е^-рt×F (p) (11)

(включение оригинала с запаздыванием на t равносильно умножению изображения на е^-рt).

8. Теорема опережения. Для любого положительного t

(12)

9. Теорема смещения. Для любого комплексного р ₀

× f (t) ÷ F (p-p ₀) (13)

(“смещение” изображения на р ₀ равносильно умножению оригинала на ).

10. Теорема умножения (Э. Борель) (или теорема о свертке). Произведение двух изображений F (p) и G (p) является изображением, причем

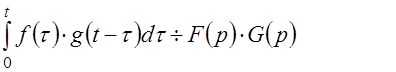(14)

Дата добавления: 2014-12-24