
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интеграл Дюамеля. 2 страница
|
|
|
|
Задание 4. Операционным методом решить дифференциальные уравнения, удовлетворяющие заданным начальным условиям:
| 4.1 | 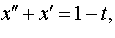 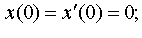
| 4.2 | 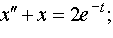 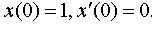
|
| 4.3 | 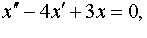 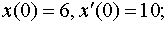
| 4.4 | 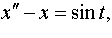 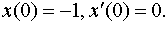
|
| 4.5 | 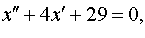 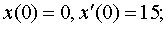
| 4.6 | 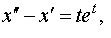 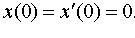
|
| 4.7 | 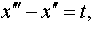 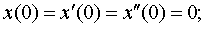
| 4.8 | 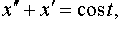 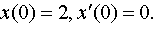
|
| 4.9 | 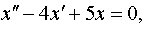 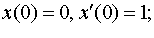
| 4.10 | 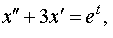 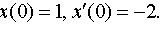
|
| 4.11 | 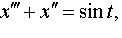 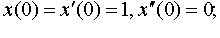
| 4.12 | 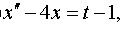 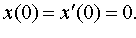
|
| 4.13 | 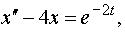 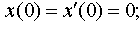
| 4.14 | 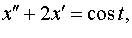 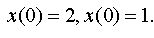
|
| 4.15 | 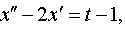 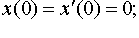
| 4.16 | 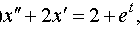 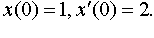
|
| 4.17 | 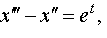 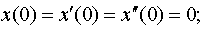
| 4.18 | 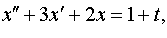 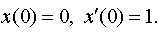
|
| 4.19 | 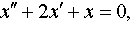 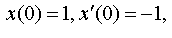
| 4.20 | 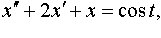 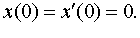
|
| 4.21 | 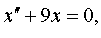 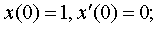
| 4.22 | 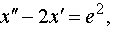 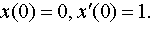
|
| 4.23 | 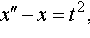 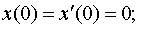
| 4.24 | 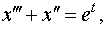 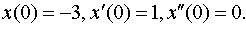
|
| 4.25 | 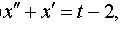 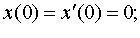
| 4.26 | 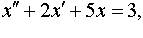 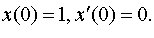
|
| 4.27 | 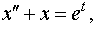 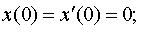
| 4.28 | 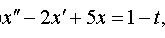 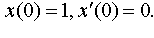
|
| 4.29 | 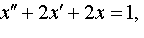 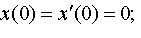
| 4.30 | 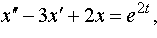 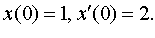
|
| 4.31 | 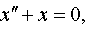 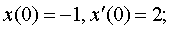
| 4.32 | 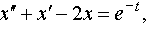 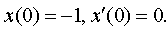
|
| 4.33 | 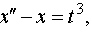 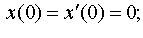
| 4.34 | 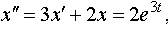 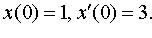
|
| 4.35 | 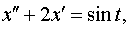 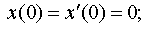
| 4.36 | 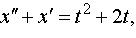 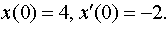
|
| 4.37 | 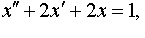 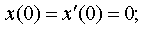
| 4.38 | 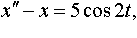 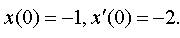
|
| 4.39 | 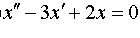 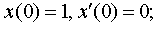
| 4.40 | 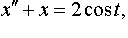 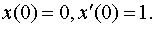
|
| 4.41 | 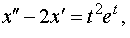 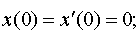
| 4.42 | 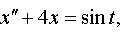 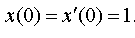
|
| 4.43 | 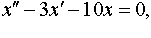 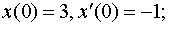
| 4.44 |  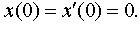
|
| 4.45 | 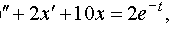 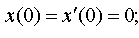
| 4.46 | 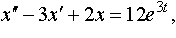 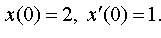
|
| 4.47 | 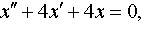 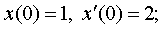
| 4.48 | 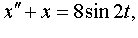 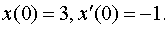
|
| 4.49 | 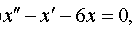 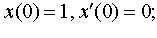
| 4.50 | 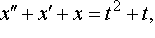 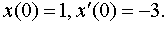
|
Задание 5. Решить систему дифференциальных уравнений:
5.1. 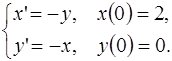 5.2.
5.2. 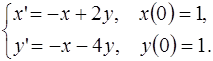
5.3. 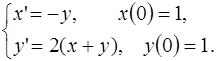 5.4.
5.4. 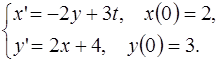
5.5. 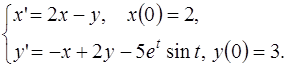 5.6.
5.6. 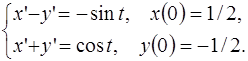
5.7. 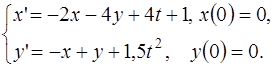 5.8.
5.8. 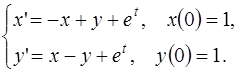
5.9. 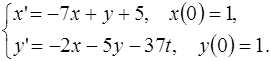 5.10.
5.10. 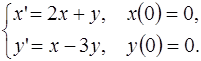
5.11. 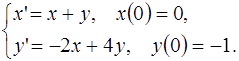 5.12.
5.12. 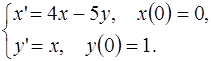
5.13. 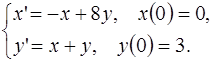 5.14.
5.14. 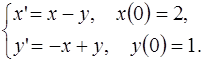
5.15. 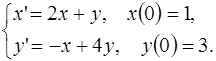 5.16.
5.16. 
5.17. 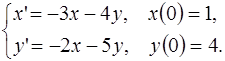 5.18.
5.18. 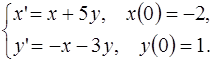
5.19. 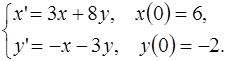 5.20.
5.20. 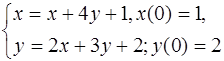
5.21. 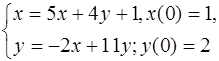 5.22.
5.22. 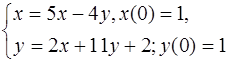
5.23. 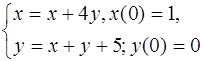 5.24.
5.24. 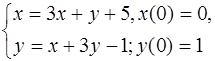
5.25. 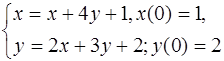 5.26.
5.26. 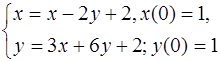
5.27. 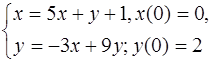 5.28.
5.28. 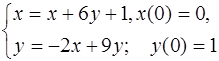
5.29. 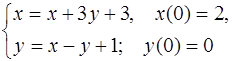 5.30.
5.30. 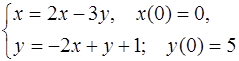
5.31. 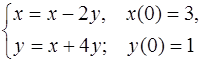 5.32.
5.32. 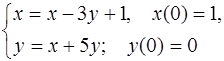
5.33. 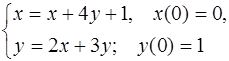 5.34.
5.34. 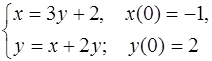
5.35. 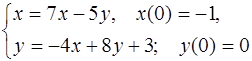 5.36.
5.36. 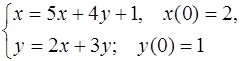
5.37. 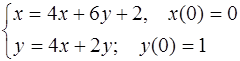 5.38.
5.38. 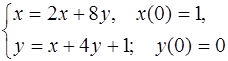
5.39. 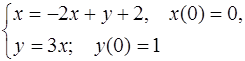 5.40.
5.40. 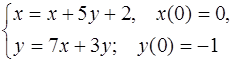
5.41. 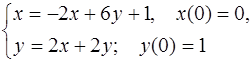 5.42.
5.42. 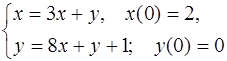
5.43. 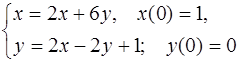 5.44.
5.44. 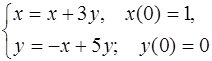
5.45. 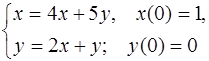 5.46.
5.46. 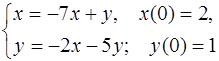
5.47. 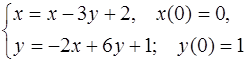 5.48.
5.48. 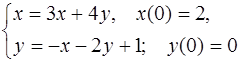
5.49. 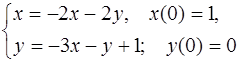 5.50.
5.50. 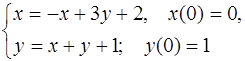
ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАЧ
Пример 1: Пользуясь определением, найти изображение функции е2t.
Решение: В силу формулы (2) имеем
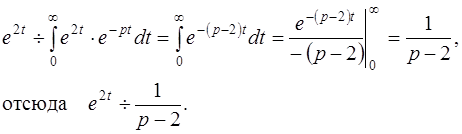
Пример 2: Найти изображение функции е2tsin 7 t.
Решение: Применяя формулу 9 из таблицы изображений при a =2, b =7, будем иметь
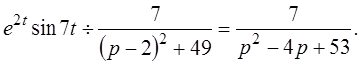
Пример 3: Найти изображение функции
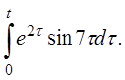
Решение: Воспользуемся свойством интегрирования оригинала и результатом решения предыдущего примера, будем иметь
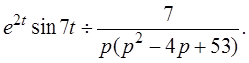
Пример 4: Найти изображение функции
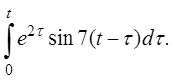
Решение: Т. к. 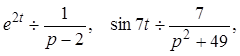 то в силу теоремы о свертке (см. (14)) будем иметь
то в силу теоремы о свертке (см. (14)) будем иметь

Пример 5: Найти изображение функции
е2tsin 7(t- 3)× h (t- 3).
Решение: Преобразуем выражение так, чтобы можно было воспользоваться теоремой запаздывания
е2t × sin 7(t- 3)× h (t- 3)= е6 × е2(t-3) × sin 7(t- 3)× h (t- 3)¸
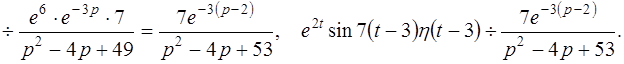
Пример 6: Найти изображение функции
(t2 +1) е-t.
Решение: Используя свойство линейности и формулы 2 и 8 в таблице изображений, получим
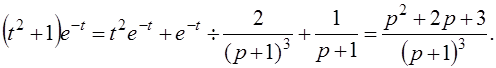
Пример 7: Найти оригинал функции
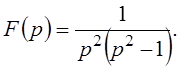
Решение: Представим данную дробно-рациональную функцию в виде суммы простейших дробей:
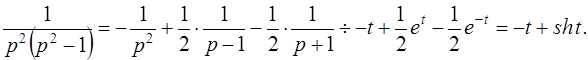
Здесь мы воспользовались формулами 2 и 3 из таблицы оригиналов.
Операционный метод особенно просто применяется к решению линейных дифференциальных уравнений с постоянными коэффицентами и систем таких уравнений. Рассмотрим это на конкретном примере.
Пример 8: Решить дифференциальное уравнение х²+х¢=е 2 t.
Решение: Пусть x (t)¸ X (p), тогда x¢ (t)¸ рX (p)-1, x¢¢ (t)¸ р 2 X (p)- р- 2, x¢¢¢ (t)¸ р 3 X (p)- р 2 - 2 р- 0 согласно свойству дифференцирования изображения, кроме того, 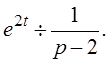 Тогда данное уравнение в изображениях примет вид:
Тогда данное уравнение в изображениях примет вид:
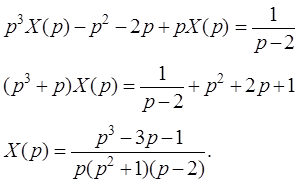
Разложив функцию Х (р) на простейшие дроби с помощью неопределенных коэффициентов, получим
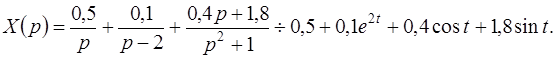
Тогда решение х (t)=0,5+0,1 e 2 t+ 0,4cos t +1,8sin t.
Пример 9: Решить систему
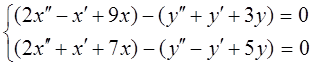
при начальных условиях х (0)= х¢ (0)=1, у (0)= у¢ (0)=0.
Решение: Пусть x (t)¸ X (p), у (t)¸ У (p), тогда x¢ (t)¸ рX (p)-1, x¢¢ (t)¸ р 2 X (p)- р- 1, у¢ (t)¸ рУ (p), у¢¢ (t)¸ р 2 У (p), согласно свойству дифференцирования изображения. Перейдем к операторной системе
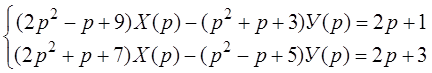
Для упрощения системы найдем сумму и разность ее уравнений:
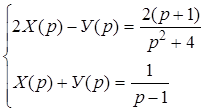 .
.
Отсюда
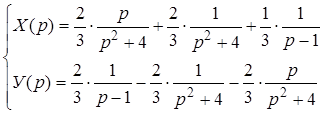 .
.
Переходя к оригиналам, найдем решение
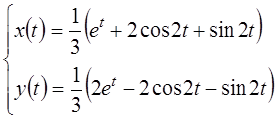 .
.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 497; Нарушение авторских прав?; Мы поможем в написании вашей работы!