Теорема (К.Пирсон, Р.Фишер)

Если верна модель, по которой рассчитаны теоретические частоты Т, то при неограниченном росте числа наблюдений распределение случайной величины X² стремится к распределению хи-квадрат. Число степеней свободы этого распределения определяется как разность между числом событий и числом связей, налагаемых моделью.

В рассматриваемом примере число событий - это число ячеек в таблице сопряженности, то есть число событий вида A_iB_j. Оно равно rs = 4. Связи возникали при подсчёте средних. Число таких независимых соотношений равно r для строк, s - для столбцов, одна связь общая, число степеней свободы распределения хи-квадрат при проверке независимости равно:

rs - (r - 1) - (s - 1) - 1 = (r - l)(s - 1).

Для статистики X² существует другая форма: 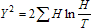только при большом числе наблюдений n. Считается достаточным, чтобы по всем ячейкам теоретические частоты были бы не меньше 5. Есть данные, что это ограничение в задаче независимости признаков можно снизить до 3, так что должно выполняться соотношение: n_i. n_.j /n > 3. Требования к ожидаемым частотам смягчаются при увеличении числа степеней свободы. Если гипотеза независимости неверна, для зависимых признаков X² неограниченно возрастает при увеличении n. Поэтому большие значения X² указывают на взаимную зависимость признаков. В примере расчет, дает X_н² = 12,6. Число степеней свободы для таблицы 3×3 равно 4. Вычислив: 1,3%, где ρ(х) - плотность распределения 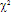(4), находим оценку вероятности того, что наблюдённое (или большее) значение получено случайно. Если пользоваться таблицей верхних процентных точек распределения 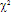(4), то найдём, что X_н² = 9,5 соответствует вероятность 5%, а 13,2 - 1%. Можно считать, что в примере признаки не являются независимыми, связь между ними проявляется. Говорят, что данная таблица значима.

В простейшем частном случае таблиц сопряженности, когда признаки А и В принимают только по 2 значения:

,

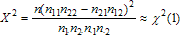рекомендуется модифицированная статистика:

,

Дата добавления: 2014-12-24