Зависимость расходов на потребление от дохода 3 страница

3. ОБРАЗЕЦ ВЫПОЛНЕНИЯ

Исходные данные

Пусть X – личный доход в США (млрд. долларов, в ценах 2000-2011 гг.), Y – персональный расход на потребление в 2000-2011 гг. (табл.2.4)

Таблица 2.4

Годы	Личный доход (Х)	Персональный расход на потребление (Y), млрд. долларов	Годы	Личный доход (Х)	Персональный расход на потребление (Y), млрд. долларов
	7327,1	6830,3			9772,2
	7648,4			11024,5	10035,5
	8009,6	7439,1		10788,8	9866,1
	8376,1	7804,1		11179,6	10245,5
	8887,7	8272,7		11553,2	10724,4
	9277,6	8803,5
	9915,6	9300,9		x *=12000

Данные взяты на сайте https://datamarket.com/data/set/1fsm/us-economic-statistics-disposable-personal-income-seasonally-adjusted-annual-rate#!
https://datamarket.com/data/set/1fs6/us-economic-statistics-personal-consumption-expenditures#!

1. По заданному варианту экспериментальных данных построим корреляционное поле (x_i, y_i), i  = 1,2,…, 12 (см. рис.2.3). На основании визуального исследования выдвинем гипотезу о линейной зависимости Y от X :  Y  =  a + bX + e.

2. Числовые характеристики случайных величин найдем по формулам, приведенным в таблице 1.3.

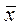 = (1/ n)å x_i  = (1/12)(7327,1 + 7648,4 + … + 11553,2) = 9534,4;

 = (1/ n)å y_i  = (1/12)(6830,3 +7151 + … + 10724,4) = 8853,8;

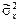 = (1/12)å x_i ²–  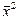= (1/12)((7327,1)² + … + (11553,2)²) – (9534,4)² =2008664,8;

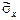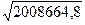=  = 1417,2;

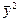 = (1/12)å y_i ²–  = (1/12)((6830,3)² + … + (10724,4)²) – (8853,8)² =  1611909,8;

=  = 1269,6;

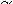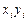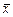
cov(X, Y) = (1/ n)å –  = (1/12)(6830,3 × 7327,1 + … + 10724,4 ×  11553,2)  – 8853,8 × 9534,4 = 1794293,6

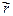 = cov (X, Y) / (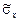 ) = 1794293,6/(1269,6 ×1417,2 ) = 0,99.

3. Оценки коэффициентов уравнения регрессии находим по формулам (2.2):

b  = cov(X, Y)/s _x ² = 1794293,6 / 2008664,8= 0,893

a  =  –  b· 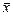 = 8853,8– 0,893 × 9534,4 = 339,5

Уравнение регрессии имеет вид

y = a + b·x  = 339,5 + 0,893· x. (2.4)

4. Рассчитаем по уравнению регрессии значение 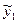и прогнозируемое значение y *:

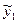 =  a  +  b·x ₁ = 339,5 + 0,893 × 7327,1 = 6882,6,

y *= a + b·x * = 339,5 + 0,893 × 12000 = 11055,5.

Погрешность d₁ =  y ₁ – 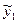 = 6830,3– 6882,6 = -52,3. Относительная погрешность вычисления y ₁ равна 0,7%: d₁/ y ₁ » 0,007.

5. Построим линию регрессии y = a + b·x  = 339,5 + 0,893· x

по двум точкам (x ₁, y ₁) и (x *, y *) (рис.2.1).

6. Коэффициент детерминации r² = R ² =(0.99)²=0.98, что говорит о высоком качестве модели. Действительно, 98% изменчивости расходов Y объясняется влиянием фактора X, остальные 2% -влиянием других факторов.

Критерий проверки гипотезы о значимости уравнения регрессии по критерию Фишера описан в п.1.10. Расчетное значение статистики Фишера определяем по формуле (1.22 ), учитывая, что число факторов модели k=1: F_расч= 0.98·10/(1-0.98) =495.

8. Критическое (табличное) значение статистики Фишера определим по таблице (например, [ 2], табл.А.3) для заданного уровня значимости α =0.05 и числа степеней свободы k=1 и n-k-1=12-1-1=10: F_табл(1, 10)=4.96. Т.к.

F_расч > F_табл, то гипотеза H₀ об отсутствии влияния переменной X на Y отклоняется, а уравнение регрессии (2.4) признается значимым на уровне значимости α =0.05.

Решение с помощью ППП Excel

При использовании в расчетах пакета Excel сначала в первые две колонки файла вводятся исходные денные. Далее можно в соседних колонках вычислить квадраты значений x _i², y _i² и произведение двух столбцов x_i, y_i,

i  = 1, …, n. Проводя суммирование по каждому из полученных пяти столбцов, получим значения å x_i, å y_i, å x_i ², å y_i ², å x_iy_i, по которым непосредственно рассчитываются числовые характеристики из заданий 2 и 3. Фрагмент расчетов для нашего примера приведен в таблице 2.2.

Таблица 2.4

n	X	y	x ^2	Y ^2	xy
	7327,1	6830,3			50046291,1
…	…	…	…	…	…
	11553,1	10724,4
Итого	106245,8	112177,8	960020211		1034519572

По найденным значениям сумм затем, как это сделано выше, проводятся все остальные расчеты.

Гораздо более эффективно задачу о нахождении уравнения линейной регрессии можно решить, используя встроенную функцию ЛИНЕЙН., определяющую параметры линейной регрессии и ряд дополнительных статистик. Для обращения к этой функции:

1) открыть файл, содержащий анализируемые данные (два столбца), и выделить в нем область пустых ячеек 5´2 для вывода результатов анализа;

2) в главном меню выбрать пункт Вставка/Функция, а в нем функцию Статистические/ЛИНЕЙН., и заполнить диалоговое окно ввода переменных (введя информацию о значениях X и Y и две константы 1 и 1);

3) вывести дополнительные статистики можно, нажав клавиши F2, затем Ctrl + Shift + Enter.

Решение с помощью ППП STATGRAPHICS

1. Создайте файл, и в нем занесите ваши данные

(x_i, y_i), i  = 1, …, n, в колонки X и Y соответственно.

2. Для нахождения числовых характеристик случайных величин X и Y откройте окно описательного анализа функций многих переменных Describe\Numeric Data\One Variable Analysys. В нем нажмите кнопку Tabular Options и в диалоговом окне отметьте пункты Summary Statistics и Correlation. Результат появится в виде таблицы, фрагмент которой представлен в табл. 2.5.

Таблица 2.5.

Дата добавления: 2014-12-24